Luogu P5280 [ZJOI2019]线段树

gate

用时：看题解一上午，写代码120min

省选打完了，继续停课...
gg说要做历年省选题，还要看博客...公开处刑...

每个\(modify\)操作会复制1倍线段树并修改。
然而实际上不需要维护那么多线段树，维护1棵并在树上dp即可。
对于不同状态的节点有不同的维护操作，需要分类讨论。

（Linux还没整画图软件，就借用下洛谷题解的图吧...）

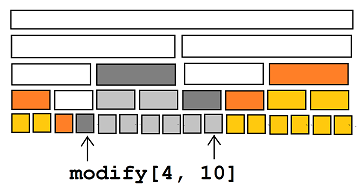
1. （白）包含modify区间
2. （黑）能被遍历，属于modify区间
3. （橙）能被遍历，不属于modify区间
4. （灰）不能被遍历，属于modify区间
5. （黄）不能被遍历，不属于modify区间

设：
\(total\)表示本次modify增加的线段树个数。
\(f[i]\)表示节点\(i\)在所有线段树中，有tag的个数。
\(g[i]\)表示节点\(i\)在所有线段树中，从\(1\)到\(i\)的路径上都没有tag的个数。

1.

由于要向下找区间，所以\(i\)的tag会被pushdown下去。
因此，从\(1\)到\(i\)都一定没有tag。

\[\begin{cases} f[i] += 0\\ g[i] += total \end{cases}\]

2.

modify即在\(i\)上加一个tag，所以一定有tag。

\[\begin{cases} f[i] += total\\ g[i] += 0 \end{cases}\]

3.

\(i\)没有modify，但会被祖先pushdown。
祖先若有tag，pushdown后i也有tag，有tag的个数即为\(tot-g[i]\)；
祖先若没有tag，则直接转移。
这里要注意顺序，先修改f再修改g。

\[\begin{cases} f[i] += total-g[i]\\ g[i] *= 2 \end{cases}\]

4.

\(i\)的祖先被打了tag，但不需要pushdown。
所以\(i\)是否有tag直接转移，但祖先一定有tag。

\[\begin{cases} f[i] *= 2\\ g[i] += 0 \end{cases}\]

5.

\(i\)根本不会被遍历到。直接转移。

\[\begin{cases} f[i] *= 2\\ g[i] *= 2 \end{cases}\]

情况\(1,2,3\)在维护线段树时暴力转移即可；
情况\(4,5\)可以用\(lazy\)标记维护。
在转移\(2\)时给\(4\)打标记，在转移\(3\)时给\(5\)打标记。

初始化：\(f[i]=0, g[i]=1\)。
由于是乘法，\(lazy_f[i] = lazy_g[i] = 1\)

\(sum[i]\)表示\(i\)的子树内有tag的个数。
\(sum[i] = f[i] + sum[ls] + sum[rs]\)
\(sum[1]\)即为答案。

---

注意：

• 变量全部long long。
• 防止RE，数组开\(8\)倍。
• 几乎每个修改前都要先\(pushdown\)，改完要\(pushup\)。
  （我就是在从\(3\)修改\(5\)时，没有先把\(3\) \(pushdown\)，所以WA了）

代码如下

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#define Mogeko qwq
using namespace std;

#define Mid (l+r>>1)
#define ls (now<<1)
#define rs (now<<1|1)

const int maxn = 8e5+10;
const int mod = 998244353;

int n,m,op,x,y;
long long k,f[maxn],g[maxn],lazf[maxn],lazg[maxn],sum[maxn];

int read(){
    int x = 0,f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while('0' <= ch && ch <= '9'){
        x = x*10 + ch-'0';
        ch = getchar();
    }
    return x;
}

void build(int l,int r,int now){
    g[now] = lazf[now] = lazg[now] = 1;
    if(l == r) return;
    int mid = Mid;
    build(l,mid,ls);
    build(mid+1,r,rs);
}

void pushup(int now){
    sum[now] = (f[now] + (sum[ls] + sum[rs]) %mod) %mod;
}

void push_f(int now,long long x){
    (f[now] *= x) %= mod;
    (lazf[now] *= x) %= mod;
    (sum[now] *= x) %= mod;
}

void push_g(int now,long long x){
    (g[now] *= x) %= mod;
    (lazg[now] *= x) %= mod;
}

void pushdown(int now){
    if(lazf[now] > 1)
        push_f(ls,lazf[now]), push_f(rs,lazf[now]);
    if(lazg[now] > 1)
        push_g(ls,lazg[now]), push_g(rs,lazg[now]);
    lazf[now] = lazg[now] = 1;
}

void upd(int now,int id){
    if(id == 1)
        (g[now] += k) %= mod;
    else if(id == 2){
        (f[now] += k) %= mod;
        push_f(ls,2), push_f(rs,2);      
    } 
    else if(id == 3){
        pushdown(now);
        (f[now] += ((k - g[now]) %mod+mod)%mod) %= mod;
        (g[now] += g[now]) %= mod;
        push_f(ls,2), push_f(rs,2);
        push_g(ls,2), push_g(rs,2);
    }
    pushup(now);
}

void modify(int L,int R,int l,int r,int now){
    pushdown(now);
    if(L == l && R == r){
        upd(now,2);
        return;
    }
    int mid = Mid;
    upd(now,1);
    if(R <= mid){
        modify(L,R,l,mid,ls);
        upd(rs,3);
    }
    else if(L >= mid+1){
        modify(L,R,mid+1,r,rs);
        upd(ls,3);
    }
    else {
        modify(L,mid,l,mid,ls);
        modify(mid+1,R,mid+1,r,rs);
    }
    pushup(now);
}

int main(){
    n = read(),m = read();
    build(1,n,1);
    k = 1;
    while(m--){
        op = read();
        if(op == 1){
            x = read(),y = read();
            modify(x,y,1,n,1);
            (k += k) %= mod;
        }
        if(op == 2)
            printf("%lld\n",sum[1]);
    }
    return 0;
}