CF613D Kingdom and its Cities（虚树模板）

gate
这是一道虚树的模板题。首先来介绍一下什么是虚树。

虚树，顾名思义，是一棵原本不存在的树。
虚树DP的标志是：一棵\(n\)个点的树，给出\(k\)个关键点（\(\sum k<\frac{n}{2}\)），求使这些点互不连通的最小代价。
可以发现，答案只与这些点和他们的\(LCA\)有关。
所以，可以通过建一棵只有这些点和他们的\(LCA\)的树，就可以大幅度降低DP的时间复杂度。

例如，我们只保留这张图上的关键点和它们的\(LCA\)：

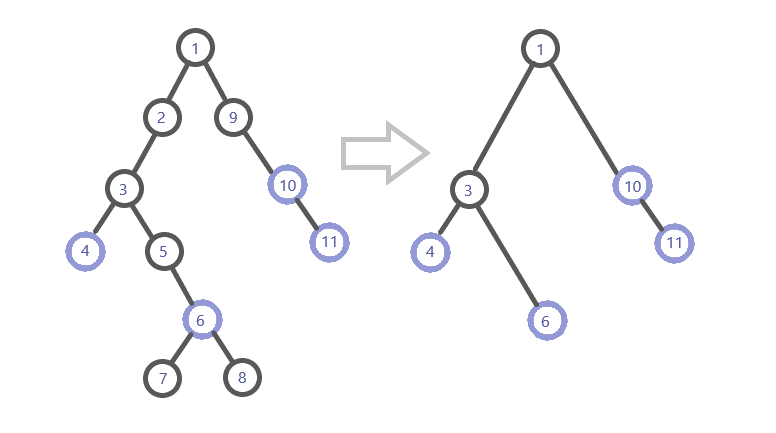
那么，如何建出这个虚树呢？

将关键点按dfs序排序，以符合遍历这棵树的顺序。
维护一个栈，栈中的元素表示从根节点到这个节点的一条链。（处理完所有关键点后，将栈中元素依次连边。）
元素入栈前，要清空这个元素所连的边。
第一个关键点在初始时直接入栈。
假设当前要加入的关键点为new，栈顶元素为top，第二个为top-1，首先求出它们的LCA。
因为按dfs序遍历，因此LCA一定不是new
此时可以分为两种情况：

• \(LCA = top\)：即new在top的子树中（new可以直接入栈）；
• \(LCA \not= top\)：即new和top分别在LCA的两棵子树中。此时要继续讨论：
  检查是否\(dfn[top-1] > dfn[LCA]\)：如果栈顶第二个元素top-1也在LCA的下面，那么top和top-1之间一定需要连边，连完就可以从栈中将top弹出了。
  重复这个过程，直到\(dfn[top-1] ≤ dfn[LCA]\)为止。
  检查LCA是否已在栈中。
  • \(LCA = top-1\)：即LCA已在栈中；则同上连边top和top-1，将top弹出。
  • \(LCA \not= top-1\)：即LCA不在栈中；LCA是为了为了连接top和new的一个新点。因此连接top和LCA，并将LCA入栈。LCA成为了新的top。

处理完这些后，再将new入栈。
（new和LCA入栈前，都不要忘记把边清空！）
如图所示为一个可能的入栈过程：

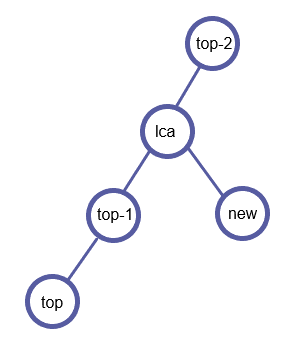
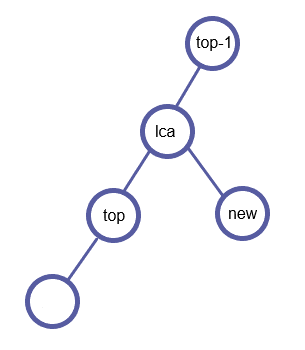
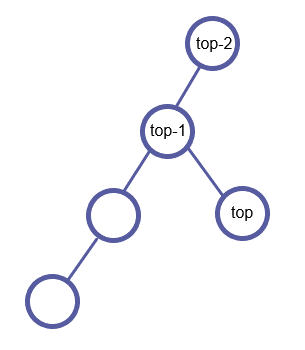
处理完每一个关键点后，将栈中元素依次（i和i+1）连边。

View code

 
void build(int n) {
	st[top = 1] = 1;
	e[1].clear();
	for(int i = 1; i <= n; i++) {
		if(po[i] == 1) continue;
		int lca = getlca(po[i],st[top]);
		if(lca != st[top]) {
			while(dfn[st[top-1]] > dfn[lca])
				add(st[top-1],st[top]),top--;
			if(st[top-1] == lca)
				add(st[top-1],st[top]),top--;
			else {
				e[lca].clear();
				add(lca,st[top]);
				st[top] = lca;
			}
		}
		st[++top] = po[i];
		e[po[i]].clear();
	}
	for(int i = 1; i < top; i++)
		add(st[i],st[i+1]);
}
 

建树完成后就可以开始\(dp\)了。
回到这道题上：求删除最少非关键点使关键点互不连通。
若父子均为关键点，则无解；这里用一个\(vis\)记录该点是不是关键点，检查每个关键点的父亲是否被标记了\(vis\)即可。
设\(f[u]\)表示\(u\)的子树的最小花费，\(g[u]\)表示\(u\)的子树内有多少未断开的关键点。
首先，有\(f[u]=\sum f[v],g[u]=\sum g[v]\)（不包括自己）;

• 若\(u\)是关键点，则\(u\)需要跟它子树中的每个点断开，即\(f[u]+=g[u]\);
  同时，\(u\)本身还没有处理，所以\(g[u] = 1\).
• 若\(u\)不是关键点：
  • 若\(g[u] = 1\)，即\(u\)的子树中只有一个关键点，则没有现在必须处理的点，可以先不操作；
  • 若\(g[u] > 1\)，则去掉\(u\)就可以使子树中的关键点互不连通。此时\(u\)的子树已处理完毕。\(f[u]+=1,g[u]=0\)。

完整代码如下

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#define MogeKo qwq
using namespace std;

const int maxn = 2e5+10;

int n,q,k,now,top,x,y;
int po[maxn],f[maxn],g[maxn],st[maxn];
int dfn[maxn],dpth[maxn],p[maxn][25];
bool vis[maxn];

vector<int> e[maxn];

bool cmp(int x,int y) {
	return dfn[x] < dfn[y];
}

void add(int x,int y) {
	e[x].push_back(y);
	e[y].push_back(x);
}

void dfs(int u,int fa) {
	dfn[u] = ++now;
	dpth[u] = dpth[fa]+1;
	p[u][0] = fa;
	for(int i = 1; (1<<i) <= dpth[u]; i++)
		p[u][i] = p[p[u][i-1]][i-1];
	for(int i = 0; i < e[u].size(); i++) {
		int v = e[u][i];
		if(v == fa) continue;
		dfs(v,u);
	}
}

int getlca(int a,int b) {
	if(dpth[a] < dpth[b])
		swap(a,b);
	for(int i = 20; i >= 0; i--)
		if(dpth[a]-(1<<i) >= dpth[b])
			a = p[a][i];
	if(a == b)return a;
	for(int i = 20; i >= 0; i--)
		if(p[a][i] != p[b][i]) {
			a = p[a][i];
			b = p[b][i];
		}
	return p[a][0];
}

void build(int n) {
	st[top = 1] = 1;
	e[1].clear();
	for(int i = 1; i <= n; i++) {
		if(po[i] == 1) continue;
		int lca = getlca(po[i],st[top]);
		if(lca != st[top]) {
			while(dfn[st[top-1]] > dfn[lca])
				add(st[top-1],st[top]),top--;
			if(st[top-1] == lca)
				add(st[top-1],st[top]),top--;
			else {
				e[lca].clear();
				add(lca,st[top]);
				st[top] = lca;
			}
		}
		st[++top] = po[i];
		e[po[i]].clear();
	}
	for(int i = 1; i < top; i++)
		add(st[i],st[i+1]);
}

void dp(int u,int fa) {
	f[u] = g[u] = 0;
	for(int i = 0; i < e[u].size(); i++) {
		int v = e[u][i];
		if(v == fa) continue;
		dp(v,u);
		f[u] += f[v];
		g[u] += g[v];
	}
	if(vis[u]) {
		f[u] += g[u];
		g[u] = 1;
	} else if(g[u] > 1) {
		f[u]++;
		g[u] = 0;
	}
}

int main() {
	scanf("%d",&n);
	for(int i = 1; i < n; i++) {
		scanf("%d%d",&x,&y);
		add(x,y);
	}
	dfs(1,0);
	scanf("%d",&q);
	while(q--) {
		memset(vis,0,sizeof(vis));
		scanf("%d",&k);
		for(int i = 1; i <= k; i++) {
			scanf("%d",&po[i]);
			vis[po[i]] = true;
		}
		bool flag = false;
		for(int i = 1; i <= k; i++)
			if(vis[p[po[i]][0]]) {
				printf("-1\n");
				flag = true;
				break;
			}
		if(flag) continue;
		sort(po+1,po+k+1,cmp);
		build(k);
		dp(1,0);
		printf("%d\n",f[1]);
	}
	return 0;
}