动态规划问题基础
关于dp问题的一些汇总( ´▽`)
一、线型dp
就是普通的dp啊..
像最大上升子序列,最长公共子序列(LCS)都用到了这种思想w
二、背包型dp
具体参考背包九讲吧qwq
常用的大概就01背包,完全背包,多重背包,有依赖的背包( Luogu P1064 金明的预算方案)...
01背包和完全背包的区别就在于空间的枚举顺序,倒序枚举可以防止重复拿同一个物品。
//01背包 for(int i = 1;i <= n;i++) for(int j = m;j >= 1;j--) f[j] = max(f[j],f[j-c[i]]+w[i]); //完全背包 for(int i = 1;i <= n;i++) for(int j = 1;j <= m;j++) f[j] = max(f[j],f[j-c[i]]+w[i]);
(话说金明这道题我用的是枚举每个空间然后tle了....看到题解是枚举四种情况emmm....)

#include<cstdio>
#include<iostream>
using namespace std;
const int maxn = 32000,subm = 100;
int sum[subm][maxn];
int head[subm],to[subm],next[subm],c[subm],val[subm];
int n,m,v,p,q,cnt;
int add(int i,int v,int p,int q) {
c[i] = v;
val[i] = v*p;
to[++cnt] = i;
next[cnt] = head[q];
head[q] = cnt;
}
void dfs(int x,int fa) {
sum[x][c[x]] = val[x];
for(int i = head[x]; i; i = next[i]) {
int t = to[i];
dfs(t,x);
for(int j = n-c[fa]; j >= c[x]+c[t]; j--)
for(int k = j-c[x]; k >= c[t]; k--)
sum[x][j] = max(sum[x][j],sum[x][j-k]+sum[t][k]);
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i = 1; i <= m; i++) {
scanf("%d%d%d",&v,&p,&q);
add(i,v,p,q);
}
dfs(0,-1);
printf("%d",sum[0][n]);
return 0;
}
但是我觉得这种思想是比较有普遍性的!可以适用于一般的树形dp↓
三、树型dp
就是由下到上在树上dp;
Luogu P2014 选课,P2015 二叉苹果树都是比较经典的树形背包,循环为父亲空间→儿子空间;
状态转移方程:
for(int i = m; i > 1; i--) //m为总容量
for(int j =i-1; j >= 1; j--)
sum[u][i] = max(sum[u][i],sum[u][i-j]+sum[v][j]);

#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int maxn = 305; int n,m,cnt; int a,b; int sum[maxn][maxn]; int head[maxn],to[maxn],next[maxn],val[maxn]; void add(int x,int y,int z) { to[++cnt] = y; next[cnt] = head[x]; head[x] = cnt; val[y] = z; } void dfs(int u,int fa) { for(int i = head[u]; i; i = next[i]) { int v = to[i]; if(v == fa)continue; sum[v][1] = val[v]; dfs(v,u); for(int j = m+1; j > 1; j--) for(int k =j-1; k >= 1; k--) sum[u][j] = max(sum[u][j],sum[u][j-k]+sum[v][k]); } } int main() { scanf("%d%d",&n,&m); for(int i = 1; i <= n; i++) { scanf("%d%d",&a,&b); add(a,i,b); } dfs(0,0); printf("%d ",sum[0][m+1]); return 0; }
Luogu P1352 没有上司的舞会,P2016 战略游戏都是选父亲不选儿子的(应该说是比较简单的类型...)

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 2005;
int n,k,u,v,cnt;
int f[maxn],g[maxn];
int head[maxn],to[maxn],nxt[maxn];
void add(int x,int y){
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x){
for(int i = head[x];i;i = nxt[i]){
int t = to[i];
dfs(t);
f[x] += min(f[t],g[t]);
g[x] += f[t];
}
}
int main() {
scanf("%d",&n);
for(int i = 1; i <= n; i++) {
scanf("%d%d",&u,&k);
for(int j = 1; j <= k; j++) {
scanf("%d",&v);
add(u,v);
}
}
for(int i = 0;i < n;i++){
f[i] = 1;
g[i] = 0;
}
dfs(0);
printf("%d",min(f[0],g[0]));
return 0;
}
Luogu P2458 保安站岗就更复杂一点了...一个节点可以眺望到相邻的节点,这时就需要讨论自己/父亲/儿子三种情况,
难点是,因为一个节点会对它的兄弟造成影响,显然不是无后效性的操作,所以在讨论选儿子的情况时需要把所有儿子都枚举一遍后,
选择由不选变为选的状态,增加量最小的儿子。

#include<cstdio>
#include<iostream>
#define MogeKo qwq
using namespace std;
const int maxn = 2005*2;
const int INF = 2147483647;
int n,k,u,v,cnt;
int f[maxn][3],head[maxn],to[maxn],nxt[maxn];
void add(int x,int y) {
to[++cnt] = y;
nxt[cnt] = head[x];
head[x] = cnt;
}
void dfs(int x,int fa) {
int d = INF;
for(int i = head[x]; i; i = nxt[i]) {
int t = to[i];
if(t == fa)continue;
dfs(t,x);
f[x][2] += min(min(f[t][0],f[t][1]),f[t][2]);
f[x][0] += min(f[t][1],f[t][2]);
f[x][1] += min(f[t][1],f[t][2]);
d = min(d,f[t][2]-min(f[t][1],f[t][2]));
}
f[x][1]+=d;
}
int main() {
scanf("%d",&n);
for(int i = 1; i <= n; i++) {
scanf("%d",&u);
scanf("%d%d",&f[u][2],&k);
for(int j = 1; j<= k; j++) {
scanf("%d",&v);
add(u,v);
add(v,u);
}
}
dfs(1,0);
printf("%d",min(f[1][2],f[1][1]));
return 0;
}
四、区间型dp
区间型dp一般适用于相邻的对象每次操作都会影响结果的问题,主要思想是枚举每个小区间和断点,最后合并成大区间。
一般是n^3的复杂度,循环顺序是长度→起点(终点)→断点;
状态转移方程:
for(int len=2; len<=n; len++) //区间长度
for(int i=1; i<=n; i++) { //枚举起点
int j = i+len-1; //区间终点
if(j>n) break; //判断越界
for(int k=i; k<j; k++) //枚举分割点
dp[i][j] = max(dp[i][j],dp[i][k]+dp[k+1][j]+w[i][j]);
}
Luogu P1063 能量项链,P1880 [NOI1995]石子合并都是区间dp的板子题...
石子合并需要注意:因为每次合并是要加上两部分的总和,所以这时用前缀和就非常方便w

#include<cstdio> #include<algorithm> using namespace std; const int maxn = 305,INF = 2147483647; int n,ans1,ans2,a[maxn],f[maxn][maxn],g[maxn][maxn]; int main(){ scanf("%d",&n); for(int i = 1;i <= n;i++){ scanf("%d",&a[i]); a[i+n] = a[i]; } for(int i = 1;i <= 2*n;i++) a[i] += a[i-1]; for(int l = 1;l < n;l++) for(int i = 1;i+l <= 2*n;i++){ int j = i+l; f[i][j] = 0; g[i][j] = INF; for(int k = i;k < j;k++){ f[i][j] = max(f[i][j],f[i][k]+f[k+1][j]+a[j]-a[i-1]); g[i][j] = min(g[i][j],g[i][k]+g[k+1][j]+a[j]-a[i-1]); } } ans1 = 0; ans2 = INF; for(int i = 1;i <= n;i++){ ans1 = max(ans1,f[i][i+n-1]); ans2 = min(ans2,g[i][i+n-1]); } printf("%d\n%d",ans2,ans1); return 0; }
五、坐标型dp
坐标型dp适用于知道每个物品与不同的选择的对应关系,并且选择需要是单调不能回头的。
形象地说,就像在一张表格中走出一条权值最大的路。
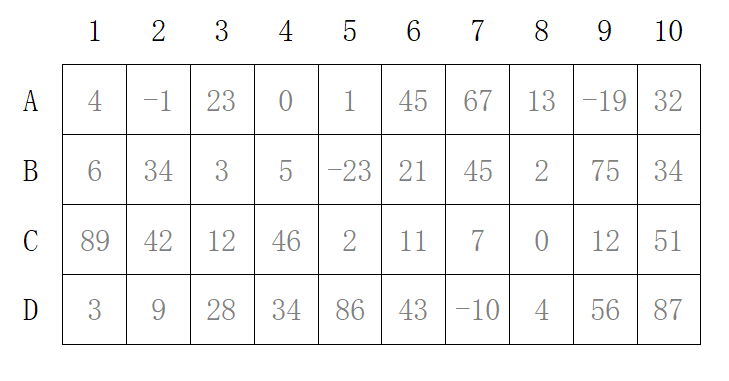
随便走一条路:
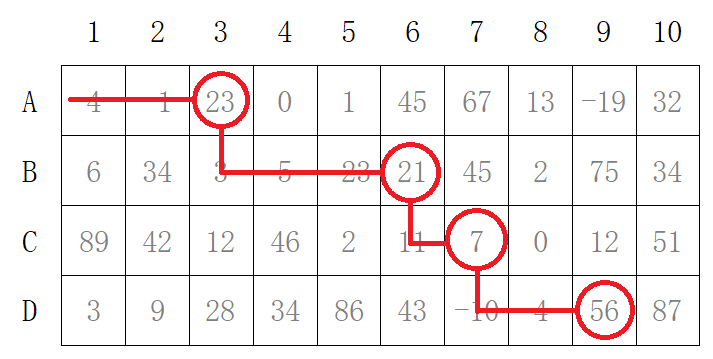
那么这条路径是如何确定的呢?
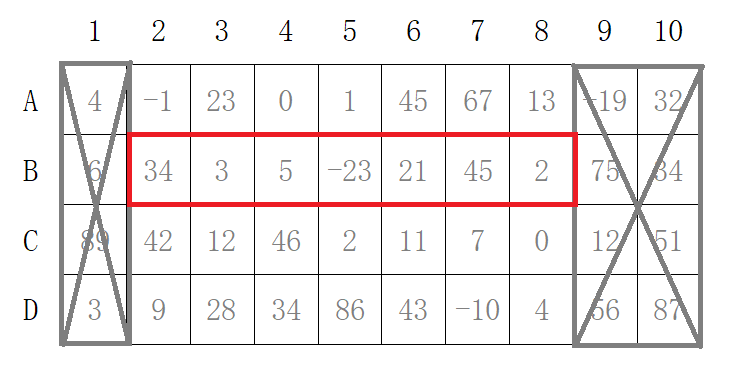
假设走到了第二列,需要给B选择。可选的区间为2~8,因为至少要给前面的A留一个,后面的C、D留两个,即为(int j = i; v-j >= u-i; j++)

比如枚举到(B,6),此时要从它的祖先(即A行)中比它列数小的(1~5)中选择最优解。
状态转移方程:
for(int i = 1; i <= u; i++) //枚举行数(A~D物品)
for(int j = i; v-j >= u-i; j++) //枚举列数
for(int k = i-1; k <= j-1; k++) //枚举祖先
if(f[i][j] < f[i-1][k]+a[i][j])
f[i][j] = f[i-1][k]+a[i][j];
Luogu P1854 花店橱窗布置,P1006 传纸条都是比较经典的例题,
花店橱窗布置需要输出路径,所以要开一个last数组,在枚举祖先的同时记录;
传纸条是一来一回且路径不能重复,所以可以同时枚举两条路径的坐标。因为是同步移动的,所以知道了i1、j1、i2就能算出j2,开三重循环就可以了。

#include<cstdio> #define MogeKo qwq using namespace std; const int maxn = 105; const int INF = 2147483647; int u,v,rslt; int a[maxn][maxn],f[maxn][maxn],last[maxn][maxn],ans[maxn]; int main() { scanf("%d%d",&u,&v); for(int i = 1; i <= u; i++) for(int j = 1; j <= v; j++) { scanf("%d",&a[i][j]); f[i][j] = -INF; } for(int j = 1; j <= v; j++) f[1][j] = a[1][j]; for(int i = 1; i <= u; i++) for(int j = i; v-j >= u-i; j++) for(int k = i-1; k <= j-1; k++) if(f[i][j] < f[i-1][k]+a[i][j]) { f[i][j] = f[i-1][k]+a[i][j]; last[i][j] = k; } rslt = -INF; int k; for(int j = u; j <= v; j++) if(rslt < f[u][j]) { rslt = f[u][j]; k = j; } for(int i = u; i >= 1; i--) { ans[i] = k; k = last[i][k]; } printf("%d\n",rslt); for(int i = 1; i <= u; i++) printf("%d ",ans[i]); return 0; }

#include<cstdio>
#include<iostream>
#define MogeKo qwq
using namespace std;
const int maxn = 105;
int n,m,ans,a[maxn][maxn],f[maxn][maxn][maxn];
int main(){
scanf("%d%d",&m,&n);
for(int i = 1;i <= m;i++)
for(int j = 1;j <= n;j++)
scanf("%d",&a[i][j]);
for(int i1 = 1;i1 <= m;i1++)
for(int j1 = 1;j1 <= n;j1++)
for(int i2 = 1;i2 <= m;i2++){
int j2 = i1+j1-i2;
if(i1 == i2 && j1 == j2 && (i1!=1 || j1!=1))continue;
f[i1][j1][i2] = max(max(f[i1-1][j1][i2-1],f[i1][j1-1][i2-1]),max(f[i1-1][j1][i2],f[i1][j1-1][i2]));
f[i1][j1][i2]+=(a[i1][j1]+a[i2][j2]);
ans = max(ans,f[i1][j1][i2]);
}
printf("%d",ans);
return 0;
}
我个人感觉坐标dp是刚开始学比较难理解的一个地方qwq
六、单调队列优化dp
Luogu P1725琪露诺
因为题解咕了太久我都忘了( ´▽`)

#include<cstdio> #include<iostream> #define MogeKo qwq using namespace std; const int maxn = 1000005; int n,l,r,a[maxn],ans; int q[maxn],num[maxn],head,tail; int main() { scanf("%d%d%d",&n,&l,&r); for(int i = 0; i <= n; i++) scanf("%d",&a[i]); head = 1,tail = 0; for(int i = l; i <= n; i++) { while(head <= tail && q[i-l] >= q[num[tail]])tail--; num[++tail] = i-l; while(num[head] < i-r)head++; q[i] = q[num[head]]+a[i]; if(i>=n-r+1)ans = max(ans,q[i]); } printf("%d",ans); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号