HihoCoder String Matching Content Length
原题链接 http://hihocoder.com/problemset/problem/1059
问题:给定两个字符串A和B,求解A和B的所有公共子串的最大总长度,满足:
1)子串的长度都至少为3;
2)子串的起始位置是单调递增的。
分析:
1)首先可以用矩阵M表示两个字符串的字符匹配情况,其中 M[i][j] 表示将 A[i] 与 B[j] 配对所获得的子串长度,如下图所示:

显然,若 A[i] 与 B[j] 相等,则 M[i][j] = M[i-1][j-1] + 1;否则,M[i][j] = 0。
2)由于每个子串的起始位置是单调递增的,因此A与B的匹配可以划分为两部分M1和M2,如下图所示:
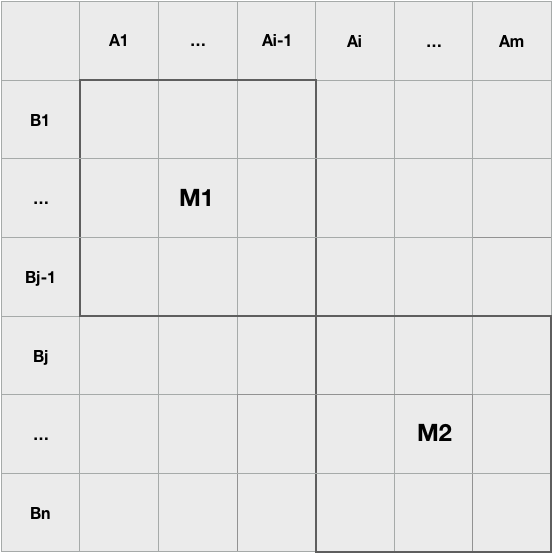
其中,M1为已匹配的部分,即 A[1]...A[i-1] 与 B[1]...B[j-1] 已完成匹配,假设最佳匹配结果为M(i-1, j-1);M2为未匹配的部分,即 A[i]...A[m] 与 B[j]...B[n] 尚未完成匹配。
显然,只需不断扩大M1至M,即可得到问题的最终解。扩展M1有三种可能,如下图所示:
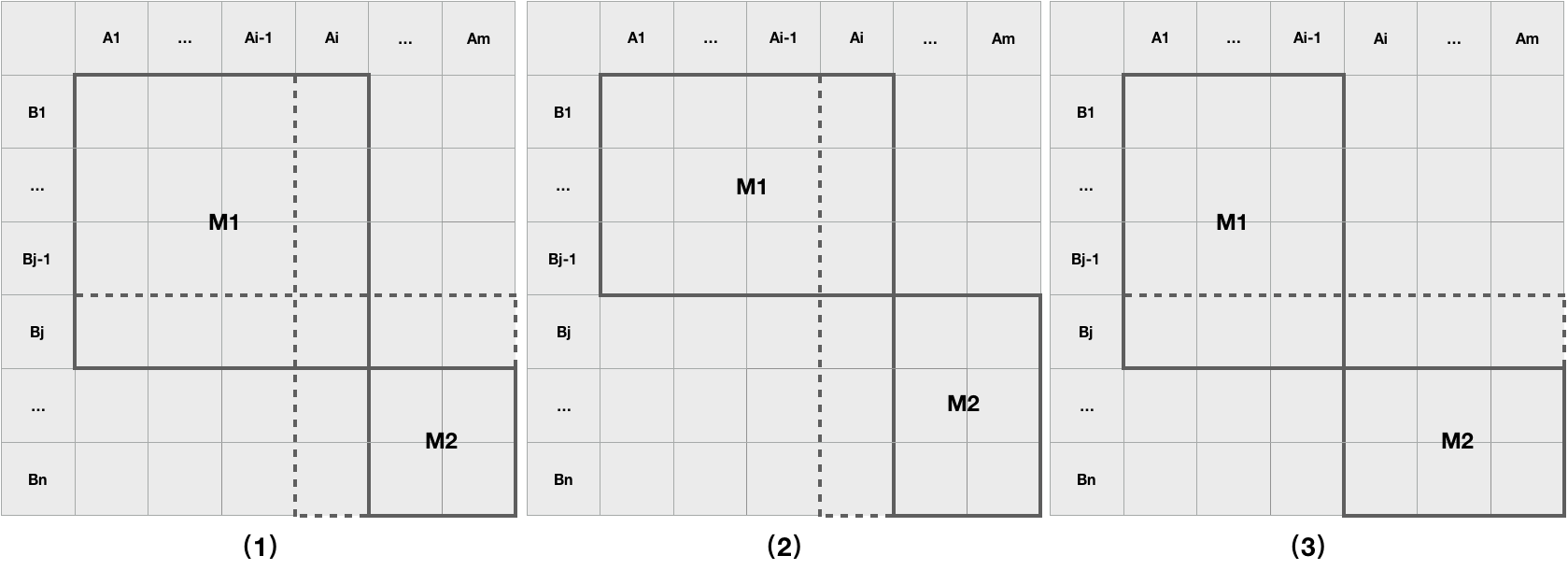
由于场景(2)和场景(3)都可以由场景(1)操作得到,我们只需分析场景(1)即可。当加入 (A[i], B[j]) 时,
若 A[i-k+1]...A[i] 与 B[j-k+1]...B[j] 匹配,且满足长度k大于等于3,则包含该子串的匹配结果为: M(i-k, j-k) + k,取 M(i, j) = max(M(i-k, j-k) + k, M(i-1, j), M(i, j-1)) 即可;
否则, (A[i], B[j]) 加入对匹配结果无影响,取 M(i, j) = max(M(i-1, j), M(i, j-1)) 即可。
显然,求解 M(i, j) 可转化为求解 M(i-k, j-k), M(i-1, j), M(i, j-1),问题规模得以降低。
3)将 M(i, j) 与 M[i][j] 结合起来,M[i][j] 即为 A[i-k+1]...A[i] 与 B[j-k+1]...B[j] 匹配的最大长度K,则 M(i, j) = max(M(i-k, j-k) + k, M(i-1, j), M(i, j-1)),其中 3 <= k <= K。
实际上并不需要遍历所有的k,只需考虑 k = {K,K-1,K-2} 且满足 k >= 3 即可。假设当前匹配为K,M(i-1, j-1) 的最优匹配中与K交叠的匹配为R,如下图所示:

若 K >= 5,当 3 <= k <= K-2,此时R1部分的长度肯定大于等于3,而R2可以由K代替,显然K的匹配长度不小于R2。因此,只需考虑 k = {K,K-1,K-2} 且 k >= 3 即可。
4)只需依次遍历一次M,即可求解该问题。
规则如下:
1)依次遍历M行列。
2)若 A[i] 与 B[j] 相等,则 M[i][j] = M[i-1][j-1] + 1;否则,M[i][j] = 0。
3)若 M[i][j] <= 3,则 M(i, j) = max(M(i-k, j-k) + k, M(i-1, j), M(i, j-1)),其中 max(M[i][j]-2, 3) <= k <= M[i][j];否则,M(i, j) = max(M(i-1, j), M(i, j-1))。
C++代码如下:
1 #include <iostream> 2 #include <string> 3 #include <vector> 4 5 using namespace std; 6 7 struct Node { 8 int total; 9 int curr; 10 Node():total(0), curr(0) {} 11 }; 12 13 class Solution { 14 public: 15 Solution() {} 16 17 void solve() { 18 string A, B; 19 cin >>A >>B; 20 int n = A.length(), m = B.length(); 21 vector<vector<Node> > matrix(n+1, vector<Node>(m+1)); 22 for (int i = 1; i <= n; ++i) { 23 for (int j = 1; j <= m; ++j) { 24 Node &node = matrix[i][j]; 25 node.total = max(matrix[i][j-1].total, matrix[i-1][j].total); 26 if (A[i-1] == B[j-1]) { 27 int curr = node.curr = matrix[i-1][j-1].curr + 1; 28 if (curr < 3) { 29 continue; 30 } 31 for (int k = max(node.curr-2, 3); k <= curr; ++k) { 32 node.total = max(matrix[i-k][j-k].total + k, node.total); 33 } 34 } 35 } 36 } 37 cout <<matrix[n][m].total <<endl; 38 } 39 }; 40 41 int main(int argc, char **argv) { 42 Solution solution; 43 solution.solve(); 44 return 0; 45 }



