HihoCoder 跑马圈地
原题链接 http://hihocoder.com/problemset/problem/1042
问题：在一个m*n的矩形中，圈出一块最大周长为L的连续区域，满足区域面积尽可能大，同时区域边界不能落入内部特定的矩形内。
分析：
1）当周长固定时，围成正方形覆盖的面积最大；
2）考虑到矩形的对称性，内部矩形位置 (阴影区域) 可表示为如下图所示形式，即满足：s1 >= s3 且 s1 >= s2 且 s3 >= s4：
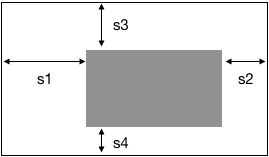
3）除非为了避开阴影区域，否则圈出的区域不需内凹；且圈出区域不会半包裹阴影区域，如下图(1)所示：
4）当L足够长时，圈出区域全部包含阴影区域可获得更大的面积，如下图所示：
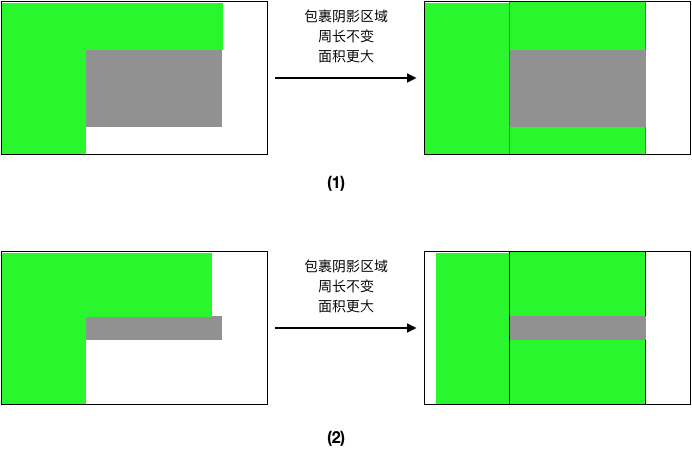
其中，上图中场景(1)显而易见，而场景(2)也是存在的，例如如下输入：
9 15 40 5 12 4 5
正确输出应该是92，而如果输出69，hihoCoder也会AC，应该是平台的测试集有问题。
规则如下：
1）不包含阴影区域，优先圈A1区域，然后圈A2区域，得到S1
2）包含阴影区域，得到S2
3）取S1和S2中较大的值
代码如下：
1 def solve(): 2 n, m, L = (int(x) for x in raw_input().split()) 3 l, r, t, b = (int(x) for x in raw_input().split()) 4 max_hor = max(l, m - r) 5 max_ver = max(t, n - b) 6 # 规范化：使阴影区域位于矩形右下方，且Left >= Top 7 ret = do_solve(m, n, L, max_hor, max_ver, r - l, b - t) if max_hor >= max_ver else \ 8 do_solve(n, m, L, max_ver, max_hor, b - t, r - l) 9 print(ret) 10 11 12 def do_solve(w0, h0, L, l, t, w, h): 13 # 计算包含阴影区域时，所能圈住的最大面积 s1 14 s1 = calc_max_with_block(w0, h0, L, w, h) if w >= h else \ 15 calc_max_with_block(h0, w0, L, h, w) 16 if L >= 2 * (h0 + l + w): 17 return s1 18 else: 19 # 计算不包含阴影区域时，所能圈住的最大面积 s2 20 s2 = calc_max_area(l, h0, L) 21 if L > 2 * (h0 + l): 22 w1 = L // 2 - l - h0 23 s2 += w1 * t 24 return max(s1, s2) 25 26 27 def calc_max_area(w0, h0, L): 28 w = h = min(w0, h0, L // 4) 29 L -= 2 * (w + h) 30 if L <= 1: 31 return w * h 32 if w0 - w > 0: 33 w += min(w0 - w, L // 2) 34 elif h0 - h > 0: 35 h += min(h0 - h, L // 2) 36 return w * h 37 38 39 def calc_max_with_block(w0, h0, L, w, h): 40 L -= 2 * (w + h) 41 if L <= 1: 42 return 0 43 w1 = w 44 h1 = h 45 delta = min(w - h, h0 - h, L // 2) 46 h += delta 47 L -= 2 * delta 48 if L <= 1: 49 return w * h - w1 * h1 50 delta = min(w0 - w, h0 - h, L // 4) 51 w += delta 52 h += delta 53 L -= 4 * delta 54 if L <= 1: 55 return w * h - w1 * h1 56 if w0 - w > 0: 57 w += min(w0 - w, L // 2) 58 elif h0 - h > 0: 59 h += min(h0 - h, L // 2) 60 return w * h - w1 * h1 61 62 63 solve()
