树链剖分学习笔记（补发）
求大佬指错QaQ
个人推荐的题单：树链剖分练习题
个人感觉树链剖分就是把树上的节点按照某种顺序重新编号一次以便于用线段树、树状数组等维护。
这次讲讲轻重链剖分。模板题
一些概念
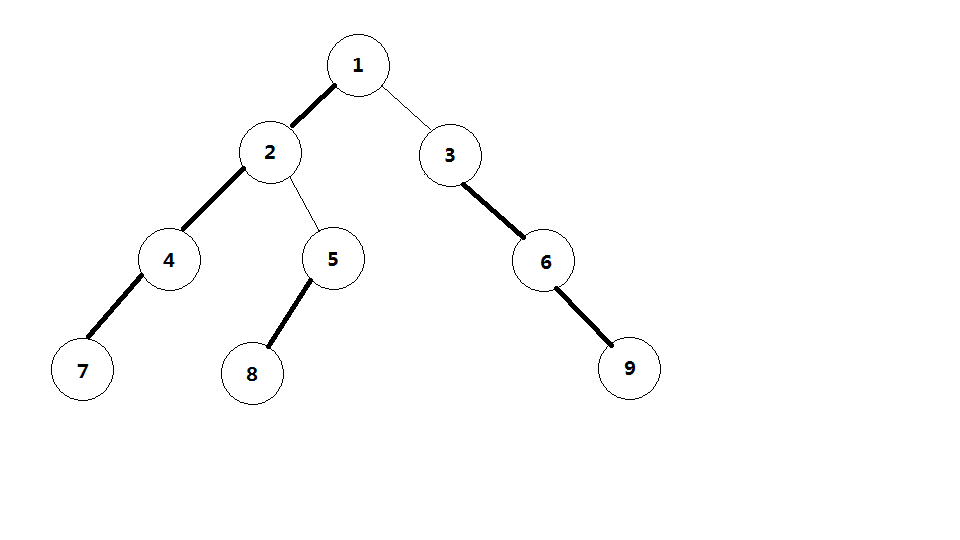
- 重儿子：对于每一个非叶子节点，它的儿子中儿子数量最多的那一个儿子 为该节点的重儿子（图中2的重儿子为4,5的重儿子为8……）
- 轻儿子：对于每一个非叶子节点，它的儿子中 非重儿子 的剩下所有儿子即为轻儿子（图中1的轻儿子为3,3的轻儿子为5）
- 重边：一个节点连接该节点的重儿子的边叫做重边（图中的粗线）
- 轻边：剩下的即为轻边（图中的细线）
- 重链：相邻重边连起来的 连接一条重儿子 的链叫重链
- 对于叶子节点，若其为轻儿子，则有一条以自己为起点的长度为1的重链
- 每一条重链以根或轻儿子为起点
为了用线段树等维护，我们要保证每一个重链上的节点的新编号是连续的，所以新编号（括号内的）可以像下图一样。
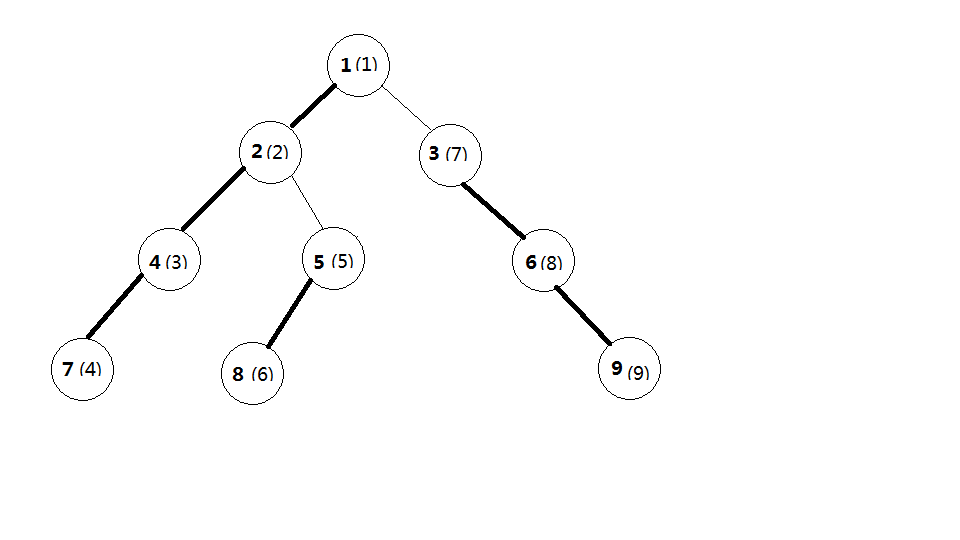
为什么是重点维护重链，而不是别的链
为了提高速度，我们肯定要尽量让多个点在同一条重点维护的链上。
所以我们就把重点维护的链拉向重儿子，最终就是拉成了重链。
实际上也可以是与重儿子的儿子数量差不多的子结点为重链，而且这样更难卡
具体实现
首先要定义如下数组：
son[u]表示节点u的重儿子
siz[u]表示以节点u为子树有多少节点
dep[u]表示节点u的深度
fa[u]表示节点u的父节点
top[u]表示节点u所在重链的顶端节点的原编号
tid[u]表示节点u的新编号
之后就要将这些通过两个dfs求出来。
第一个：
void dfs1(int u) { //递归到的子树的根节点
siz[u]=1;//先算上自己
for(int i=head[u]; i; i=edge[i].next) { //枚举子节点
int v=edge[i].v;
if(v==fa[u])continue;//是父节点就跳过
fa[v]=u;
dep[v]=dep[u]+1;//深度+1
dfs1(v);//递归
if(siz[v]>siz[son[u]])
son[u]=v;//以子树节点数最大的为重儿子
siz[u]+=siz[v];//加上这个子树
}
}
第二个：
void dfs2(int u,int tp) { //u为递归到的子树的根节点，tp表示u所在重链的起点
tid[u]=++tot;
top[u]=tp;
if(son[u])
dfs2(son[u],tp);//先拉出重链，保证重链编号连续
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].v;
if(v^fa[u]&&v^son[u])
dfs2(v,v);//拉以轻儿子为起点的重链
}
}
然后可以发现，不仅重链编号连续，而且同一子树的编号也连续（如图）。
所以以x为根的子树的最右端节点为tid[x]+siz[x]-1，然后我们的3,4操作就可以选择直接用线段树的update和query：
...
else if(op==3) {
x=read(),y=read()%mod;
update(1,tid[x],tid[x]+siz[x]-1,y);
} else if(op==4) {
x=read();
printf("%lld\n",query(1,tid[x],tid[x]+siz[x]-1));
}
对于1,2操作，我们执行以下操作直到两个点在同一条重链（如果在同一条重链可以直接算答案）：
（设所在重链顶端的深度更深的那个点为x点）
- ans加上x点到x所在重链端这一段区间的点权和
- 把x跳到x所在链顶端的那个点的上面一个点
我们模拟一下（以下用w[x]表示节点x的权值）
在图中，我们若想求4到8的路径的权值和，执行就如下：
- 发现8的顶端5比4的顶端1更深。
- ans+=w[8]+w[5]，8跳到顶端5的父节点2
- 发现此时2和4的顶端都为1（即在同一条重链上），于是ans+=w[2]+w[4]，结束计算
更新也是一样的：
void upRange(int u,int v,ll val) {
int f1=top[u],f2=top[v];
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(u,v);
swap(f1,f2);
}
update(1,tid[f1],tid[u],val);
u=fa[f1];
f1=top[u];
}
if(dep[u]>dep[v])swap(u,v);
update(1,tid[u],tid[v],val);
}
ll quRange(int u,int v) {
ll ans=0;
int f1=top[u],f2=top[v];
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(u,v);
swap(f1,f2);
}
ans+=query(1,tid[f1],tid[u]);
if(ans>=mod)ans-=mod;
u=fa[f1];
f1=top[u];
}
if(dep[u]>dep[v])swap(u,v);
ans+=query(1,tid[u],tid[v]);
return ans>=mod?ans-mod:ans;
}
...
if(op==1) {
x=read(),y=read();
upRange(x,y,read()%mod);
} else if(op==2) {
x=read(),y=read();
printf("%lld\n",quRange(x,y));
}
完整代码如下：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
bool f=1;
ll x=0;
int c=getchar();
while(c<=47||c>=58) {
f&=c!=45;
c=getchar();
}
while(c>=48&&c<=57) {
x=(x<<3)+(x<<1)+(c&15);
c=getchar();
}
return f?x:-x;
}
const int MAXN=262144;
struct node {
int l,r;
ll sum,lt;
} tr[MAXN<<2];
int w[MAXN],wt[MAXN],n,m,root,mod;
int son[MAXN],siz[MAXN],top[MAXN],dep[MAXN],fa[MAXN],tid[MAXN];
int tot,ecnt,head[MAXN];
struct Edge {
int u,v,next;
} edge[MAXN];
void addedge(int u,int v) {
++ecnt;
edge[ecnt].v=v;
edge[ecnt].next=head[u];
head[u]=ecnt;
}
void build(int num,int l,int r) {
tr[num].l=l;
tr[num].r=r;
tr[num].lt=0;
if(l==r) {
tr[num].sum=wt[l];
return ;
}
const int mid=l+r>>1,ls=num<<1,rs=ls|1;
build(ls,l,mid),build(rs,mid+1,r);
tr[num].sum=tr[ls].sum+tr[rs].sum;
if(tr[num].sum>=mod)tr[num].sum-=mod;
}
void push_down(int num) {
if(tr[num].lt) {
const int ls=num<<1,rs=ls|1;
tr[ls].lt+=tr[num].lt,tr[rs].lt+=tr[num].lt;
if(tr[ls].lt>=mod)tr[ls].lt-=mod;
if(tr[rs].lt>=mod)tr[rs].lt-=mod;
tr[ls].sum=(tr[ls].sum+(tr[ls].r-tr[ls].l+1)*tr[num].lt)%mod;
tr[rs].sum=(tr[rs].sum+(tr[rs].r-tr[rs].l+1)*tr[num].lt)%mod;
tr[num].lt=0;
}
}
void update(int num,int l,int r,ll val) {
if(tr[num].l>=l&&r>=tr[num].r) {
tr[num].sum=(tr[num].sum+val*(tr[num].r-tr[num].l+1))%mod;
tr[num].lt+=val;
if(tr[num].lt>=mod)tr[num].lt-=mod;
return ;
}
push_down(num);
const int ls=num<<1,rs=ls|1;
if(l<=tr[ls].r)
update(ls,l,r,val);
if(tr[rs].l<=r)
update(rs,l,r,val);
tr[num].sum=tr[ls].sum+tr[rs].sum;
if(tr[num].sum>=mod)tr[num].sum-=mod;
}
ll query(int num,int l,int r) {
if(l<=tr[num].l&&tr[num].r<=r)
return tr[num].sum;
push_down(num);
const int ls=num<<1,rs=ls|1;
ll s=0;
if(l<=tr[ls].r)
s+=query(ls,l,r);
if(tr[rs].l<=r)
s+=query(rs,l,r);
return s%mod;
}
void dfs1(int u) {
siz[u]=1;
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].v;
if(v==fa[u])continue;
fa[v]=u;
dep[v]=dep[u]+1;
dfs1(v);
if(siz[v]>siz[son[u]])
son[u]=v;
siz[u]+=siz[v];
}
}
void dfs2(int u,int tp) {
tid[u]=++tot;
wt[tot]=w[u];
top[u]=tp;
if(son[u])
dfs2(son[u],tp);
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].v;
if(v^fa[u]&&v^son[u])
dfs2(v,v);
}
}
void upRange(int u,int v,ll val) {
int f1=top[u],f2=top[v];
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(u,v);
swap(f1,f2);
}
update(1,tid[f1],tid[u],val);
u=fa[f1];
f1=top[u];
}
if(dep[u]>dep[v])swap(u,v);
update(1,tid[u],tid[v],val);
}
ll quRange(int u,int v) {
ll ans=0;
int f1=top[u],f2=top[v];
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(u,v);
swap(f1,f2);
}
ans+=query(1,tid[f1],tid[u]);
if(ans>=mod)ans-=mod;
u=fa[f1];
f1=top[u];
}
if(dep[u]>dep[v])swap(u,v);
ans+=query(1,tid[u],tid[v]);
return ans>=mod?ans-mod:ans;
}
int main() {
scanf("%d%d%d%d",&n,&m,&root,&mod);
for(int i=1; i<=n; ++i)
w[i]=read()%mod;
for(int i=1,u,v; i<n; ++i) {
u=read(),v=read();
addedge(u,v);
addedge(v,u);
}
dfs1(root);
dfs2(root,root);
build(1,1,n);
for(int op,i=1; i<=m; ++i) {
ll x,y;
op=read();
if(op==1) {
x=read(),y=read();
upRange(x,y,read()%mod);
} else if(op==2) {
x=read(),y=read();
printf("%lld\n",quRange(x,y));
} else if(op==3) {
x=read(),y=read()%mod;
update(1,tid[x],tid[x]+siz[x]-1,y);
} else if(op==4) {
x=read();
printf("%lld\n",query(1,tid[x],tid[x]+siz[x]-1));
}
}
return 0;
}
例题1：P4315 月下“毛景树”
这题是边权，而不是点权，那要怎么办呢？
我们考虑把边权转为点权，而转给父节点的话，会因为一个节点有多个儿子而导致出错，我们就可以转给子节点。
代码上实现就和点权题差不多：
第一处，把点权赋给子节点：
void dfs1(int u) {
siz[u]=1;
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].v;
if(v==fa[u])continue;
dep[v]=dep[u]+1;
fa[v]=u;
w[v]=edge[i].w;//这里哦
dfs1(v);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v])
son[u]=v;
}
}
第二处：查询和更新的时候不能算上LCA（最近公共祖先），因为LCA的点权所代表的边权不在该路径上
int quRange(int u,int v) {
int f1=top[u],f2=top[v],s=INT_MIN;
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(f1,f2);
swap(u,v);
}
s=max(s,query(1,tid[f1],tid[u]));
u=fa[f1],f1=top[u];
}
if(u==v)return s;//多了这一行
if(dep[v]<dep[u])swap(u,v);
return max(s,query(1,tid[son[u]]/*还有这里也改了*/,tid[v]));//把LCA去掉
}
第三处：单条边赋值时要选取子节点
if(c[1]=='h') {
w=edge[x<<1].v,k=edge[(x<<1)-1].v;
if(dep[w]<dep[k])w=k;
update1(1,tid[w],tid[w],y);
}
完整代码：
#include <bits/stdc++.h>
using namespace std;
const int MAXN=131072;
inline int read() {
int x=0;
int c=getchar();
bool f=1;
while(c<=47||c>=58) {
f&=c!=45;
c=getchar();
}
while(c>=48&&c<=57) {
x=(x<<3)+(x<<1)+(c&15);
c=getchar();
}
return f?x:-x;
}
struct Edge {
int v,w,next;
} edge[MAXN<<1];
int head[MAXN],ecnt;
void addedge(int u,int v,int w) {
edge[++ecnt].v=v;
edge[ecnt].w=w;
edge[ecnt].next=head[u];
head[u]=ecnt;
}
struct tree {
bool fg;
int mx,l,r,tg,lt;
} tr[MAXN<<2];
int n,d[MAXN][3],w[MAXN],top[MAXN],son[MAXN],fa[MAXN];
int tid[MAXN],tot,wt[MAXN],pid[MAXN],siz[MAXN],dep[MAXN];
void dfs1(int u) {
siz[u]=1;
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].v;
if(v==fa[u])continue;
dep[v]=dep[u]+1;
fa[v]=u;
w[v]=edge[i].w;
dfs1(v);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v])
son[u]=v;
}
}
void dfs2(int u,int tp) {
++tot;
tid[u]=tot;
pid[tot]=u;
top[u]=tp;
wt[tot]=w[u];
if(!son[u])return;
dfs2(son[u],tp);
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].v;
if(v^fa[u]&&v^son[u])
dfs2(v,v);
}
}
void build(int num,int l,int r) {
tr[num].l=l;
tr[num].r=r;
tr[num].fg=tr[num].lt=tr[num].tg=0;
if(l==r) {
tr[num].mx=wt[l];
return;
}
const int mid=l+r>>1,ls=num<<1,rs=ls|1;
build(ls,l,mid),build(rs,mid+1,r);
tr[num].mx=max(tr[ls].mx,tr[rs].mx);
}
void push_down(int num) {
const int ls=num<<1,rs=ls|1;
if(tr[num].fg) {
tr[ls].mx=tr[ls].tg=tr[rs].mx=tr[rs].tg=tr[num].tg;
tr[ls].fg=tr[rs].fg=1;
tr[ls].lt=tr[rs].lt=0;
tr[num].fg=0;
}
if(tr[num].lt) {
tr[ls].mx+=tr[num].lt,tr[ls].lt+=tr[num].lt;
tr[rs].mx+=tr[num].lt,tr[rs].lt+=tr[num].lt;
tr[num].lt=0;
}
}
void update1(int num,int l,int r,int val) {
if(l<=tr[num].l&&tr[num].r<=r) {
tr[num].fg=1;
tr[num].mx=tr[num].tg=val;
tr[num].lt=0;
return;
}
push_down(num);
const int ls=num<<1,rs=ls|1;
if(l<=tr[ls].r)
update1(ls,l,r,val);
if(tr[rs].l<=r)
update1(rs,l,r,val);
tr[num].mx=max(tr[ls].mx,tr[rs].mx);
}
void update2(int num,int l,int r,int val) {
if(l<=tr[num].l&&tr[num].r<=r) {
tr[num].mx+=val;
tr[num].lt+=val;
return;
}
push_down(num);
const int ls=num<<1,rs=ls|1;
if(l<=tr[ls].r)
update2(ls,l,r,val);
if(tr[rs].l<=r)
update2(rs,l,r,val);
tr[num].mx=max(tr[ls].mx,tr[rs].mx);
}
int query(int num,int l,int r) {
if(l<=tr[num].l&&tr[num].r<=r)
return tr[num].mx;
push_down(num);
const int ls=num<<1,rs=ls|1;
int s=INT_MIN;
if(l<=tr[ls].r)
s=max(s,query(ls,l,r));
if(tr[rs].l<=r)
s=max(s,query(rs,l,r));
return s;
}
void upRange1(int u,int v,int val) {
int f1=top[u],f2=top[v];
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(f1,f2);
swap(u,v);
}
update1(1,tid[f1],tid[u],val);
u=fa[f1];
f1=top[u];
}
if(u==v)return ;
if(dep[v]<dep[u])swap(u,v);
update1(1,tid[son[u]],tid[v],val);
}
void upRange2(int u,int v,int val) {
int f1=top[u],f2=top[v];
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(f1,f2);
swap(u,v);
}
update2(1,tid[f1],tid[u],val);
u=fa[f1];
f1=top[u];
}
if(u==v)return ;
if(dep[v]<dep[u])swap(u,v);
update2(1,tid[son[u]],tid[v],val);
}
int quRange(int u,int v) {
int f1=top[u],f2=top[v],s=INT_MIN;
while(f1^f2) {
if(dep[f1]<dep[f2]) {
swap(f1,f2);
swap(u,v);
}
s=max(s,query(1,tid[f1],tid[u]));
u=fa[f1],f1=top[u];
}
if(u==v)return s;
if(dep[v]<dep[u])swap(u,v);
return max(s,query(1,tid[son[u]],tid[v]));
}
char c[10];
int main() {
n=read();
for(int i=1,u,w,v; i<n; ++i) {
u=read(),v=read(),w=read();
addedge(u,v,w);
addedge(v,u,w);
}
dfs1(1);
dfs2(1,1);
build(1,1,n);
int x,y,w,k;
for(scanf("%s",c); c[0]!='S'; scanf("%s",c)) {
x=read(),y=read();
if(c[1]=='h') {
w=edge[x<<1].v,k=edge[(x<<1)-1].v;
if(dep[w]<dep[k])w=k;
update1(1,tid[w],tid[w],y);
} else if(c[1]=='o')
upRange1(x,y,read());
else if(c[1]=='d')
upRange2(x,y,read());
else if(c[1]=='a')
printf("%d\n",quRange(x,y));
}
return 0;
}
