红黑树(138行)
代码的红黑树部分138行。
本文的图中,红/黑点代表红/黑色节点,蓝点代表无关点(或者子树),绿点代表无所谓颜色的点。
红黑树的性质:
- 是一颗二叉搜索树
- 每个节点是红色或者黑色
- 根和NULL节点是黑色节点
- 红色节点的儿子一定是黑色节点
- 根到每个NULL节点的路径上的黑色节点个数相等(叫做黑高度)
根据这些性质可以推出,树深度小于等于二倍黑高度,是级别
旋转
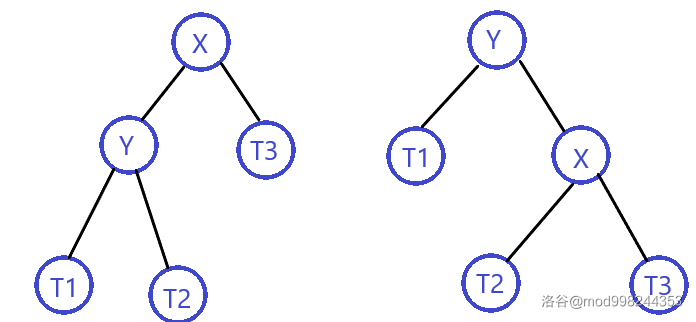
图中从左到右是右旋,从右到左是左旋,不细说了。
inline void rotate(int x) {
static int y,z,k,w;
y=tr[x].fa,z=tr[y].fa,k=tr[y].son[1]==x,w=tr[x].son[k^1];
if(w)tr[w].fa=y;
tr[y].son[k]=w,tr[x].son[k^1]=y,tr[z].son[tr[z].son[1]==y]=x,tr[y].fa=x,tr[x].fa=z;
push_up(y),push_up(x);
}
插入
当原树为空时,直接将根节点赋值为一个新黑色节点即可
其余情况考虑插入一个红色节点,这样就只有可能和性质4发生冲突(即有可能出现双红节点)
之后对这个节点进行双红修正即可。
inline int push(int x) {
if(!rt)return rt=newnode(x,0);
for(int i=rt,id=0; 1; i=tr[i].son[id]) {
++tr[i].siz;
if(tr[i].val==x) //值相同的点合并
return ++tr[i].cnt,i;
id=tr[i].val<x;
if(!tr[i].son[id]) {
tr[i].son[id]=newnode(x,1),tr[tr[i].son[id]].fa=i;
solve_double_red(tr[i].son[id]);
return tr[i].son[id];
}
}
}
双红修正
用一个函数solve_double_red(x)来解决
这个函数的意义是:的子树内已经修正完毕,但有可能是双红,需要接着修正。
首先当为根或的父亲为根时,直接将根节点染为黑色即可。
记得在函数里判断不是双红的情况(直接return)
记函数:时是其父亲的左儿子,时是其父亲的右儿子。
设现在要修正的节点为,其父亲节点为,的节点(的祖父)为,的另一个儿子(的叔父)为
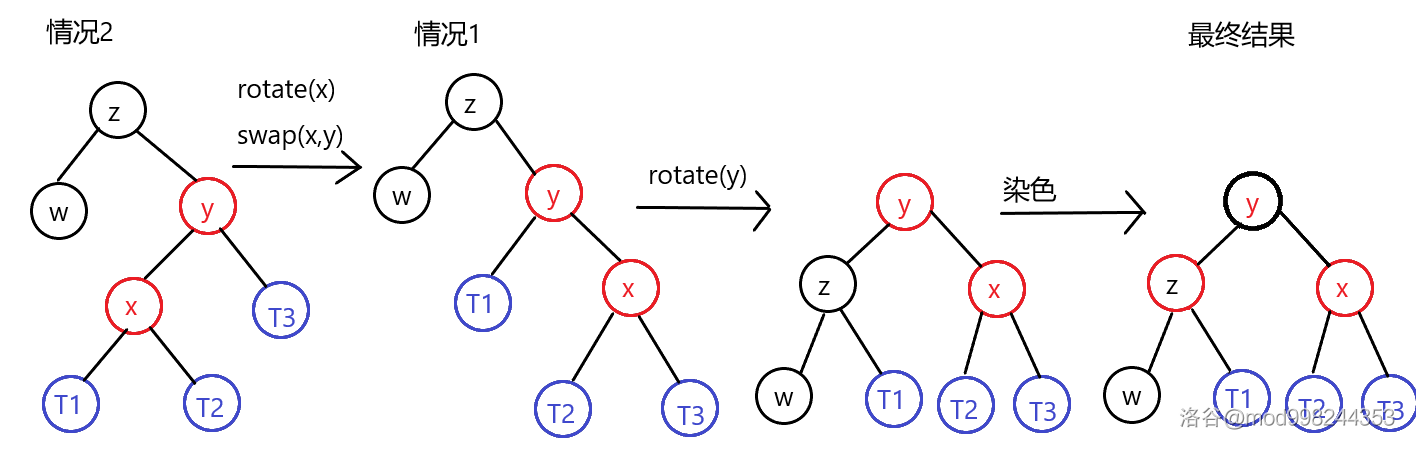
当为黑色节点(或为空)时:(可以发现这两种都是以中间值为根)
-
若,那么
rotate(y)之后把染成黑色,染成红色 -
若,那么
rotate(x),swap(x,y)可以转换为情况
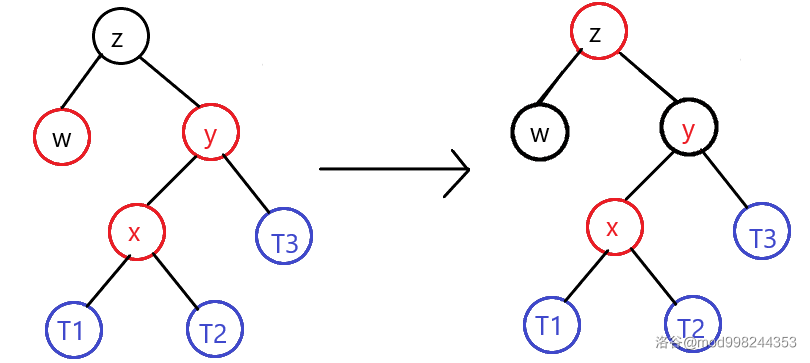
当为红色节点时:将染为黑色,染为红色,递归solve_double_red(z)即可。
void solve_double_red(int x) {
if(x==rt||tr[x].fa==rt) {
tr[rt].col=0;
return;
}
if(!tr[tr[x].fa].col) return;//判断双红
static int y,z,w;
y=tr[x].fa,z=tr[y].fa,w=tr[z].son[tr[z].son[0]==y];
if(!tr[w].col) {//w是黑点
if((tr[y].son[1]==x)^(tr[z].son[1]==y))//id(x)!=id(y)
rotate(x),swap(x,y);
rotate(y),tr[z].col=1,tr[y].col=0;//id(x)=id(y)
return;
}
tr[y].col=tr[w].col=0,tr[z].col=1;
return solve_double_red(z);//尾递归优化
}
删除
首先肯定要找到删除的数对应的节点
如果是唯一的点,直接删除后将根赋值为,其余情况下:
找到当前数的真后继对应的节点,可以交换的数据,转化为删除节点
这样我们删除的节点一定在最后一层。
考虑删除一个在最后一层的节点:
若为红色节点,可以直接删除,不会和任何性质有矛盾
若为黑色节点,删除后会和性质5矛盾,所以删除前要用双黑修正。
inline void pop(int x) {
int i=rt;
for(; tr[i].val^x&&tr[i].son[tr[i].val<x]; i=tr[i].son[tr[i].val<x])
--tr[i].siz;//先找到值x对应的点
--tr[i].siz,--tr[i].cnt;
if(tr[i].cnt) return;
if(i==rt&&!tr[i].son[0]&&!tr[i].son[1])
return rt=0,Q.push(i);//删后是空树
for(x=i; tr[x].son[0]||tr[x].son[1]; ) {//找真后继
static int y;
if(!tr[x].son[0]) y=tr[x].son[1];
else if(!tr[x].son[1]) y=tr[x].son[0];
else for(y=tr[x].son[1]; tr[y].son[0]; y=tr[y].son[0]);
swap(tr[x].val,tr[y].val),swap(tr[x].cnt,tr[y].cnt);
x=y;//可以发现这样删除之后仍满足二叉搜索树的性质
}
Q.push(x);//节点回收
if(!tr[x].col) solve_double_black(x);//删除的节点是黑色,要进行双黑修正
if(tr[x].fa)tr[tr[x].fa].son[tr[tr[x].fa].son[1]==x]=0;
for(i=tr[x].fa; i; i=tr[i].fa) push_up(i);//记得push_up
}
双黑修正
用一个函数solve_double_black(x)来解决
这个函数的意义是:的子树内的黑高度相等,但子树内的黑高度比它兄弟子树内的黑高度小,需要接着修正。
当为根时(整棵树的黑高度都减去),就直接返回。
设为的父亲,为的兄弟。
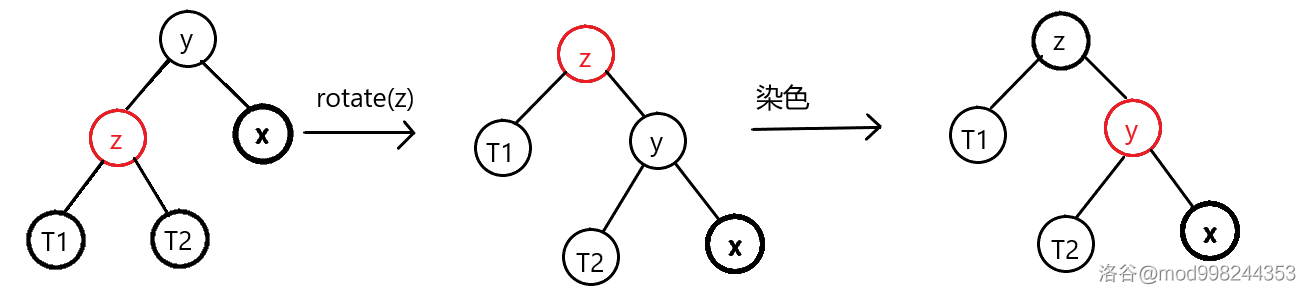
当为红色节点:rotate(z)并交换的颜色,可以转换为为黑的情况。
当为黑色节点且存在红色儿子:(还是中间值做根)
- 若,那么
rotate(z)之后把染成的颜色,染成黑色
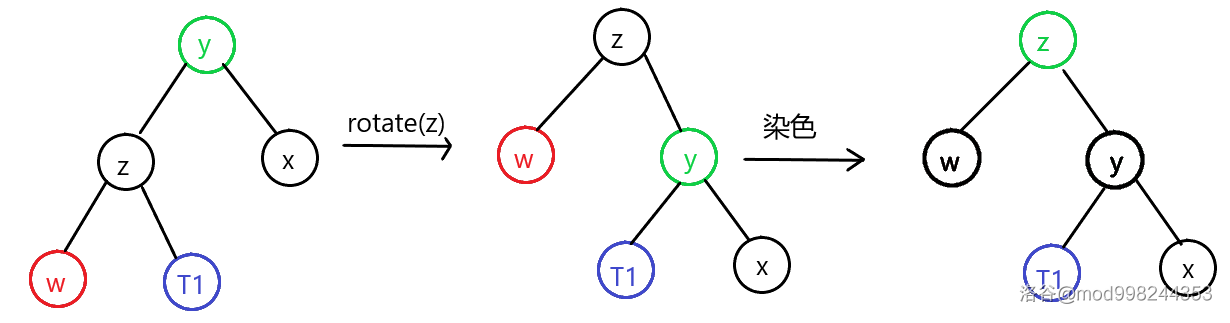
- 若,那么
rotate(w),rotate(w)后把染成的颜色,染成黑色
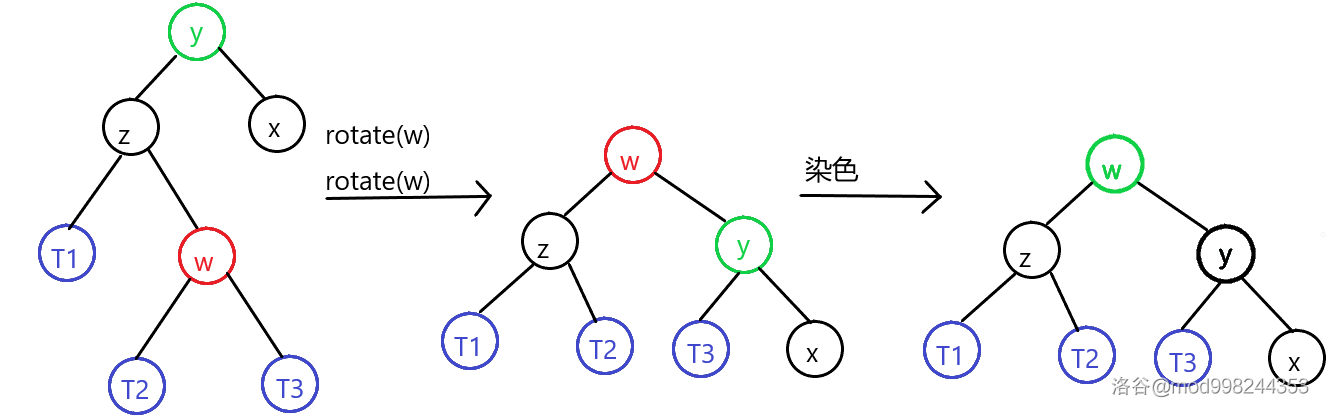
当为黑色节点且无红色儿子:
- 若为红色,染红,染黑就行。
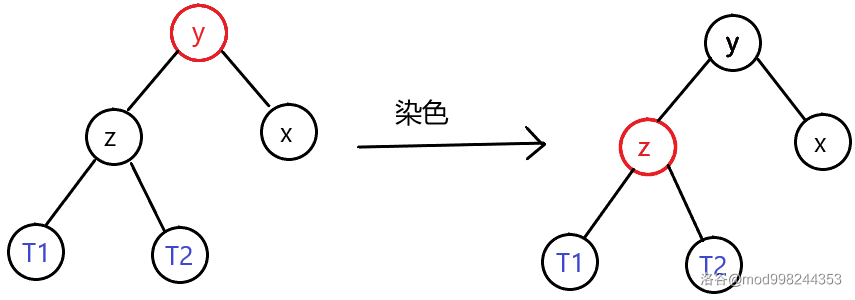
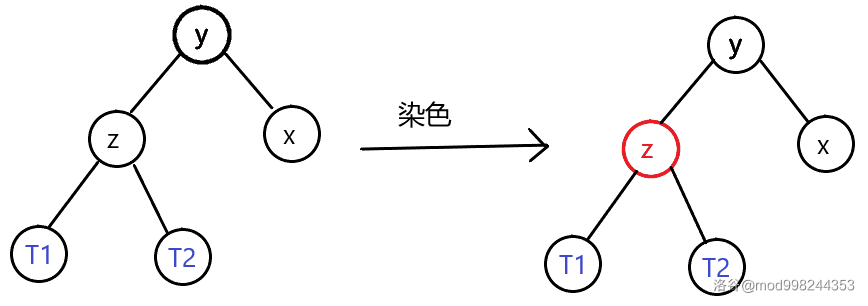
- 若为黑色,染红,递归
solve_double_black(y)
void solve_double_black(int x) {
if(x==rt) {//判根
tr[x].col=0;
return;
}
static int y,z,w,k;
y=tr[x].fa,k=tr[y].son[0]==x,z=tr[y].son[k];
if(tr[z].col) {//z为红点
tr[z].col=0,tr[y].col=1,rotate(z);
y=tr[x].fa,k=tr[y].son[0]==x,z=tr[y].son[k];//旋转后要更新值
}
w=tr[z].son[k];//优先选id相同的红节点
if(tr[w].col) {
tr[z].col=tr[y].col,tr[w].col=tr[y].col=0;
return rotate(z);
}
w=tr[z].son[k^1];
if(tr[w].col) {
tr[w].col=tr[y].col,tr[z].col=tr[y].col=0;
return rotate(w),rotate(w);
}
if(tr[y].col) {
tr[y].col=0,tr[z].col=1;
return;
}
return tr[z].col=1,solve_double_black(y);
}
剩下的部分其实和普通的二叉查找树是一样的,直接放P6136 【模板】普通平衡树(数据加强版)
完整代码吧:(最慢的点512ms)
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1100005;
inline int read() {
static int x,c=getchar(),f;
for(f=1; c<=47||c>=58; c=getchar())f=f&&(c^45);
for(x=0; c>=48&&c<=57; c=getchar())x=(x<<3)+(x<<1)+(c&15);
return f?x:-x;
}
struct node {
int fa,son[2],siz,cnt,val,col;
} tr[MAXN];
queue<int>Q;
int tcnt;
class RBT {
public:
int rt;
inline int newnode(int v,int c) {
static int x;
if(Q.empty()) x=++tcnt;
else x=Q.front(),Q.pop();
tr[x]={0,0,0,1,1,v,c};
return x;
}
inline void push_up(int x) {
tr[x].siz=tr[tr[x].son[0]].siz+tr[tr[x].son[1]].siz+tr[x].cnt;
}
inline void rotate(int x) {
static int y,z,k,w;
y=tr[x].fa,z=tr[y].fa,k=tr[y].son[1]==x,w=tr[x].son[k^1];
if(w)tr[w].fa=y;
if(z)tr[z].son[tr[z].son[1]==y]=x;
else rt=x;
tr[y].son[k]=w,tr[x].son[k^1]=y,tr[y].fa=x,tr[x].fa=z;
push_up(y),push_up(x);
}
void solve_double_red(int x) {
if(x==rt||tr[x].fa==rt) {
tr[rt].col=0;
return;
}
if(!tr[tr[x].fa].col) return;
static int y,z,w;
y=tr[x].fa,z=tr[y].fa,w=tr[z].son[tr[z].son[0]==y];
if(!tr[w].col) {
if((tr[y].son[1]==x)^(tr[z].son[1]==y))
rotate(x),swap(x,y);
rotate(y),tr[z].col=1,tr[y].col=0;
return;
}
tr[y].col=tr[w].col=0,tr[z].col=1;
return solve_double_red(z);
}
inline int push(int x) {
if(!rt)return rt=newnode(x,0);
for(int i=rt,id=0; 1; i=tr[i].son[id]) {
++tr[i].siz;
if(tr[i].val==x)
return ++tr[i].cnt,i;
id=tr[i].val<x;
if(!tr[i].son[id]) {
tr[i].son[id]=newnode(x,1),tr[tr[i].son[id]].fa=i;
solve_double_red(tr[i].son[id]);
return tr[i].son[id];
}
}
}
inline int rnk(int x) {
int res=1,i=rt;
while(i)
if(tr[i].val==x) return res+tr[tr[i].son[0]].siz;
else if(x<tr[i].val)i=tr[i].son[0];
else res+=tr[tr[i].son[0]].siz+tr[i].cnt,i=tr[i].son[1];
return res;
}
inline int kth(int x) {
int res=0,i=rt;
while(1)
if(res+tr[tr[i].son[0]].siz<x&&x<=res+tr[tr[i].son[0]].siz+tr[i].cnt)
return tr[i].val;
else if(x<=res+tr[tr[i].son[0]].siz)
i=tr[i].son[0];
else res+=tr[tr[i].son[0]].siz+tr[i].cnt,i=tr[i].son[1];
}
inline int pre(int x) {
int res=0,i=rt;
while(i)
if(tr[i].val>=x)i=tr[i].son[0];
else res=tr[i].val,i=tr[i].son[1];
return res;
}
inline int suf(int x) {
int res=0,i=rt;
while(i)
if(tr[i].val<=x)i=tr[i].son[1];
else res=tr[i].val,i=tr[i].son[0];
return res;
}
void solve_double_black(int x) {
if(x==rt) {
tr[x].col=0;
return;
}
static int y,z,w,k;
y=tr[x].fa,k=tr[y].son[0]==x,z=tr[y].son[k];
if(tr[z].col) {
tr[z].col=0,tr[y].col=1,rotate(z);
y=tr[x].fa,k=tr[y].son[0]==x,z=tr[y].son[k];
}
w=tr[z].son[k];
if(tr[w].col) {
tr[z].col=tr[y].col,tr[w].col=tr[y].col=0;
return rotate(z);
}
w=tr[z].son[k^1];
if(tr[w].col) {
tr[w].col=tr[y].col,tr[z].col=tr[y].col=0;
return rotate(w),rotate(w);
}
if(tr[y].col) {
tr[y].col=0,tr[z].col=1;
return;
}
return tr[z].col=1,solve_double_black(y);
}
inline void pop(int x) {
int i=rt;
for(; tr[i].val^x&&tr[i].son[tr[i].val<x]; i=tr[i].son[tr[i].val<x])
--tr[i].siz;
--tr[i].siz,--tr[i].cnt;
if(tr[i].cnt) return;
if(i==rt&&!tr[i].son[0]&&!tr[i].son[1])
return rt=0,Q.push(i);
for(x=i; tr[x].son[0]||tr[x].son[1]; ) {
static int y;
if(!tr[x].son[0]) y=tr[x].son[1];
else if(!tr[x].son[1]) y=tr[x].son[0];
else for(y=tr[x].son[1]; tr[y].son[0]; y=tr[y].son[0]);
swap(tr[x].val,tr[y].val),swap(tr[x].cnt,tr[y].cnt);
x=y;
}
Q.push(x);
if(!tr[x].col) solve_double_black(x);
if(tr[x].fa)tr[tr[x].fa].son[tr[tr[x].fa].son[1]==x]=0;
for(i=tr[x].fa; i; i=tr[i].fa) push_up(i);
}
} T;
int n,m,lst,ans;
int main() {
n=read(),m=read();
for(int i=1; i<=n; ++i)T.push(read());
for(int i=1,op,x; i<=m; ++i) {
op=read(),x=read()^lst;
if(op==1)T.push(x);
else if(op==2)T.pop(x);
else if(op==3)lst=T.rnk(x),ans^=lst;
else if(op==4)lst=T.kth(x),ans^=lst;
else if(op==5)lst=T.pre(x),ans^=lst;
else if(op==6)lst=T.suf(x),ans^=lst;
}
printf("%d\n",ans);
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】