数据结构
Basic Data Structure - 数据结构
String - 字符串
// 创建1个或者2个对象,先去常量池判断有没有此变量,有则只在堆上创建一个字符串指向常量池中的字符串;没有则先在常量池中新建字符串,再把引用返回给堆上的对象
String s1 = new String("bill");
// 创建1个或者0个对象,看常量池是否已定义了该变量
String s2 = "billryan";
// beginIndex--起始索引(包括),从0开始;endIndex--结束索引(不包括)
s2.substring(4,8); // return "ryan"
// StringBuilder 非线程安全,单线程下效率高;StringBuffer线程安全,效率低一下
StringBuilder s3 = new StringBuilder(s2.substring(4,8));
s3.append("bill");
String s2New = s3.toString(); // return "ryanbill"
// 将字符串转化为字符数组
char[] s2Char = s2.toCharArray();
// index从0开始算
char ch = s2.charAt(4); // return 'r'
// 寻找字符在字符串中第一次出现的索引
int index = s2.indexOf('r'); // return 4.如果没找到,返回-1
Linked List - 链表
链表是线性表的一种。线性表是最基本、最简单、也是最常用的一种数据结构。线性表中的数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其他数据元素都是首尾相连的。线程表有两种储存结构,一种是顺序存储结构,另一种是链式存储结构。我们常用的数组就是典型的顺序存储结构。
相反,链式存储结构就是两个相邻元素在内存中可能是不相邻的,每个元素都有一个指针域,指针域一般存储着到下一个元素的指针。这种存储方式的优点是定点插入和定点删除的时间复杂度为O(1),而且不会浪费太多内存,添加元素的时候才会申请内存,删除元素会释放内存。缺点是访问的时间复杂度最坏为O(n)。
顺序表的特性是随机读取,即访问一个元素的时间复杂度为O(1),链式表的特性是插入和删除时间复杂度为O(1)。
链式就是链式存储的线性表。根据指针域的不同,链表分为单项链表、双向链表、循环链表等等。
// java类表示
public class ListNode {
public int val;
public ListNode next;
public ListNode(int val) {
this.val = val;
this.next = null;
}
}
链表的基本操作
反向链表
链表的基本形式是:1 -> 2 -> 3 -> null,反转需要变为 3 -> 2 -> 1 -> null。这里要注意:
- 访问某个节点 curt.next 时,要检验 curt 是否为 null。
- 要把反转后的最后一个节点(即反转前的第一个节点)指向 null。
class ListNode {
int val;
ListNode next;
ListNode(int val) {
this.val = val;
}
}
// 迭代法
class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
while (head != null) {
ListNode temp = head.next;
head.next = prev;
prev = head;
head = temp;
}
return prev;
}
}
// 递归法
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode next = head.next;
ListNode newHead = reverseList(next);
next.next = head;
head.next = null;
return newHead;
}
}
双向链表
和单向链表的区别在于:双向链表的反转核心在于next和prev域的交换,还需要注意的是当前节点和上一个节点的递推。
class DListNode {
int val;
DListNode prev, next;
DListNode(int val) {
this.val = val;
this.prev = this.next = null;
}
}
public DListNode reverse(DListNode head) {
DListNode curr = null;
while (head != null) {
curr = head;
head = curr.next; // 移动到 next 域
curr.next = curr.prev; // prev域 赋值给 next 指针
curr.prev = head; // next 域 赋值给 prev 指针
}
return curr;
}
删除链表中的某个节点
- 删除链表中的某个节点一定需要知道这个点的前继节点,所以需要一直有指针指向前继节点。
- 还有一种删除是伪删除,是指复制一个和要删除节点值一样的节点,然后删除,这样就不必知道其真正的前继节点了。
- 然后只需要把
prev - > next = prev -> next -> next即可。但是由于链表表头可能在这个过程中产生变化,导致我们需要一些特别的技巧去处理这种情况。就是下面提到的 Dummy Node。
链表指针的鲁棒性
综合上面讨论的两种基本操作,链表操作时的鲁棒性问题主要包含两个情况:
- 当访问链表中的某个节点 curt.next 时,一定要先判断 curt 是否为 null,否则会报空指针异常
- 全部操作结束后,判断是否有环;若有环,则置其中一端为 null。
Dummy Node
-
Dummy node 是链表问题中的一个重要的技巧,中文翻译叫 “哑节点” 或者 “假人头结点”。
-
Dummy node 是一个虚拟结点,也可以认为是标杆结点。Dummy node 就是在链表表头 head 前加一个结点指向 head,即 dummy -> head。
-
Dummy node 的使用通常针对单链表没用前向指针的问题,保证链表的 head 不会在删除操作中丢失。
-
除此之外,还有一种用法比较少见,就是使用 dummy node 来进行 head 的删除操作,比如 Remove Duplicates From Sorted List II,一般的方法 current = current.next 是无法删除 head 元素的,所以这个时候有一个 dummy node 在 head 的前面。
-
因此,当链表的 head 有可能变化(被修改或者被删除)时,使用 dummy node 可以很好的简化代码,最终返回 dummy.next 即新的链表。
快慢指针
快慢指针也是一个可以用于很多问题的技巧。所谓快慢指针中的快慢指的是指针向前移动的步长,每次移动的步长较大的即为快,步长较小的即为慢,常用的快慢指针一般是在单链表中让快指针每次向前移动2,慢指针则每次向前移动1。快慢两个指针都从链表头开始遍历,于是快指针到达链表末尾的时候,慢指针刚刚到达中间的位置,于是可以得到中间元素的值。快慢指针在链表相关问题中主要有两个应用:
- 一次遍历便能快速找出未知长度单链表的中间结点。设置两个指针
fast、slow都指向单链表的头结点,其中fast的移动速度是slow的2倍,当fast指向末尾结点的时候,slow正好在中间。 - 判断单链表是否有环:利用快慢指针的原理,同样设置两个指针
fast、slow都指向单链表的头结点,其中fast的移动速度是slow的2倍。- 如果
fast==null,说明该单链表以null结尾,不是循环链表 - 如果
fast=slow,则快指针追上慢指针,说明该链表是循环链表。
- 如果
// 寻找链表的中间结点
class Solution {
public ListNode middleNode(ListNode head) {
ListNode slow = head, fast = head;
// 由于fast每次要跳转fast.next.next,为避免空指针异常,fast.next不能为空,同时fast不能为空
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
}
// 判断是否为环形链表
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
return true;
}
}
return false;
}
}
Binary Tree - 二叉树
-
结构:二叉树是每个节点最多有两个子树的树结构,子树有左右之分,二叉树常用于实现二叉查找树和二叉堆。
-
节点数量关系
-
二叉树的第i层至多有2i-1个节点;深度为k的二叉树至多有2k -1个节点;
-
对于任何一颗二叉树T,如果叶子节点为n0 ,度为2的节点数为n2 ,则n0 = n2 + 1。因为度为1的节点对度为0的节点树木不会有影响,而每增加一个度为2的节点总的来说会相应增加一个度为0的节点。
-
性质二的计算方法为:
- 对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。
- 同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2n2。所以,n 用另外一种方式表示为 n=n1+2n2+1。
- 两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
-
-
特殊二叉树定义:
- 一个深度为k,且有2k - 1 个节点称之为满二叉树;
- 深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中序号为1至n的节点对应时,称之为完全二叉树。
public class TreeNode {
public int val;
public TreeNode left, right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
树的遍历
从二叉树的根节点出发,节点的遍历分为三个主要步骤:
- 对当前节点进行操作(称为“访问”节点,或者根节点)
- 遍历左边子节点
- 遍历右边子节点
访问节点顺序的不同就形成了不同的遍历方式。需要注意的是树的遍历通常使用递归的方法进行理解和实现,在访问元素时也需要使用递归的思想去理解。
按照访问根元素(当前元素)的前后顺序,遍历方式可划分为如下几种:
-
深度优先:先访问子节点,再访问父节点,最后访问第二个子节点。根据根节点相对于左右子节点的访问先后顺序又可细分为以下三种方式:
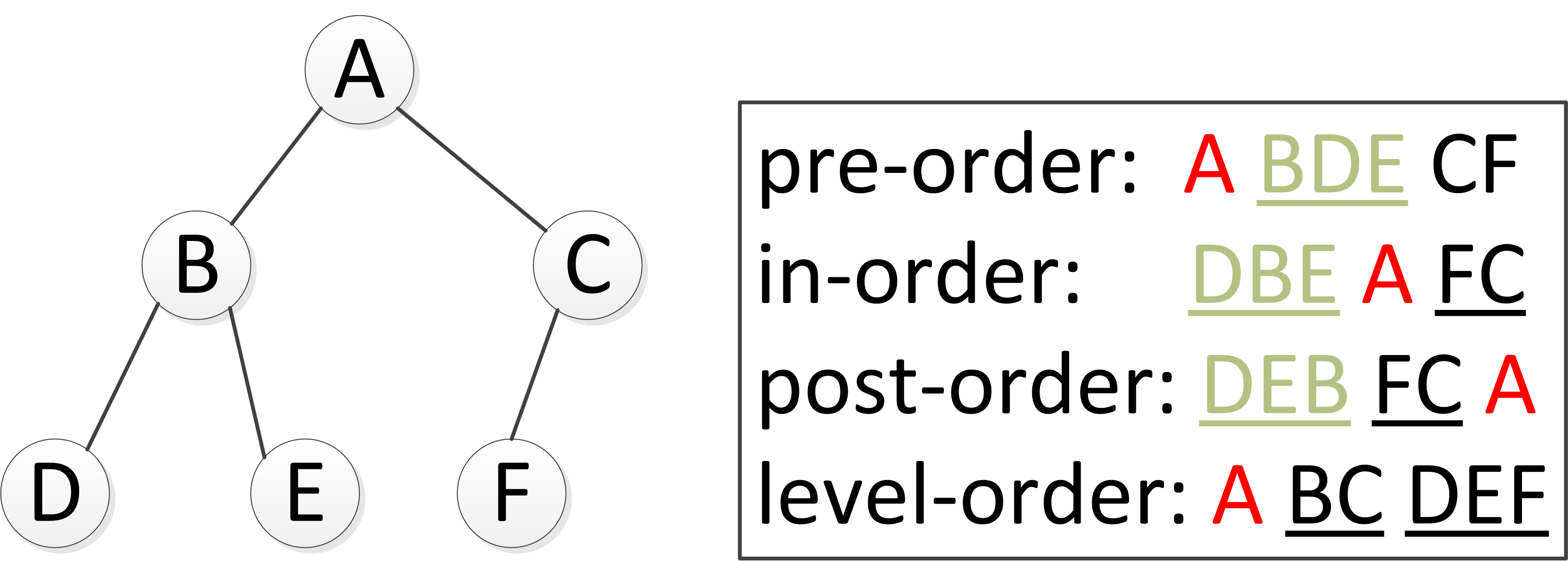
- 前序(pre-order):先根后左再右
- 中序(in-order):先左后根再右
- 后序(post-order):先左后右再根
- 前/中/后序遍历使用递归,也就是栈的思想对二叉树进行遍历。
-
广度优先:先访问根节点,沿着树的宽度遍历子节点,直到所有节点均被访问未知。
- 广度优先一般使用队列的思想对二叉树进行遍历。
如果已知中序遍历和前序遍历或者后序遍历,那么可以完全还原二叉树结构。其中最关键的是前序遍历中第一个节点一定是根,而后序遍历最后一个节点一定是根。中序遍历在得知根节点后又可进一步递归得知左右子树的根节点。但是这种方法也是有适用范围的:元素不能重复!否则无法定位。
// pre-order 递归
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
preOrder(root);
return res;
}
public void preOrder(TreeNode node) {
if (node == null) {
return;
}
res.add(node.val);
preOrder(node.left);
preOrder(node.right);
}
}
// pre-order 迭代
class Solution {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
public List<Integer> preorderTraversal(TreeNode root) {
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
if (node != null) {
res.add(node.val); // 先根
stack.push(node);
node = node.left; // 后左
} else {
node = stack.pop();
node = node.right; // 再右
}
}
return res;
}
}
// in-order 递归
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
inOrder(root);
return res;
}
public void inOrder(TreeNode node) {
if (node == null) {
return;
}
inOrder(node.left);
res.add(node.val);
inOrder(node.right);
}
}
// in-order 迭代
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
if (node != null) {
stack.push(node); // 先左
node = node.left;
} else {
node = stack.pop(); // 后根
res.add(node.val);
node = node.right; // 再右
}
}
return res;
}
}
// post-order 递归
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
postOrder(root);
return res;
}
public void postOrder(TreeNode node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
res.add(node.val);
}
}
// post-order 迭代 (后序:左—>右—>根,转化为特别的中序:根->右—>左,再倒x)
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<Integer> stackData = new Stack<>();
Stack<TreeNode> stackNode = new Stack<>();
TreeNode node = root;
while (!stackNode.isEmpty() || node != null) {
if (node != null) {
stackData.push(node.val);
stackNode.push(node);
node = node.right;
} else {
node = stackNode.pop();
node = node.left;
}
}
while (!stackData.isEmpty()) {
res.add(stackData.pop());
}
return res;
}
}
树类题的复杂度分析
对树相关的题进行复杂度分析时,可统计对每个结点被访问的次数,进而求得总的时间复杂度。
Binary Search Tree - 二叉查找树
- 一颗二叉查找树(BST)是一颗二叉树,其中每个节点都含有一个可进行比较的键及相应的值,且每个节点的键都大于等于左子树中的任意节点的键,而小于右子树中的任意节点的键。
- 使用中序遍历可得到有序数组,这是二叉查找树的又一个重要特征。
- 二叉查找树使用的每个节点含有两个链接,它是将链表插入的灵活性和有序数组查找的高效性结合起来的高效符号表实现。
Queue - 队列
Queue 是一个 FIFO(先进先出)的数据结构,并发中使用较多,可以安全地将对象从一个任务传给另一个任务。
Queue在java中是Interface,其中一种实现是LinkedList, LinkedList 向上转型为 Queue, Queue 通常不能存储 null元素,否则与poll()等方法的返回值混淆。
Queue<Integer> q = new LinkedList<Integer>();
int qLen = q.size(); // get queue length
Queue的方法
| 0:0 | Throws exception | Returns special value |
|---|---|---|
| Insert | add(e) | offer(e) |
| Remove | remove() | poll() |
| Examine | element() | peek() |
优先考虑右侧方法,右侧元素不存在时返回null,判断非空时使用isEmpty()方法,继承自Collection.
Priority Queue - 优先队列
应用程序常常需要处理带有优先级的业务,优先级最高的业务首先得到服务。因此优先队列这种数据结构应运而生。优先队列中的每个元素都有各自的优先级,优先级最高的元素最先得到服务;优先级相同的元素按照其在优先队列中的顺序得到服务。
优先队列可以使用数组或者链表实现,从时间和空间复杂度来说,往往使用二叉堆来实现。
Java中提供PriorityQueue类,该类是 Interface Queue 的另外一种实现,和 LinkedList的区别主要在于排序行为而不是性能,基于 priority heap 实现,非 synchronized,故多线程下应使用 PriorityBlockingQueue.默认为自然序(小根堆),需要其他排序方式可自行实现 Comparator接口,选用合适的构造器初始化。使用迭代器遍历时不保证有序(每次poll()出来之后才是有序),有序访问时需要使用 Arrays.sort(pq.toArray()).
不同方法的时间复杂度:
- enqueuing and dequeuing:
offer,poll,remove()andadd- O(logn) - Object:
remove(Object)andcontains(Object)- O(n) - retrieval:
peek,element, andsize- O(1)
Deque - 双端队列
双端队列(deque,全名double-ended queue)可以让你在任何一端添加或者移除元素,因此它是一种具有队列和栈性质的数据结构。
Java在1.6之后提供了 Deque接口,既可使用ArrayDeque(数组)来实现,也可以使用LinkedList(链表)来实现。前者是一个数组外加首尾索引,后者是双向链表。
Deque<Integer> deque = new ArrayDeque<Integer>();
Methods
| First Element (Head) | Last Element (Tail) | |||
|---|---|---|---|---|
| Throws exception | Special value | Throws exception | Special value | |
| Insert | addFirst(e) |
offerFirst(e) |
addLast(e) |
offerLast(e) |
| Remove | removeFirst() |
pollFirst() |
removeLast() |
pollLast() |
| Examine | getFirst() |
peekFirst() |
getLast() |
peekLast() |
其中offerLast和 Queue 中的offer功能相同,都是从尾部插入。
Heap - 堆
概览
一般情况下,堆通常都指的是二叉堆,二叉堆是一个近似完全二叉树的数据结构,但由于对二叉树平衡及插入/删除操作较为麻烦,二叉堆实际上使用数组来实现。即物理结构为数组,逻辑结构为完全二叉树。子节点的键值或者索引总是小于(或者大于)它的父节点,且每个节点的左右子树又是一个二叉堆(大根堆或者小根堆),常被用作实现优先队列。
特点
- 以数组表示,但以完全二叉树的方式理解
- 唯一能够同时最优地利用空间和时间的方法——最坏情况也能保证 2Nlog2N 次比较和恒定的额外空间
- 在索引从0开始的数组重:
- 父节点
i的左子节点在位置(2*i+1) - 父节点
i的右子节点在位置(2*i+2) - 子节点
i的父节点在位置floor((i-1)/2)
- 父节点
堆的基本操作
以大根堆为例,堆的常用操作如下:
-
最大堆调整:将堆的末端子节点作调整,使得子节点永远小于父节点
-
创建最大堆:将堆所有数据重新排序
-
堆排序:移除位于第一个数据的根节点,并做最大堆调整的递归运算
其中步骤1是给步骤2和3用的

本文来自博客园,作者:LogBiao,转载请注明原文链接:https://www.cnblogs.com/logbiao/p/16418136.html


