02 | 最短路径

最短路径

---

Floyed算法

解决的问题

1. 求解任意两点之间的最短路径
2. 可以处理带有负权边的图， 但不能处理带有“负环”的图

思想

对于要求解的两个点，我们给定任意一个点作为中间点，经过中间点的路径有没有可能比直接到达更短？
动态规划的思想

时间复杂度

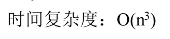
一个小例子

#include <cstdio>
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
int a[101][3];
double f[101][101];
int n, i, j, k, x, y, m, s, e;
int main() {
	freopen("short.in", "r", stdin);    //重定向
	freopen("short.out", "w", stdout);	//重定向
	cin >> n;  //一共有n个点
	for (i = 1; i <= n; ++i) {
		cin >> a[i][1] >> a[i][2];		//记录点的坐标
	}
	cin >> m;							//边的个数
	memset(f, 0x7f, sizeof(f));			//初始化图，double两个字节
	for (i = 1; i <= m; i++) {
		cin >> x >> y;
		f[y][x] = f[x][y] = sqrt(pow(double(a[x][1] - a[y][1]), 2)
			+ pow(double(a[x][2] - a[y][2]), 2));
	}
	cin >> s >> e;
	for (k = 1; k <= n; k++) {                    //加入中间点后的更新
		for (i = 1; i <= n; i++)
			for (j = 1; j <= n; j++)
				if (i != j && i != k && j != k && f[i][k] + f[k][j] < f[i][j])
					f[i][j] = f[i][k] + f[k][j];
	}
	printf("%.2lf\n", f[s][e]);
	return 0;
}
 

输出结果
3.41

dijkstra算法

解决的问题

确定一点到其他任意点的路径最小值

思想

每次仅选一个最小的待确定的点为下一个确定点，并将这个变化更新。
贪心 + DP

一个小例子

#include <cstdio>
#include <cstring>
#define INF 0x3F3F3F3F    //我们建立一个伪最大值，这个是由memset函数特性决定的
using namespace std;
const int M = 1e4 + 10;
const int N = 1000 + 10;
int n, m, s;
int mp[M][N];			//图的临界矩阵
int dis[N];				//dis为距离
bool vis[N];			//vis为待确定点(假设未确定点为蓝点，已确认的为白点)
 
 
void dijkstra(int s)	//求源点s到其他点的最短路径
{
	memset(vis, 0, sizeof(vis));	//0表示蓝点（未确定最短路径的点），1表示白点（确定路径的点）
	memset(dis, INF, sizeof(dis));//默认距离为无穷大
	dis[s] = 0;	//它自身的距离为0
	while (1) {
		int mini = 0, min_ = INF;
		for (int j = 1; j <= n; j++) {
			if (!vis[j] && min_ > dis[j])	//从蓝点中找出最小的值
			{
				mini = j;
				min_ = dis[j];
			}
		}
		//如果没有蓝点，说明结束
		if (mini == 0) break;		//神来之笔，冒泡算法同样用到了
		//如果确定下来一个最小的蓝点
		vis[mini] = 1;
		//那么我们看一看加进来的这个白点对蓝点的影响
		for (int i = 1; i <= n; i++) {
			if (vis[i]==0 && dis[i] > dis[mini] + mp[mini][i])
				dis[i] = dis[mini] + mp[mini][i];
		}
	}
}
 
int main() {
	memset(mp, INF, sizeof(mp)/4);
	while (scanf("%d%d", &n, &m) != EOF && n) {  //注意这里可以一直测试下去
		memset(mp, INF, sizeof(mp));
		for (int i = 0; i < m; i++) {
			int u, v, w;
			scanf("%d%d%d", &u, &v, &w);
			mp[u][v] = mp[v][u] = w;		//图是无权图
		}
		dijkstra(1);						//
		printf("%d\n", dis[n]);				//输出源点1到目标点n的最短路径
	}
	return 0;
}