BZOJ 1492 货币兑换

Description

Input

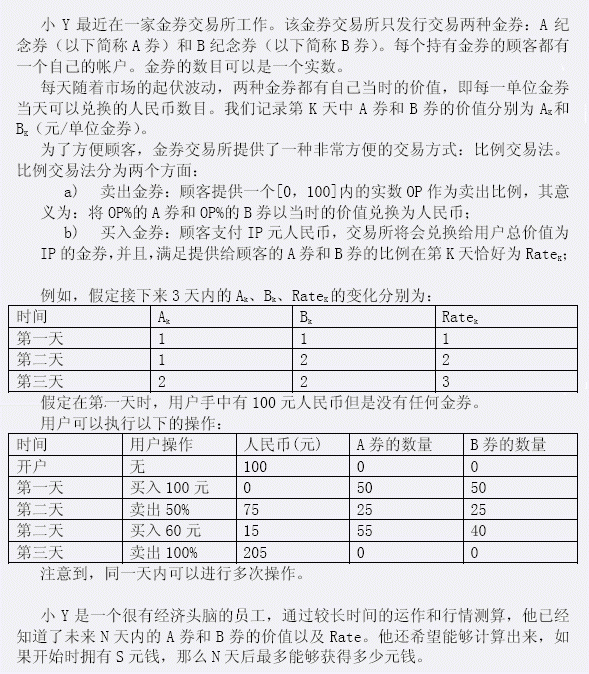
第一行两个正整数\(N,S\)，分别表示小Y 能预知的天数以及初始时拥有的钱数。 接下来\(N\)行，第\(K\)行三个实数\(A_{K},B_{K},Rate_{K}\)，意义如题目中所述。

Output

只有一个实数\(MaxProfit\)，表示第\(N\)天的操作结束时能够获得的最大的金钱数目。答案保留$3￥位小数。

Sample Input

3 100
1 1 1
1 2 2
2 2 3

Sample Output

225.000

HINT

测试数据设计使得精度误差不会超过\(10^{-7}\)。
对于40%的测试数据，满足\(N \le 10\)；
对于60%的测试数据，满足\(N \le 1000\)；
对于100%的测试数据，满足\(N \le 100000\)。

这是一道斜率优化dp的好题。他并不满足单调性，我们只能动态维护凸包。平衡树动态维护凸包并不好码，我们可以用编程复杂度较低的cdq分治。
首先确定一点：最优解一定是贪心地全部买入或卖出所得到的。
\(f_{i}\)表示第\(i\)天所能得到的最多钱数，转移：$$f_{i}=max(f_{i-1},A_{i} \times rate_{j} \frac{f_{j}}{1+rate_{j}}+B_{i} \times \frac{f_{j}}{1+rate_{j}})$$
但是对于这个式子dp是\(O(n^{2})\)的，我们可以令$$X_{i}= rate_{i} \frac{f_{i}}{1+rate_{i}},Y_{i}=\frac{f_{i}}{1+rate_{i}}$$
则dp方程就可以化简为$$f_{i}=max(f_{i-1},A_{j} \times X_{j}+B_{j} \times Y_{j})$$
看出来没，这是一个很明显的斜率优化dp的式子，但是\(X_{i}\)和\(Y_{i}\)都不单调，怎么办。
平衡树动态维护凸包，并不会。于是cdq分治的优势就体现出来了。
cdq分治：对于\(l \thicksim r\)一段，我们可以用已经算出来的\(l \thicksim mid\)一段区更新\(mid+1 \thicksim r\)一段。由于\(l \thicksim mid\)一段\(f\)已经确定，所以我们可以对之进行排序，求凸包之类的，借之更新\(mid+1 \thicksim r\)。
我们只需对于确定\(l \thicksim mid\)一段求凸包，然后用每个\(mid+1 \thicksim r\)里的元素进行二分更新\(f\)即可。时间复杂度\(O(nlog^{2}n)\)。

#include<cmath>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;

#define maxn 100010
int n; double f[maxn],rate[maxn],ak[maxn],bk[maxn];
struct NODE
{
	double x,y;
	friend inline bool operator <(const NODE &a,const NODE &b) { return a.x < b.x; }
	friend inline double operator /(const NODE &a,const NODE &b) { return a.x*b.y-a.y*b.x; }
	friend inline NODE operator -(const NODE &a,const NODE &b) { return (NODE){a.x-b.x,a.y-b.y}; }
	inline double alpha() { return atan2(y,x); }
}ask[maxn],ham[maxn];
double bac[maxn];

inline int find(double key,int l,int r)
{
	int mid;
	while (l <= r)
	{
		mid = (l + r) >> 1;
		if (bac[mid] > key) l = mid+1;
		else r = mid - 1;
	}
	return l;
}

inline void work(int l,int r)
{
	if (l == r)
	{
		f[l] = max(f[l-1],f[l]);
		ask[l].x = f[l]/(ak[l]*rate[l]+bk[l]);
		ask[l].y = ask[l].x*rate[l];
		return;
	}
	int mid = (l + r) >> 1;
	work(l,mid);
	sort(ask+l,ask+mid+1);
	int m = 0;
	for (int i = mid;i >= l;--i)
	{
		while (m > 1&&(ham[m]-ham[m-1])/(ask[i]-ham[m-1]) <= 0) --m;
		ham[++m] = ask[i];
	}
	reverse(ham+1,ham+m+1);
	for (int i = 1;i < m;++i) bac[i] = (ham[i+1]-ham[i]).alpha();
	for (int i = mid+1;i <= r;++i)
	{
		double k = (NODE) {ak[i],-bk[i]}.alpha();
		int pos = find(k,1,m-1);
		f[i] = max(f[i],bk[i]*ham[pos].x+ak[i]*ham[pos].y);		
	}
	work(mid+1,r);
}

int main()
{
	freopen("1492.in","r",stdin);
	freopen("1492.out","w",stdout);
	scanf("%d%lf",&n,&f[0]);
	for (int i = 1;i <= n;++i)
		scanf("%lf %lf %lf",ak+i,bk+i,rate+i);
	work(1,n);
	printf("%.3lf",f[n]);
	fclose(stdin); fclose(stdout);
	return 0;
}