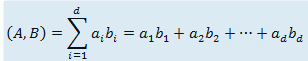BZOJ 3243 向量内积
Description
两个\(d\)维向量\(A=[a_{1},a_{2},...,a_{d}]\)与\(B=[b_{1},b_{2},...,b_{d}]\)的内积为其相对应维度的权值的乘积和,即:
现有\(n\)个\(d\)维向量\(x_{1},...,x_{n}\),小喵喵想知道是否存在两个向量的内积为\(k\)的倍数。请帮助她解决这个问题
Input
第一行包含\(3\)个正整数\(n,d,k\),分别表示向量的个数,维数以及待检测的倍数。
接下来\(n\)行每行有\(d\)个非负整数,其中第\(i\)行的第\(j\)个整数表示向量\(x_{i}\)的第\(j\)维权值\(x_{i,j}\)。
Output
包含两个整数,用空格隔开。
如果存在两个向量\(x_{p},x_{q}\)的内积为\(k\)的整数倍,则输出两个向量的编号\(p\)与\(q\)(要求\(p<q\))。如果存在多组这样的向量组合,输出其中任意一组即可。
若不存在这样的向量组合,则输出两个\(-1\)。
Sample Input
5 2
1 0 1 0 1
1 1 0 1 0
0 1 0 1 1
Sample Output
2 3
HINT
这道题的确挺神的,想了几个小时都只能想得到暴力(\(k=2\)的可以二进制压位)。最后还是无奈的自己翻题解自己研究。
以样例为例(\(K = 2\)时):
首先我们令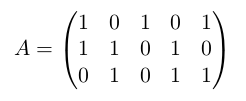
然后我们令\(B\)为\(A\)的转置矩阵(A的行列互换),即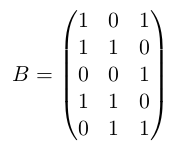
令$$P = A \times B$$
令\(G\)为一个\(n \times n\)的矩阵,里面元素全为\(1\)。
令\(F\)为一个\(n \times n\)的矩阵,除了\(F_{i,i}\)以外的元素全部是\(1\),并且满足\(F_{i,i}+P_{i,i} = 1\)。
我们再令一个$$T=G-F-P$$。
若\(G_{i,j}=1\),则向量\(x_{i}\)与向量\(x_{j}\)的内积为\(0\),\(x_{i}\)与向量\(x_{j}\)为合法解。(注:以上操作均在对\(k\)取模的意义下完成)
但是这样暴力计算矩阵的话无异于暴力。我们可以利用矩阵乘法的性质优化一下。
由于$$T=G-F-P$$
所以我们可以随机一个\(1 \times n\)的矩阵\(X\),就有$$X \times T=X \times (G-F-P)$$
利用乘法分配律拆开$$X \times T = X \times G-X \times F - X \times P = X \times G-X \times F - X \times A \times B$$
由于我们的\(X\)是一个\(1 \times n\)的矩阵,\(X \times A \times B\)可以在\(O(nd)\)的时间内算出来。
矩阵\(F\)的元素我们只需要计算对角线,所以\(F\)我们可以在\(O(nd)\)的时间内算出来。\(X \times F\)可以在\(O(n)\)的时间内计算出来(\(F\)大部分元素为\(0\),只需计算对角线)。
同上,\(X \times G\)也可以线性算,所以算出\(X \times T\)的时间是\(O(nd)\)的。
然后我们令\(Q = X \times T\),若\(Q_{1,i} = 0\)(对\(k\)取模的意义),则\(T\)在第\(i\)行肯定存在元素\(1\),我们只需单独求出此行的结果即可\(O(nd)\)。
这样\(k = 2\)的我们就可以做了。
\(k=3\)的时候有一点小变化。由于在对\(3\)取模的意义下我们除了\(0,1\),还可以得到\(2\)。但是仔细观察我们可以发现$$1{2}=2 \equiv 1(mod ; 3)$$。于是就可以做了。
对于向量\(A,B\)的内积\((A,B)\),我们转而求其平方(\(d=3\)为例)。$$(A,B)^{2}=(a_{1} \times b_{1}+a_{2} \times b_{2}+a_{3} \times b_{3})^{2}$$
将式子拆开我们可以得到
眼熟吧,将\(A,B\)的维度扩展到\(d^{2}\),其实就是
两个新向量的内积。这样就可按照\(k=2\)的做法来做啦!!!
由于常数写大了,不想调试,BZOJ上过不了(时限怎么好像不太对!!!),uoj上被Hack掉了3分。不要在意这些细节。
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
#define maxd (110)
#define maxn (100010)
int N,D,K,DD,ori[maxn][maxd],F[maxn],R[maxn],P[maxn],temp[maxd*maxd];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline int change(int i,int j)
{
if (K&1)
{
int t1 = (j+DD-1)/DD,t2 = j-(t1-1)*DD;
return ori[i][t1]*ori[i][t2];
}
else return ori[i][j];
}
inline bool work()
{
for (int TTT = 10;TTT;--TTT)
{
P[1] = 0;
for (int i = 1;i <= N;++i) { (P[1] += (R[i] = rand()%K)); if (P[1] >= K) P[1] -= K; }
for (int i = 2;i <= N;++i) P[i] = P[i-1];
for (int i = 1;i <= N;++i) { P[i] -= R[i]*F[i]; P[i] %= K; if (P[i] < 0) P[i] += K; }
for (int i = 1;i <= D;++i)
{
temp[i] = 0;
for (int j = 1;j <= N;++j) temp[i] += R[j]*change(j,i);
if (temp[i] >= K) temp[i] %= K;
}
for (int i = 1;i <= N;++i)
{
for (int j = 1;j <= D;++j) P[i] -= temp[j]*change(i,j);
P[i] %= K; if (P[i] < 0) P[i] += K;
}
for (int i = 1;i <= N;++i)
if (P[i])
{
for (int j = 1;j <= N;++j)
{
R[j] = 0;
for (int k = 1;k <= D;++k) (R[j] += change(i,k)*change(j,k));
R[j] %= K;
if (!R[j]&&j != i)
{
if (i < j) printf("%d %d\n",i,j);
else printf("%d %d\n",j,i); break;
}
}
return true;
}
}
return false;
}
int main()
{
freopen("3243.in","r",stdin);
freopen("3243.out","w",stdout);
srand(173); scanf("%d %d %d",&N,&D,&K);
for (int i = 1;i <= N;++i) for (int j = 1;j <= D;++j) ori[i][j] = read()%K;
if (K == 3) DD = D,D *= D;
for (int i = 1;i <= N;++i)
{
for (int j = 1;j <= D;++j) F[i] += change(i,j)*change(i,j);
F[i] %= K; F[i] ^= 1;
}
if (work()) return 0; else printf("-1 -1");
fclose(stdin); fclose(stdout);
return 0;
}
这份是真\(\cdot\)标程
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <ctime>
using namespace std;
const int maxn = 120000;
int n, d, k;
int a[maxn][120], b[120][maxn];
int s[2][maxn], t[maxn], g[maxn];
int read() {
int num = 0; char ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
while (ch >= '0' && ch <= '9') {
num = num * 10 + ch - '0';
ch = getchar();
}
return num % k;
}
void find(int o) {
for (int i = 1; i <= n; i++)
if (i != o) {
int sum = 0;
for (int j = 1; j <= d; j++)
sum += a[o][j] * a[i][j];
if (sum % k == 0) {
printf("%d %d", min(o, i), max(o, i));
return;
}
}
}
void mul(int o) {
if (o == 1) {
if (k == 2) {
memset(t, 0, sizeof(t));
for (int i = 1; i <= d; i++)
for (int j = 1; j <= n; j++)
t[i] = (t[i] + b[i][j] * s[0][j]) & 1;
memset(s[0], 0, sizeof(s[0]));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= d; j++)
s[0][i] = (s[0][i] + a[i][j] * t[j]) & 1;
} else {
memset(t, 0, sizeof(t));
for (int i = 1; i <= d; i++)
for (int j = 1; j <= d; j++)
for (int l = 1; l <= n; l++)
t[i * d + j] = (t[i * d + j] + b[i][l] * b[j][l] * s[0][l]) % 3;
memset(s[0], 0, sizeof(s[0]));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= d; j++)
for (int l = 1; l <= d; l++)
s[0][i] = (s[0][i] + a[i][j] * a[i][l] * t[j * d + l]) % 3;
}
}
else {
int sum = 0;
for (int i = 1; i <= n; i++) sum += s[1][i];
for (int i = 1; i <= n; i++)
s[1][i] = (sum - (1 - g[i]) * s[1][i]) % k;
}
}
void solve() {
srand(241);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= d; j++)
b[j][i] = a[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= d; j++) {
g[i] = (g[i] + a[i][j] * a[i][j]) % k;
if (k == 3) g[i] = (g[i] * g[i]) % 3;
}
for (int t = 1; t <= 10; t++) {
for (int i = 1; i <= n; i++) s[0][i] = rand() & 1;
for (int i = 1; i <= n; i++) s[1][i] = s[0][i];
mul(1); mul(2);
for (int i = 1; i <= n; i++)
if (s[0][i] != s[1][i]) {
find(i);
return;
}
}
printf("-1 -1");
}
int main() {
freopen("3243.in", "r", stdin);
freopen("check.out", "w", stdout);
scanf("%d %d %d", &n, &d, &k);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= d; j++)
a[i][j] = read();
solve();
return 0;
}