分治法求解全排列问题

问题 A: 分治法求解全排列问题

时间限制: 1 Sec  内存限制: 128 MB
提交: 2896  解决: 1431
[状态] [讨论版] [提交] [命题人:外部导入]

题目描述

设R=(1, 2, .., n)，计算R的全排列。 分治法求解全排列的算法思想： 设R=(1, 2, .., n)的全排列为P(R)， 若R=()，则P()=()； 否则，P(R)={(1)P(2, 3, .., n),(2)P(1, 3, .., n), (3)P(2, 1, .., n), .., (n)P(2, .., n-1, 1)}； 同样地，P(2, 3, .., n)={(2){3, 4, .., n}, (3){2, 4, .., n}, .., (n){3, .., n-1, 2}}

输入

输入为一组不大于7的整数。

输出

对每个输入的整数n，用分治法计算并输出1..n的全排列。

样例输入 Copy

1
2
3

样例输出 Copy

1 
1 2 
2 1 
1 2 3 
1 3 2 
2 1 3 
2 3 1 
3 2 1 
3 1 2 


AC代码

#include<iostream>
#include<algorithm>
using namespace std;
int n;
int a[1005];

void per(int n,int m) {
    if (m == n) {
        for (int i = 0; i < n; i++)
            cout << a[i] << " ";
        cout << endl;
        return;
    }
    else {
        for (int i = m; i < n; i++) {//后m个数进行全排列
            swap(a[i], a[m]);
            per(n, m + 1);
            swap(a[i], a[m]);
        }
    }

}

int main()
{ 
    cin >> n;
    for (int i = 0; i < n; i++) {
        a[i] = i + 1;
    }
    per(n, 0);
    
}

假如求n个元素全排列，n的全排列可以分治为n和n-1个元素全排列，n-1的全排列又可以分治为n-1和n-2个元素全排列...

 

 

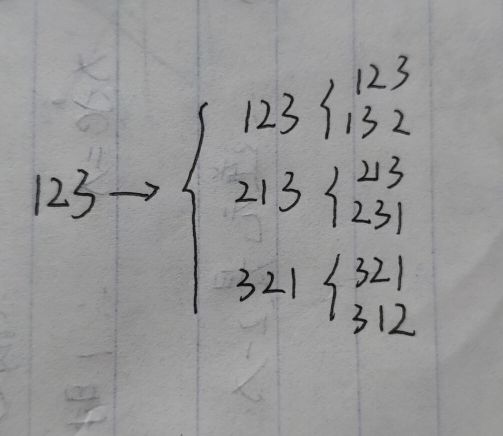
 以123为例，首先在123中1和1交换，然后23中2和2交换，然后3当中，3和3交换，所以第一次排列完后的为123

然后23中2和3交换，然后2当中，2和2交换，第二次就是132...

依此类推...相同颜色的就是相同元素个数的交换