最长公共子序列LCS
LCS:给出两个序列S1和S2,求出的这两个序列的最大公共部分S3就是就是S1和S2的最长公共子序列了。公共部分
必须是以相同的顺序出现,但是不必要是连续的。
LCS具有最优子结构,且满足重叠子问题的性质。所以我们可以用动态规划来解决LCS问题。
由LCS问题的最优子结构可得出递归式:
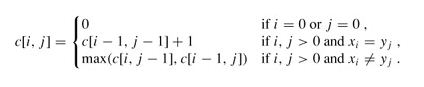
长度的问题我们已经解决了,这次要解决输出最长子序列的问题,
我们采用一个标记函数Flag[i,j],当
①:C[i,j]=C[i-1,j-1]+1 时 标记Flag[i,j]="left_up"; (左上方箭头)
②:C[i-1,j]>=C[i,j-1] 时 标记Flag[i,j]="left"; (左箭头)
③: C[i-1,j]<C[i,j-1] 时 标记Flag[i,j]="up"; (上箭头)
例如:我输入两个序列X=acgbfhk,Y=cegefkh。
1 using System;
2
3 namespace ConsoleApplication2
4 {
5 public class Program
6 {
7 static int[,] martix;
8
9 static string[,] flag;
10
11 static string str1 = "acgbfhk";
12
13 static string str2 = "cegefkh";
14
15 static void Main(string[] args)
16 {
17 martix = new int[str1.Length + 1, str2.Length + 1];
18
19 flag = new string[str1.Length + 1, str2.Length + 1];
20
21 LCS(str1, str2);
22
23 //打印子序列
24 SubSequence(str1.Length, str2.Length);
25
26 Console.Read();
27 }
28
29 static void LCS(string str1, string str2)
30 {
31 //初始化边界,过滤掉0的情况
32 for (int i = 0; i <= str1.Length; i++)
33 martix[i, 0] = 0;
34
35 for (int j = 0; j <= str2.Length; j++)
36 martix[0, j] = 0;
37
38 //填充矩阵
39 for (int i = 1; i <= str1.Length; i++)
40 {
41 for (int j = 1; j <= str2.Length; j++)
42 {
43 //相等的情况
44 if (str1[i - 1] == str2[j - 1])
45 {
46 martix[i, j] = martix[i - 1, j - 1] + 1;
47 flag[i, j] = "left_up";
48 }
49 else
50 {
51 //比较“左边”和“上边“,根据其max来填充
52 if (martix[i - 1, j] >= martix[i, j - 1])
53 {
54 martix[i, j] = martix[i - 1, j];
55 flag[i, j] = "left";
56 }
57 else
58 {
59 martix[i, j] = martix[i, j - 1];
60 flag[i, j] = "up";
61 }
62 }
63 }
64 }
65 }
66
67 static void SubSequence(int i, int j)
68 {
69 if (i == 0 || j == 0)
70 return;
71
72 if (flag[i, j] == "left_up")
73 {
74 Console.WriteLine("{0}: 当前坐标:({1},{2})", str2[j - 1], i - 1, j - 1);
75
76 //左前方
77 SubSequence(i - 1, j - 1);
78 }
79 else
80 {
81 if (flag[i, j] == "

