背包问题:0/1背包问题 普通背包问题(贪心算法只适用于普通背包问题)
//sj和vj分别为第j项物品的体积和价值,W是总体积限制。
//V[i,j]表示从前i项{u1,u2,…,un}中取出来的装入体积为j的背包的物品的最大价值。
第一种:0/1背包问题
最大化 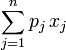 ,受限于
,受限于 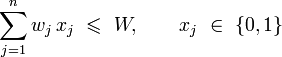
1)若i=0或j=0, V[i,j] = 0
2)若j<si, V[i,j] = V[i-1,j]
3)若i>0且j>=si, V[i,j] = Max{V[i-1,j],V[i-1,j-si]+vi}
第二种:背包问题:在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包。
1)计算yi=vi/si,即该项价值和体积的比
2)按比值的降序来排序
3)从第一项开始装背包,然后是第二项,依次类推,尽可能的多放,直到装满背包。
(贪心算法只适用于普通背包问题,物品可以任意分割,可以得到最优解。如果不能任意分割,贪心法得到的不一定是最优解,而是一个可行解。)
第三种:有界背包问题
最大化 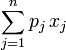 ,受限于
,受限于 
1)若i=0或j=0, V[i,j] = 0
2)若j<si, V[i,j] = V[i-1,j]
3)若i>0且j>=k*si,k={1,2,...,bj}, V[i,j] = Max{V[i-1,j],V[i-1,j-si]+vi,V[i-1,j-2*si]+2*vi,...,V[i-1,j-k*si]+k*vi}

