算法 & 数据结构——收纳箱算法？？？

.　　最近工作上有一个需求，需要将图片打包成图集，以便于让资源更紧凑，利用率更高，提升性能，游戏行内的同志应该很熟练这个操作．通常我们需要用一个app来完成这项工作，最出名的莫过于Texture Packer。

Texture Packer官方示意图

.　　最早接触到这一概念的时候，我还是一个学生，当时玩的《暗黑魔破坏神2》，它有一个背包系统，这个背包系统跟现在大多数游戏都不一样，它的道具存放并非等大小，比如长剑比匕首长，斧头比长剑宽，因此在摆放道具时，不能乱放，不然背包就不够用。

暗黑破坏神2背包截图

.　　这是一个很有意思的设计，但现在基本上绝迹了，以至于我想到游戏中的背包就会不禁想起暗黑破坏神2的背包系统，我在《天龙八部》游戏中，第一次发现了背包自动整理这一项功能，但是它的背包道具都是等大小的，所以平平无奇，但却不由让我想到《暗黑破坏神2》的背包自动整理，它必然会涉及到一个最优排列组合算法。这个疑惑一直困扰了我很多年，它到底是怎么实现的？直到上周，我重新打开了《暗黑破坏神2》这款游戏，发现它根本没有这个功能，童年幻想破灭～

.　　虽然童年幻想破灭了，但成年梦想得跟上，正好工作有这么一个让我去实现的机会，于是我尝试去思考算法，起初想到经典的《背包算法》，仔细研究后发现不太适用，于是放弃。不得不说，厕所是一个很适合思考的地方，因为后来的实现方案是我在蹲厕所的时候突然就想出来了。有没有科学上的解释？

收纳箱算法？

.　　这个算法跟我们日常使用收纳箱的思路很相似，起初收纳箱是空的，它只有一个存放空间，但是很大．之后我们逐个物品往里面放，每次放进去一个物品，原来的空间都会被拆分成两个，最后空间越来越小，直到不能装下剩下的物品，或者物品放完了，这一过程就结束了．

收纳箱示意图

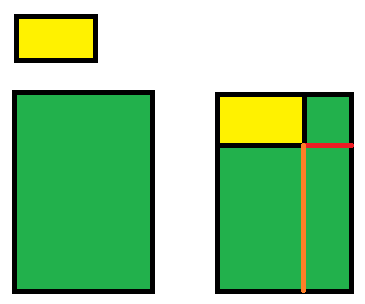
.　　上图清晰描述了收纳箱的存放过程，绿色是收纳箱，黄色是物品，起初收纳箱是空的，只有一个空间，放进物品后，空间被拆分了，这一步是关键，因为放进一个物品会有两种拆分策略，红色线和棕色线分表分表显示了两种拆分策略，如果按红色线拆分，则会产生一个很小的空间和一个很大的空间，如果按棕色线拆分，则产生两个大小均匀的空间。这两种策略对应不同的物品有奇效。每次放进去一个物品，收纳箱的一处空间就会被占用，而算法只考虑没有被占用的空间即可。

.　　接下来就是逐个物品往收纳箱里放，这一步也是关键，因为每次放进一个物品，空间都会被划分，这个划分依据是物品的大小，如果先放进去一个很小的物品，比如1x1大小的物品，那么空间无论怎么分，都会产生一个很狭窄的空间，这个狭窄的空间很可能存不下后续的任何物品，那么这个空间就浪费了，因此在此之前，先对所有物品进行一个排序，这个排序可以按物品的面积，物品的宽度，物品的高度，物品的最长的边，等等。这些排列策略也会影响最终的排列组合。

改进

空间被浪费

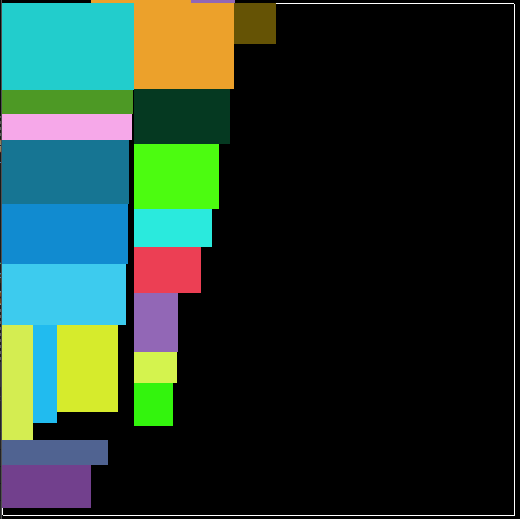
.　　上图是一个空间被浪费的例子，因为上文描述的算法需要已知收纳箱大小，比如已知收纳箱512x512大小，如果物品总面积超出这个大小，则装不下，如果物品远小于这个大小，则浪费空间，所以算法能动态计算大小，那就再好不过了。不过谢天谢地，很容易就可以搞定这个问题，我们只需要提前计算出单个物品最大需要的大小，用这个大小作为收纳箱的大小就可以了。

自动适应

.　　优化过后，已经提高了不少空间利用率，第一个收纳箱装进了最大的物品，后面的收纳箱采用较小的尺寸继续装剩下的物品，直到全部装完为止。但是这里产生了一个新问题，会生成多个收纳箱，如果多个收纳箱都很小，那资源复用率就下降了，所以还需要进一步优化，尽可能提高资源复用率。比如两个128x128可以合并成一个256x256，两个256x256可以合并成一个512x512。

.　　思路是这样的，设定一个打包级别，当这个级别的打包数量达到一个值，就将这个级别提升一级，再重新打包，直到所有级别的收纳箱都没有超出限制。比如，128x128 2，256x256 2，512x512 3 分别代表三个不同的级别，他们是递增关系，当128x128的收纳箱达到2个的时候，说明它需要提升一个级别重新打包，于是级别提升到256x256，依次类推。

最终版本

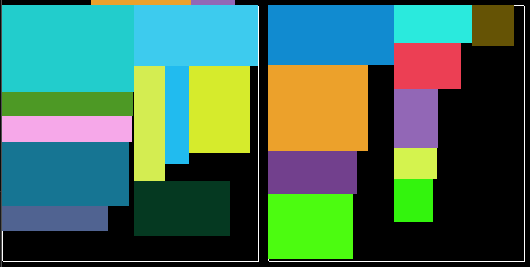
以上结果是采用按棕色线拆分空间，按物品最长边排序，及以下打包级别：

{ 128, 128, 1 },
{ 256, 256, 2 },
{ 512, 512, 3 },
{ 1024, 1024, 4 },
{ 2048, 2048, 100 },

动态图

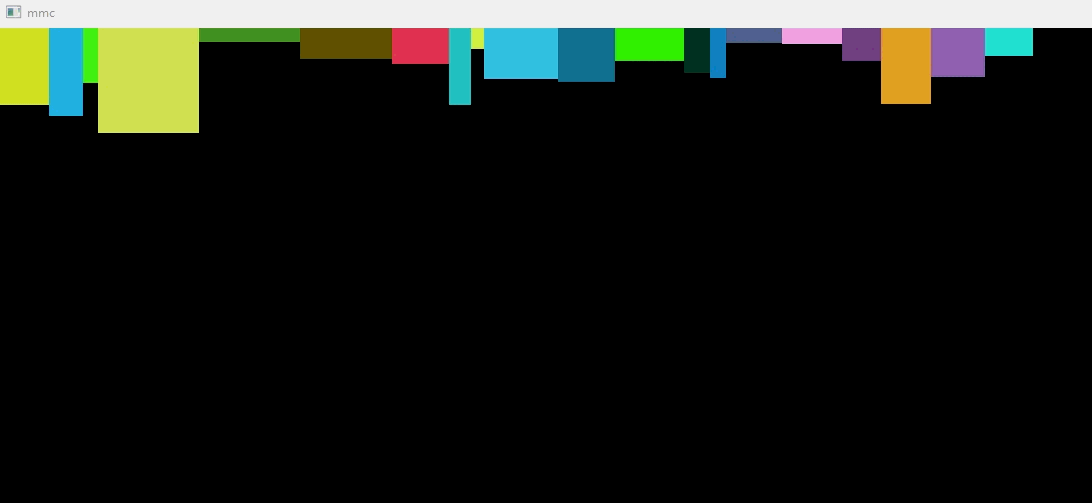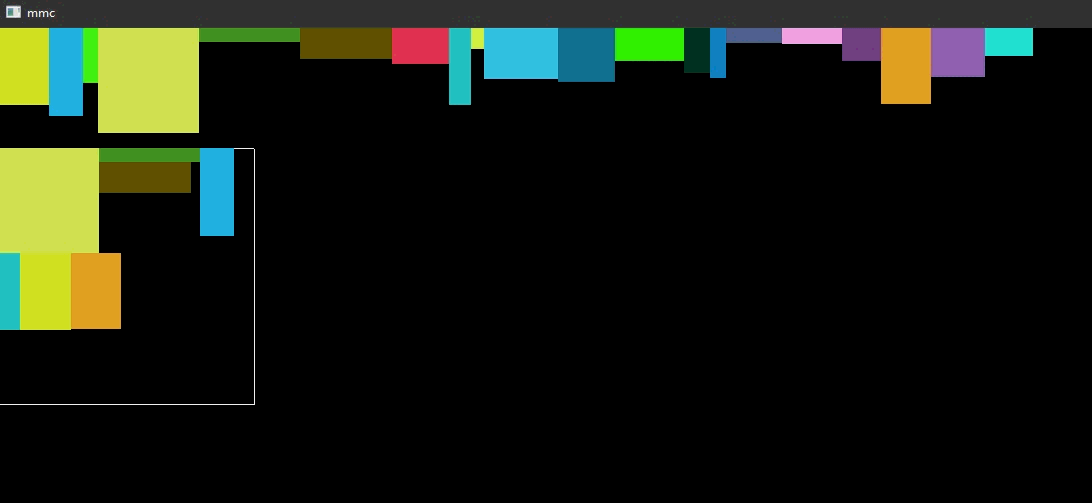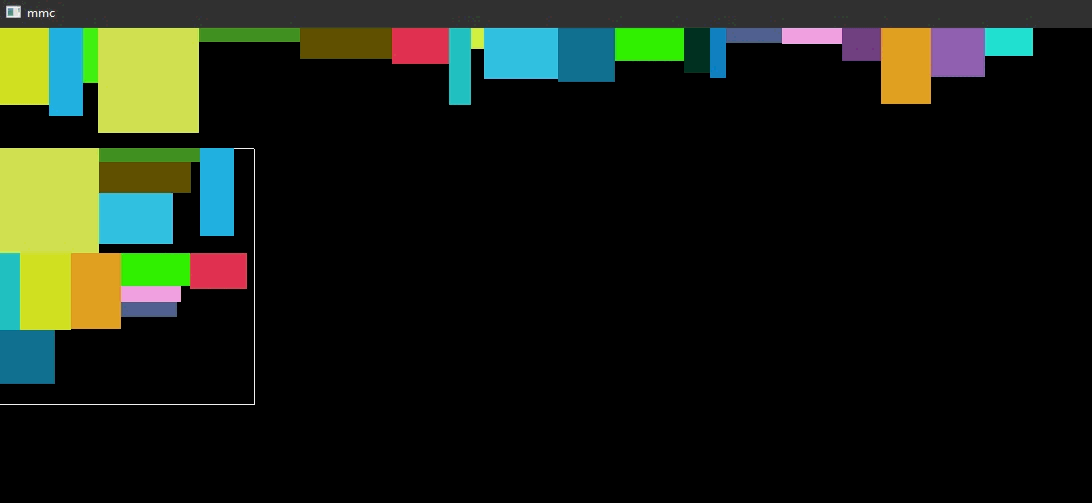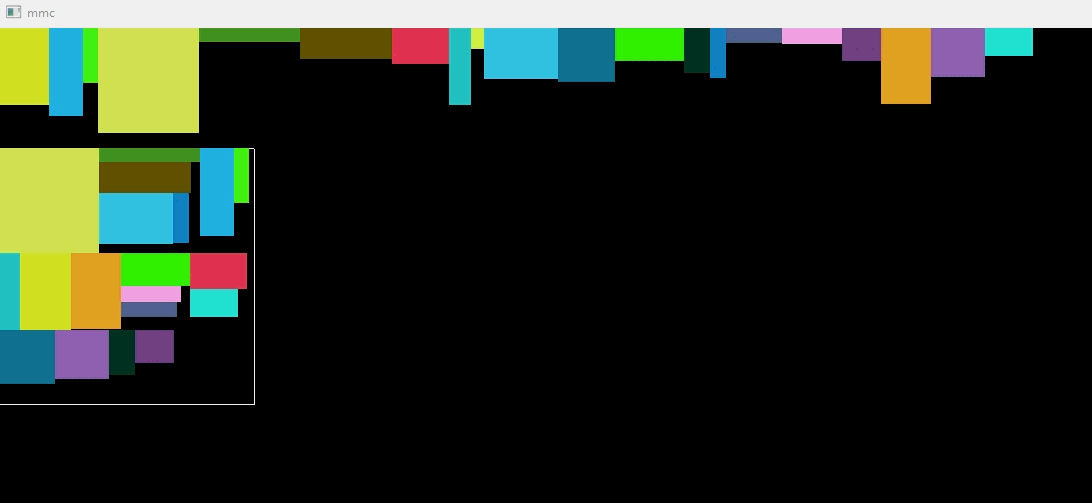
//  storage_box.h
#pragma once

#include <list>
#include <tuple>
#include <array>
#include <vector>
#include <cassert>
#include <algorithm>

using iint = int;
using uint = unsigned int;

class StorageBox {
public:
    struct Item {
        uint i;
        uint w;
        uint h;

        uint GetV() const
        {
            return std::max(w, h);
        }
    };

    struct ResultItem {
        uint i;
        uint x;
        uint y;
        uint w;
        uint h;

        ResultItem(): i((uint)~0)
        { }

        uint GetV() const
        {
            return w * h;
        }

        bool IsReady() const
        {
            return i != (uint)~0;
        }
      
        bool IsContains(const Item & item) const
        {
            return w >= item.w && h >= item.h;
        }

        bool AddItem(const Item & item, ResultItem * out0, ResultItem * out1)
        {
            if (!IsContains(item))
            {
                return false;
            }
            auto nx = x + item.w;
            auto ny = y + item.h;
            auto s0 = (w - item.w) * item.h;
            auto s1 = (h - item.h) * w;
            auto s2 = (w - item.w) * h;
            auto s3 = (h - item.h) * item.w;
            //  两种切分策略:
            //      按最大面积切分
            //      按均匀面积切分
            //if (std::max(s0, s1) > std::max(s2, s3))
            if (std::max(s0, s1) - std::min(s0, s1) < std::max(s2, s3) - std::min(s2, s3))
            {
                out0->x = nx;
                out0->y = y;
                out0->w = w - item.w;
                out0->h = item.h;

                out1->x = x;
                out1->y = ny;
                out1->w = w;
                out1->h = h - item.h;
            }
            else
            {
                out0->x = nx;
                out0->y = y;
                out0->w = w - item.w;
                out0->h = h;

                out1->x = x;
                out1->y = ny;
                out1->w = item.w;
                out1->h = h - item.h;
            }
            w = item.w;
            h = item.h;
            i = item.i;
            return true;
        }
    };

    struct ResultBox {
        uint level;

        std::vector<ResultItem> items;
    };

    //  打包级别
    static constexpr iint PACK_LEVEL[][3] = {
        { 128, 128, 1 },
        { 256, 256, 2 },
        { 512, 512, 3 },
        { 1024, 1024, 4 },
        { 2048, 2048, 100 },
    };

    std::vector<ResultBox> Pack(std::vector<Item> items);

private:
    //  确定使用哪个级别打包图集
    uint CheckLevel(const Item & item);
    uint CheckLevel(const std::vector<Item> & items);
    //  根据图片的V值进行排序
    void SortItems(std::vector<Item> & items);
    void SortItems(std::vector<ResultItem> & items);
    uint CheckLimit(
        std::vector<ResultBox>::iterator cur,
        std::vector<ResultBox>::iterator end);
    //  打包
    ResultBox PackBox(
        std::vector<Item> & items, uint level);
    void PackBox(
        std::vector<Item> & items, uint level, std::vector<ResultBox> & retBoxs);
    //  解包
    void UnpackBox(std::vector<Item> & items, 
        std::vector<ResultBox>::iterator cur,
        std::vector<ResultBox>::iterator end);
};

//  storage_box.cpp
#include "storage_box.h"

std::vector<StorageBox::ResultBox> StorageBox::Pack(std::vector<Item> items)
{
    std::vector<ResultBox> retBoxs;

    PackBox(items, 0, retBoxs);

    for (auto it = retBoxs.begin(); it != retBoxs.end();)
    {
        auto level = it->level;
        auto limit = StorageBox::PACK_LEVEL[level][2];
        auto count = CheckLimit(it, retBoxs.end());
        if (count > limit)
        {
            UnpackBox(items, it, retBoxs.end());
            retBoxs.erase(it, retBoxs.end());
            PackBox(items, level+1, retBoxs);
            it = retBoxs.begin();
        }
        else
        {
            ++it;
        }
    }
    return retBoxs;
}

uint StorageBox::CheckLevel(const Item & item)
{
    for (auto i = 0; i != sizeof(PACK_LEVEL) / sizeof(PACK_LEVEL[0]); ++i)
    {
        if ((uint)PACK_LEVEL[i][0] >= item.w && 
            (uint)PACK_LEVEL[i][1] >= item.h)
        {
            return i;
        }
    }
    return (uint)~0;
}

uint StorageBox::CheckLevel(const std::vector<Item>& items)
{
    uint level = 0;
    for (auto & item : items)
    {
        auto i = CheckLevel(item);
        assert((uint)~0 != i);
        if (i > level) { level = i; }
    }
    return level;
}

void StorageBox::SortItems(std::vector<Item>& items)
{
    std::sort(items.begin(), items.end(), [](const Item & item0, const Item & item1)
        {
            return item0.GetV() > item1.GetV();
        });
}

void StorageBox::SortItems(std::vector<ResultItem> & items)
{
    std::sort(items.begin(), items.end(), [](const ResultItem & item0, const ResultItem & item1)
        {
            return item0.GetV() < item1.GetV();
        });
}

uint StorageBox::CheckLimit(std::vector<ResultBox>::iterator cur, std::vector<ResultBox>::iterator end)
{
    uint count = 0;
    uint level = cur->level;
    cur = std::next(cur);
    while (cur != end && cur->level == level)
    {
        ++cur; ++count;
    }
    return count;
}

StorageBox::ResultBox StorageBox::PackBox(std::vector<Item> & items, uint level)
{
    ResultBox retBox;
    retBox.level = level;

    std::vector<ResultItem> retItems;
    ResultItem retItem;
    retItem.i = (uint)~0;
    retItem.x = 0;
    retItem.y = 0;
    retItem.w = PACK_LEVEL[level][0];
    retItem.h = PACK_LEVEL[level][1];
    retItems.push_back(retItem);

    auto itemIndex = 0u;
    ResultItem retItem0;
    ResultItem retItem1;
    while (itemIndex != items.size())
    {
        auto isNewItem = false;
        for (auto it = retItems.begin(); it != retItems.end(); ++it)
        {
            if (it->AddItem(items.at(itemIndex), &retItem0, &retItem1))
            {
                isNewItem = true;

                //  添加到收纳箱
                retBox.items.push_back(*it);
                retItems.erase(it);

                //  新增2个新收纳箱
                retItems.push_back(retItem0);
                retItems.push_back(retItem1);
                SortItems(retItems);

                //  删除物品
                items.erase(items.begin() + itemIndex);
                break;
            }
        }
        if (!isNewItem) { ++itemIndex; }
    }
    return retBox;
}

void StorageBox::PackBox(std::vector<Item>& items, uint level, std::vector<ResultBox>& retBoxs)
{
    SortItems(items);
    while (!items.empty())
    {
        retBoxs.push_back(PackBox(items, level == 0? CheckLevel(items): level)); 
        level = 0;
    }
}

void StorageBox::UnpackBox(std::vector<Item> & items, std::vector<ResultBox>::iterator cur, std::vector<ResultBox>::iterator end)
{
    for (; cur != end; ++cur)
    {
        for (auto & retItem : cur->items)
        {
            if (retItem.IsReady())
            {
                Item item;
                item.i = retItem.i;
                item.w = retItem.w;
                item.h = retItem.h;
                items.push_back(item);
            }
        }
    }
}

这个算法并不能得到最优排列组合，但是这个算法简单而且在大多数情况下都够用。