人工智能导论期末要点突击

概念总结

明确关系，理解要义，乱杀！@萌狼蓝天

产生式

明确产生式的基本形式，优点、缺点。

了解蕴含式和产生式的区别

产生式的基本形式：P→Q (IF P THEN Q)

• 优点：清晰性、模块性、自然性
• 缺点：难以扩展、规则选择效率较低

蕴含式

蕴含式是产生式的一种特殊情况。

蕴含式：只能表示精确性知识，其逻辑值要么为真，要么为假

产生式：不仅可以表示精确性知识，还可以表示不精确知识。

公式合一判断

要判断两个公式是否为可合一（unifiable），通常使用的方法是基于合一算法（unification algorithm），其中最基本和常用的是Martelli-Montanari合一算法。这里，我将简要描述一种通用的合一算法的基本步骤，以及如何应用它来判断两个公式是否可合一。

关键：每个变量都可以直接映射到一个常量上

合一（Unification）是逻辑和自动定理证明中的一个基本概念，特别是在一阶逻辑和某些编程语言的类型系统中。合一的基本思想是找到一种方式，通过替换变量，使得两个表达式变得相同。

可以合一的情况：

1. 变量和常量：一个表达式中的变量可以被替换为另一个表达式中的常量或更复杂的项，以实现合一。
2. 相同的结构：如果两个表达式具有相同的结构（例如，都是相同的函数符号应用于相同数量的参数），则可以通过合一它们的相应部分来合一整个表达式。
3. 无冲突：如果在合一过程中没有出现任何冲突（例如，试图将同一个变量替换为两个不同的项），则合一通常是可能的。

不可以合一的情况：

1. 结构不匹配：如果两个表达式的结构不同（例如，一个是函数符号，另一个是常量），则通常无法合一。
2. 变量冲突：如果在合一过程中出现冲突，例如试图将同一个变量同时替换为两个不同的项，则合一是不可能的。
3. 循环依赖：如果合一映射引入循环依赖（例如，一个变量被替换为包含自身的项），则通常也无法实现合一。

总之，合一的可能性取决于两个表达式的结构和在合一过程中是否出现冲突。在实际应用中，合一算法通常用于自动推理、程序分析和验证、自然语言处理等领域。

子句集

子句集不可满足判断

如果无法找到一组变量赋值使得子句集中的所有子句同时为真，那么该子句集就是不可满足的。

判断子句集不可满足的一般步骤可以简化为以下过程：

1. 否定目标公式（如果目标是证明某个公式Q为真，则首先否定Q，得到¬Q）。
2. 将否定的公式加入到已知前提的公式集中，形成扩展的公式集。
3. 将这个扩展的公式集转换为子句集的形式。
4. 应用归结原理对子句集中的子句进行归结操作，即反复寻找两个可以归结的子句并推导出它们的归结式。
5. 不断重复归结操作，每次归结得到的归结式都加入到子句集中。如果在这个过程中出现了空子句（即没有任何文字的子句），那么就停止归结。
6. 如果在归结过程中出现了空子句，那么这证明了原目标公式Q为真（因为我们在开始时否定了Q，而现在出现了矛盾），或者说子句集是不可满足的。

这个过程的关键在于应用归结原理和合一算法来推导子句之间的逻辑关系，直到找到一个矛盾（空子句）或者确定没有矛盾为止。在实际应用中，这个过程通常由计算机自动执行，因为对于大规模的子句集，手动执行会非常耗时和低效。

谓词公式化为子句集

利用谓词公式的等价关系：

\[P → Q ⟺ ¬ P ∨ Q \]

\[P ⟷ Q ⟺ ( P ∨ Q ) ∨ ( ¬ P ∨ ¬ Q ) \]

利用谓词公式的等价关系：
双重否定律： ¬ ( ¬ P ) ⟺ P
德摩根律： ¬ ( P ∧ Q ) ⟺ ¬ P ∨ ¬ Q
        ¬ ( P ∨ Q ) ⟺ ¬ P ∧ ¬ Q
量词转换律：¬ ( ∀ x ) P ⟺ ( ∃ x ) ¬ P
          ¬ ( ∃ x ) P ⟺ ( ∀ x ) ¬ P

• 消除蕴含(-->)：A→B 转换为 ¬A∨B
• 分配否定（德摩根定律）¬(P∨Q) 转换为 ¬P∧¬Q

相关符号

谓词公式

存在：∃

任意：∀

且：∧

或：∨

非：¬

示例

10. 设有下列语句，请用相应的谓词公式把它们表示出来。

(1) 有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。

解：
	设：x表示某个人
		Like(x,y) 表示x喜欢y
		meihua：梅花
		juhua：菊花
		有的人喜欢梅花：∃（x）Like(x,meihua)
		有的人喜欢菊花：∃（x）Like(x,juhua))
		有的人既喜欢梅花又喜欢菊花：∃（x）（Like(x,meihua)∧Like(x,Jjuhua))

(2) 重庆市的夏天既炎热又干燥。

解：
	设：x表示某个城市
	Summer(x):表示某个城市的夏天
	Hot(x) 表示x炎热
	Dry(x) 表示x干燥
	重庆：chongqing
	Hot(Summer(chongqing))∧Dry(Summer(chongqing))

(3) 有一个人是所有学生的老师。

解：
	设：x表示某个人
	Student(x) 表示x是学生
	Teach(x,y) 表示：x是y的老师
	∃x(∀y(Student(y))--> Teach(x,y))

语义网络

语义网络是一种图形化的知识表示方法

• 用节点来表示概念、实体或事件
• 用边来表示这些节点之间的关系

在构建语义网络时，我们首先要识别出语句中的关键信息，然后将这些信息用节点和边连接起来。

常用关联词

教科书P40

• 属性关系

  • Have：某个节点具有另外一个节点所描述的属性

  • Can：某个节点能做另一个节点的事情

• 类属关系

  • AKO（A-Kind-of）：某个节点 是 另外一个节点 的一种
  • AMO（A-Member-of）：某个节点 是 另外一个节点的成员
  • ISA（Is-A）：某个节点 是 另外一个节点的实例

• 包含关系

  • part-of：表示某个节点是另外一个节点的一部分

    Part-of和Member-of异同（类属关系和包含关系的异同）

    Part-of、Member-of：都是一部分。表示某个节点是另外一个节点的一部分

    Part-of：不具备属性的继承性。例如 轮胎是汽车的一部分

• 位置关系

  • located-on：某物在另外一个物体之上
  • located-at：某物在某个位置
  • located-under：某物在另外一个物体之下
  • located-inside：某物在另外一个物体之中
  • located-outside：某物在另外一个物体之外

• 相近关系

  • Similar-to：某事物与另外一个事物相似
  • Near-to：表示某事物与另外一个事物接近

• 因果关系

  • if-then：如果……那么……

• 组成关系

  • composed-of：组成关系（一对多的关系，不具备属性继承性）

示例

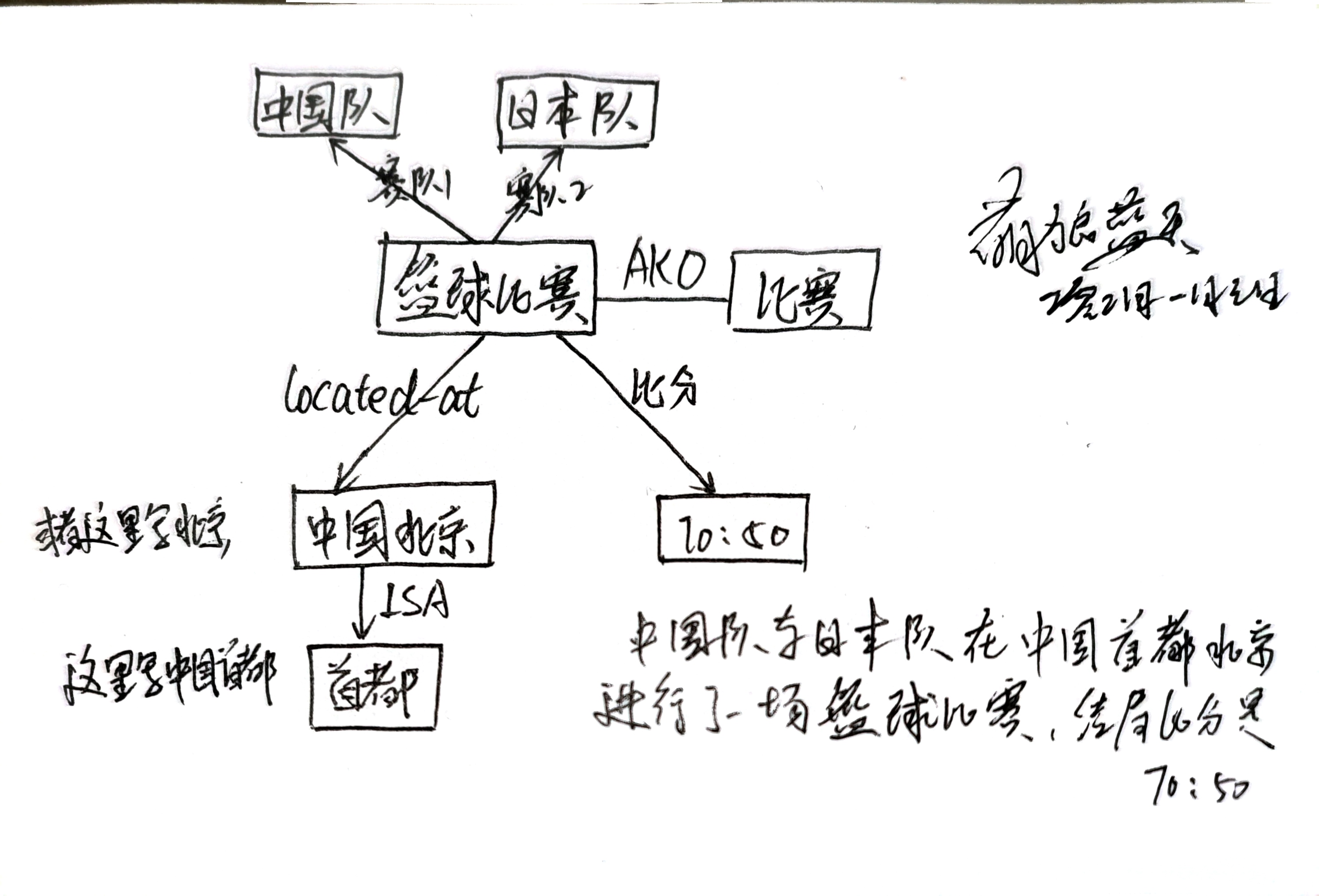
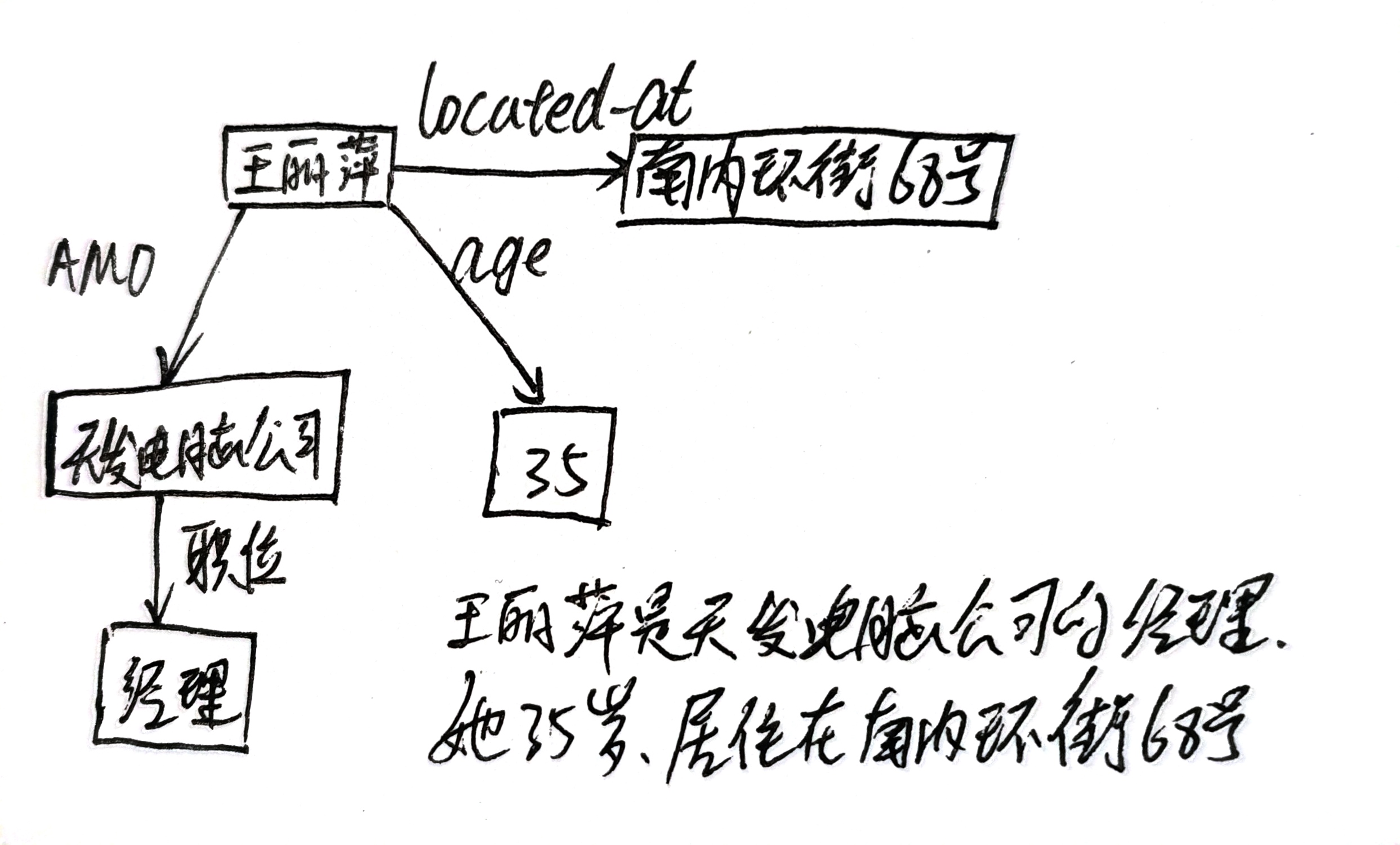
框架

框架的基本结构：

<框架名>
槽名n :侧面名n1  值n1
       侧面名n2  值n2
……
约束:约束条件n

示例：

天气预报：  
    地区：合川  
    日期：今天  
    时间：白天  
    天气状况：阴天  
    风向：东南风  
    风力等级：4级  
    最高气温：11℃  
    最低气温：4℃  
    降水概率：30%