高数笔记(极限与连续)
等价无穷小

两个重要极限
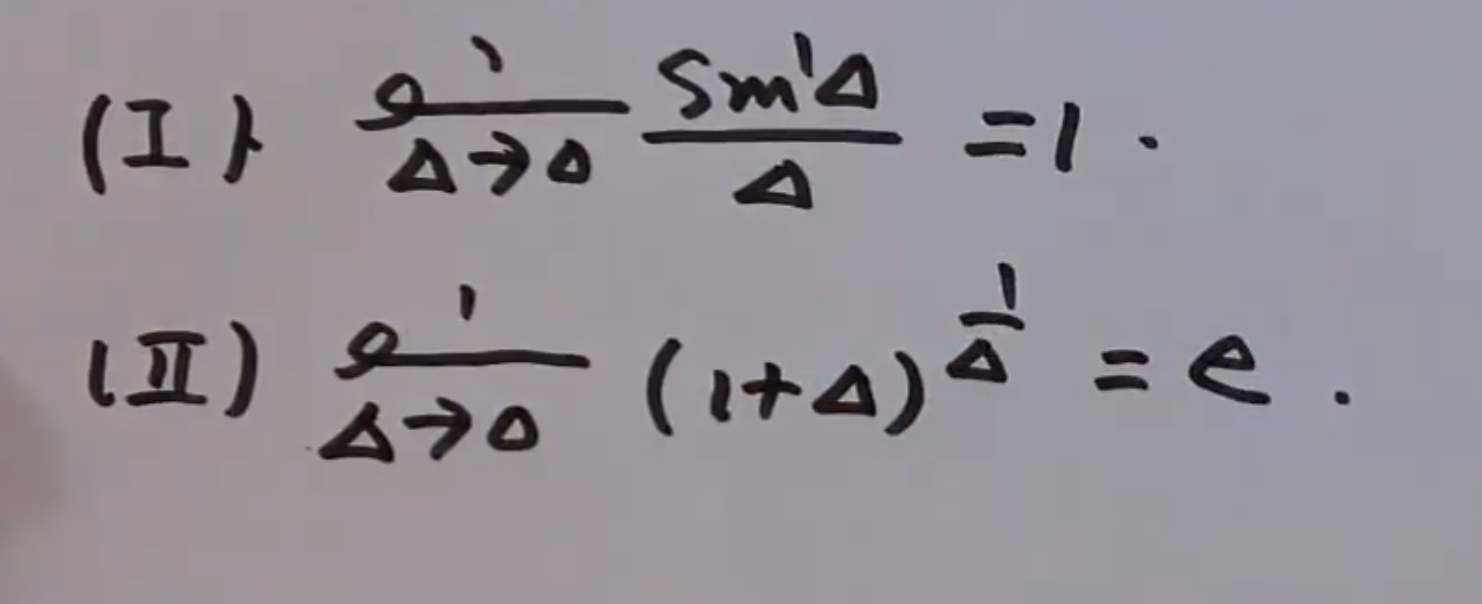
notes

型一
求极限题型
1)先求和

2)夹逼定理

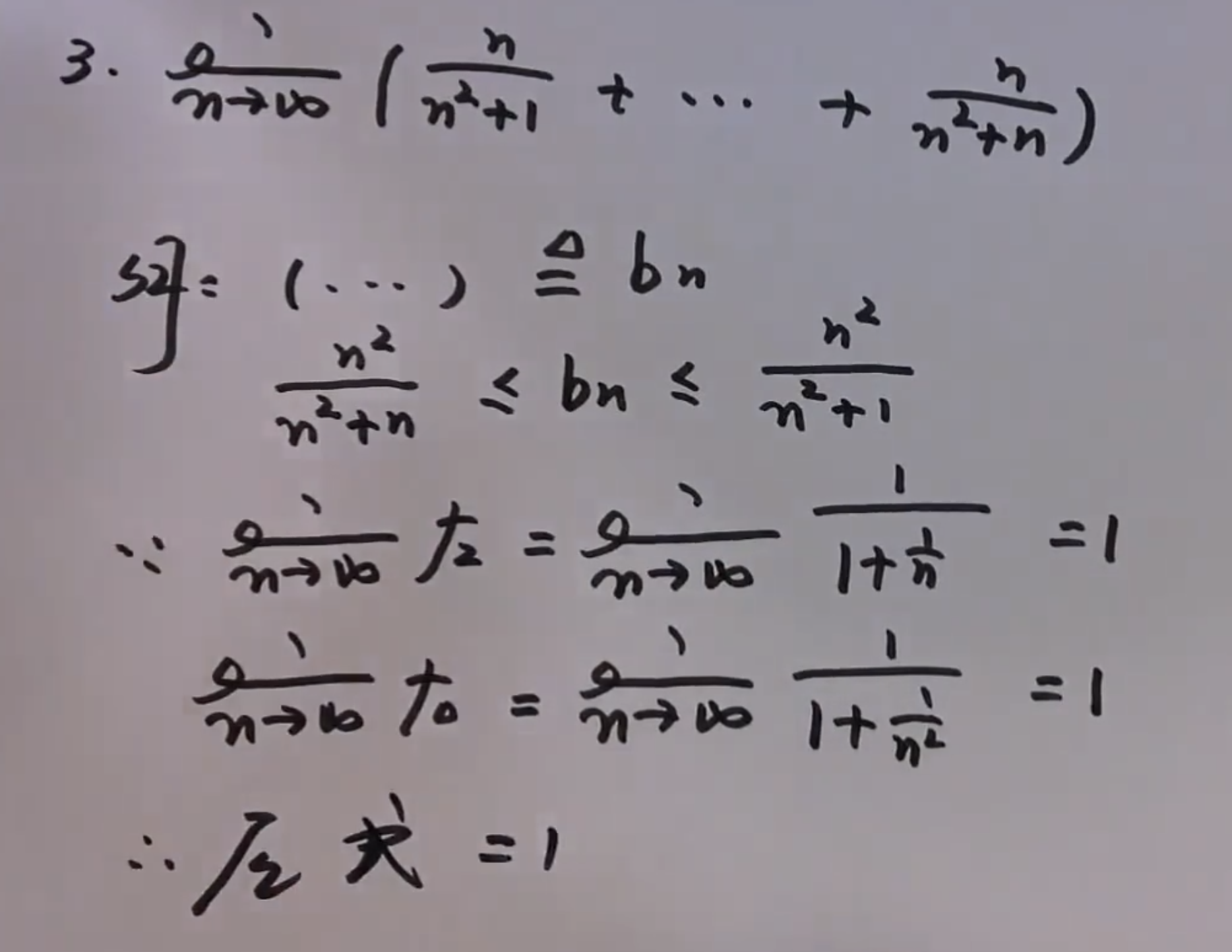
3)(重点)
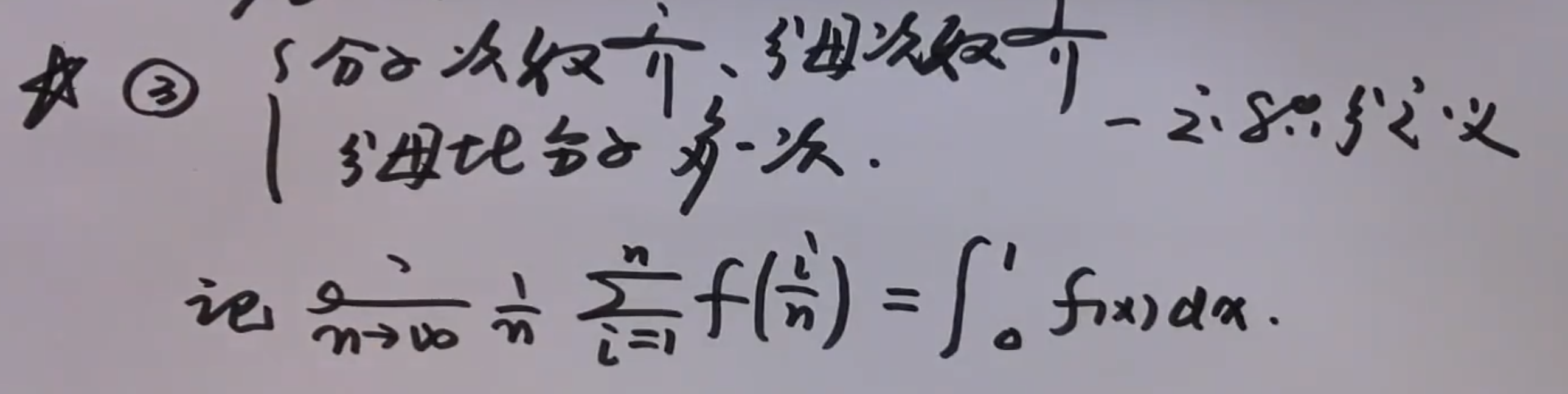
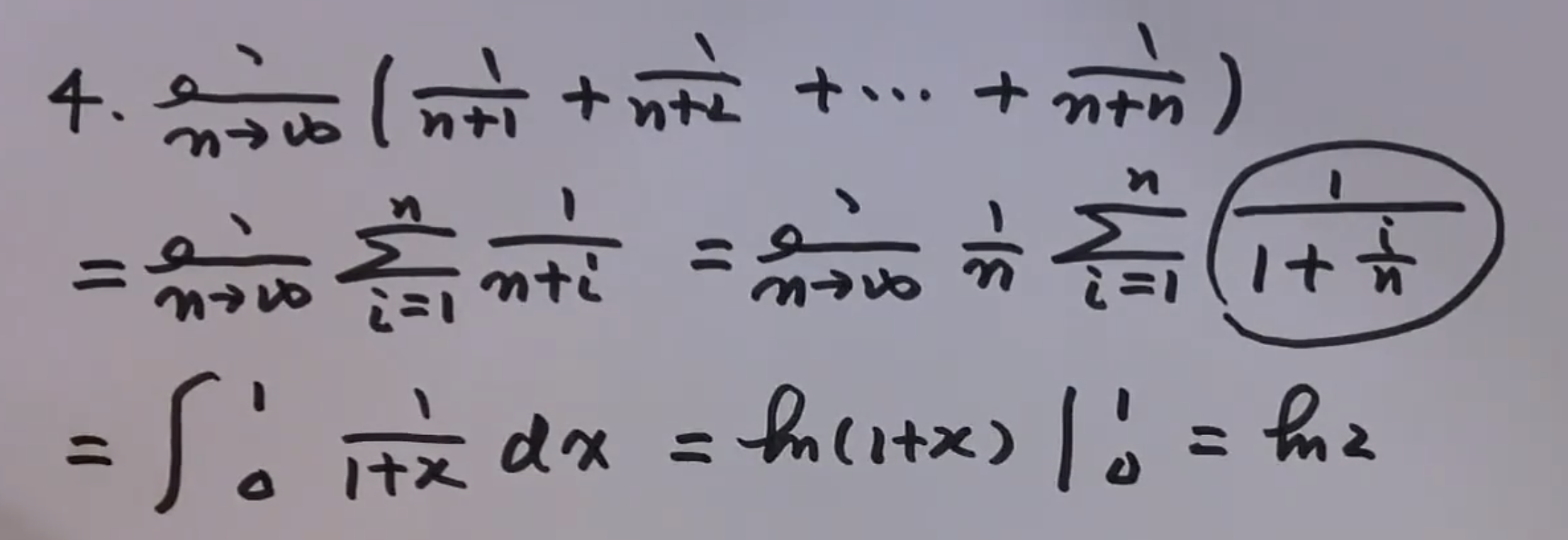
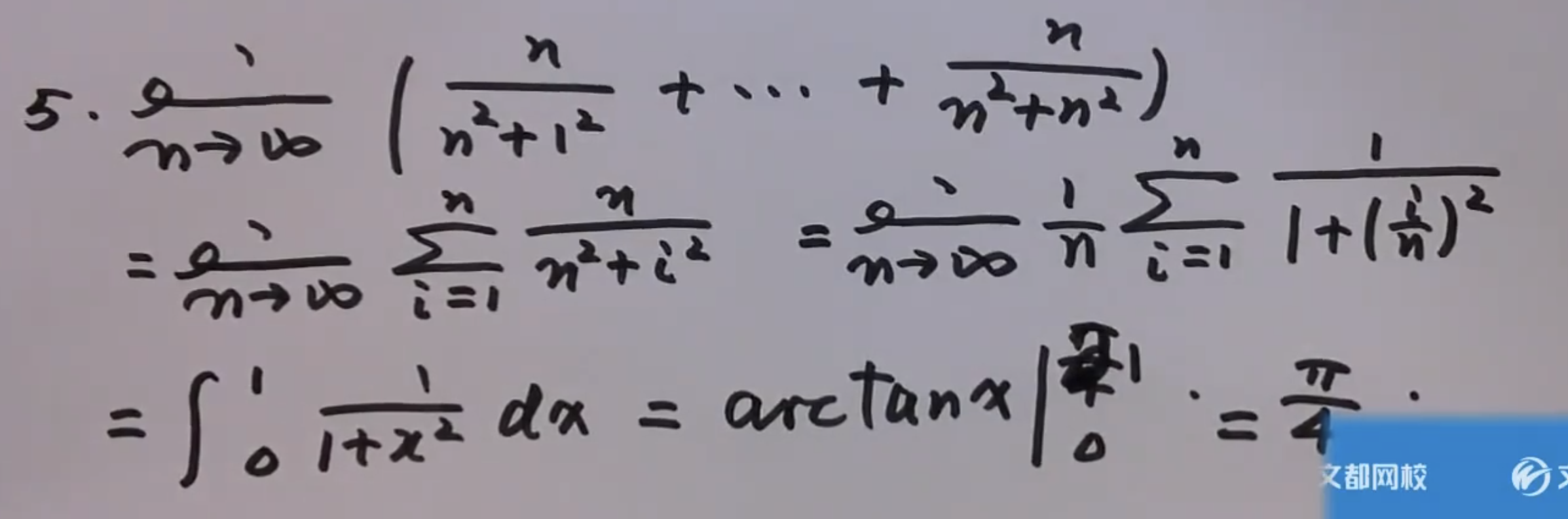
型二
证明极限存在
notes 

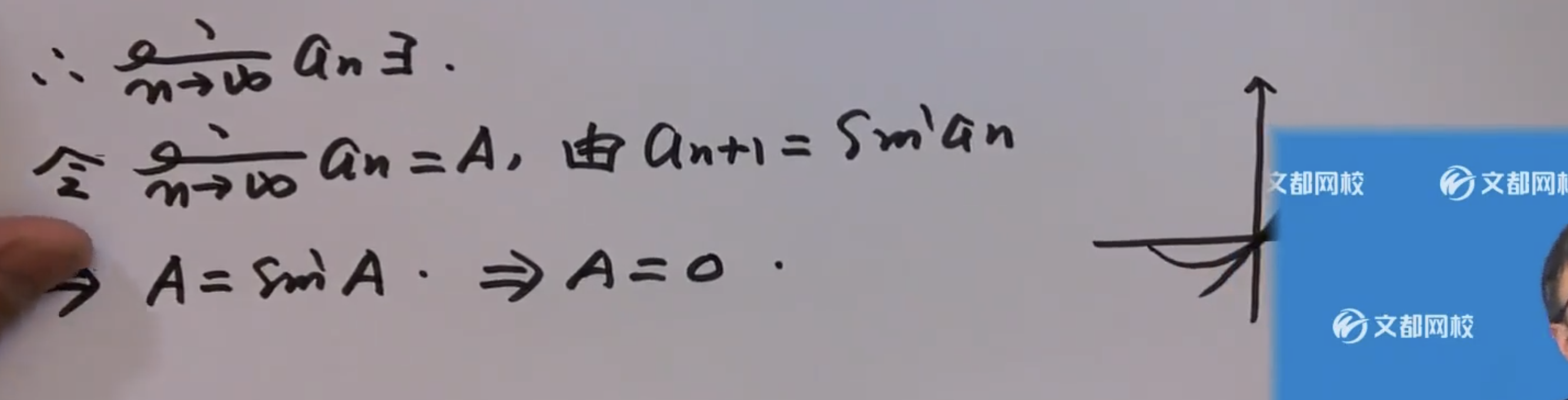


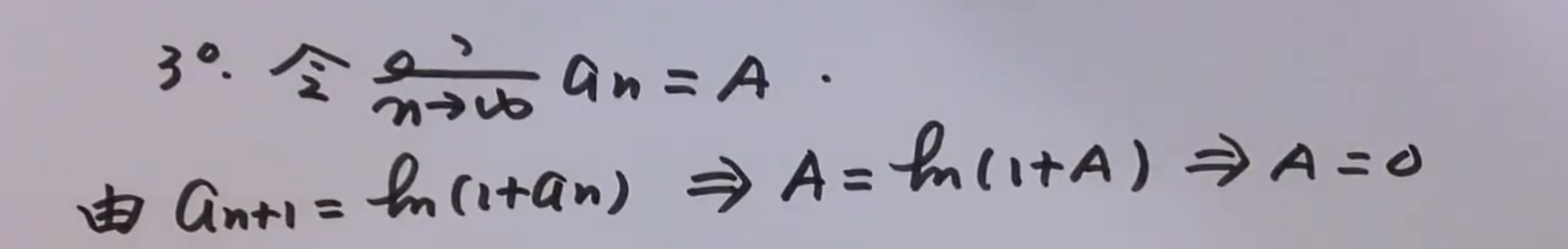

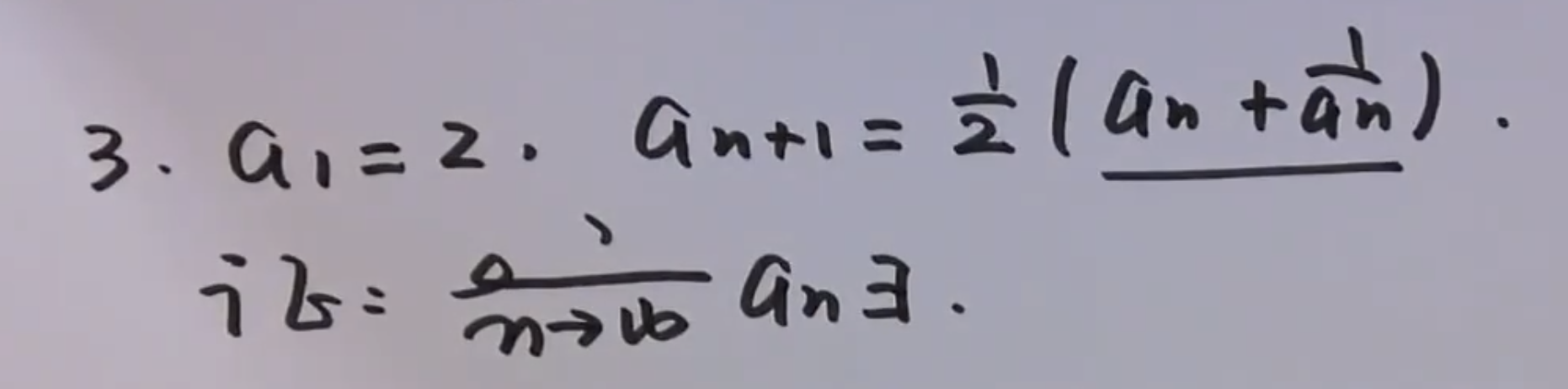
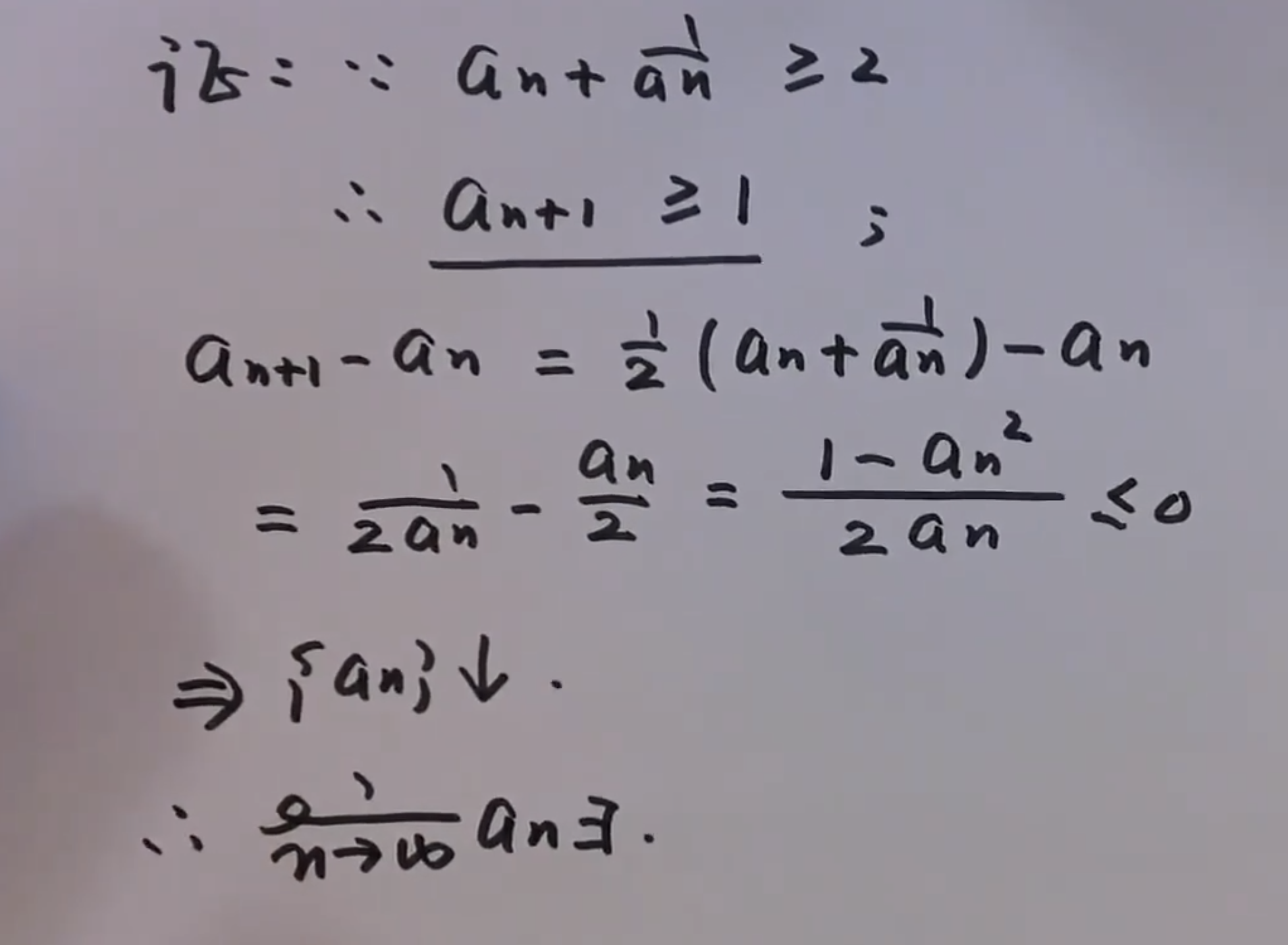
型三
不定型
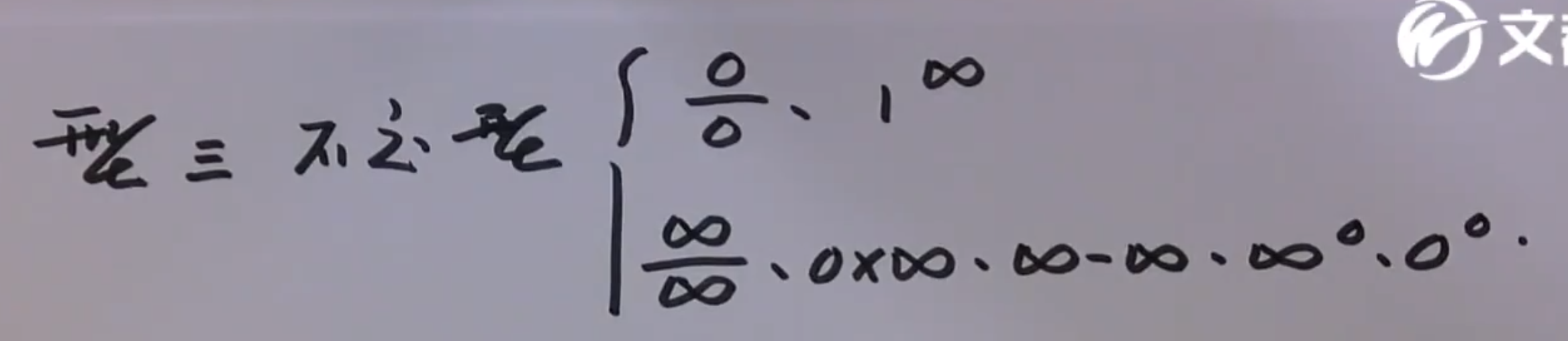


精度够可以用等价无穷小
0/0
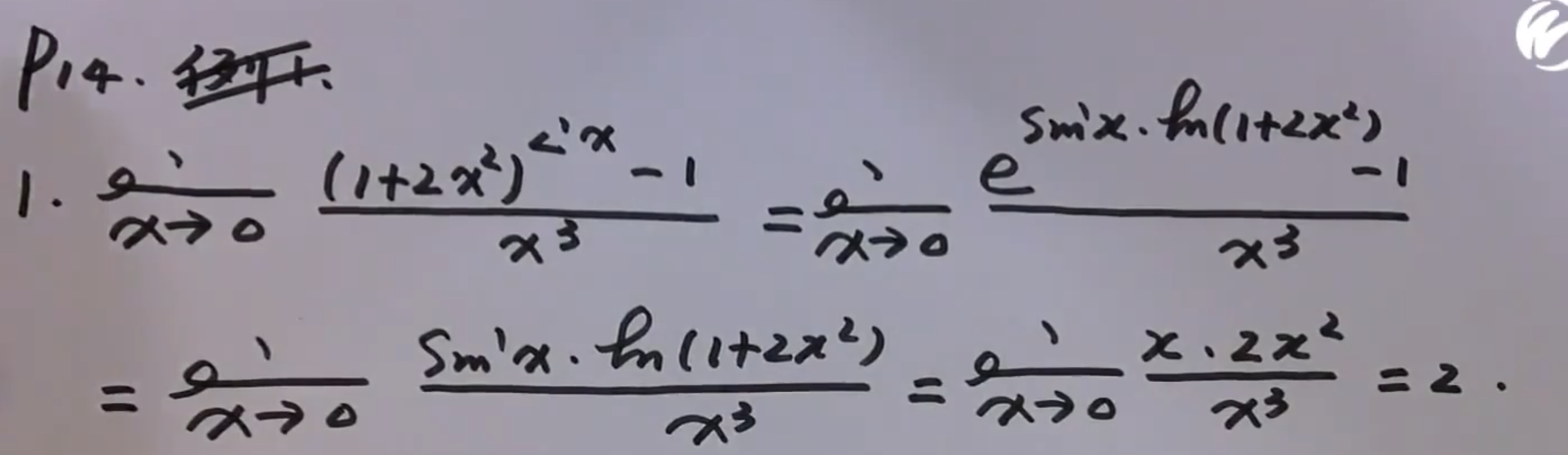

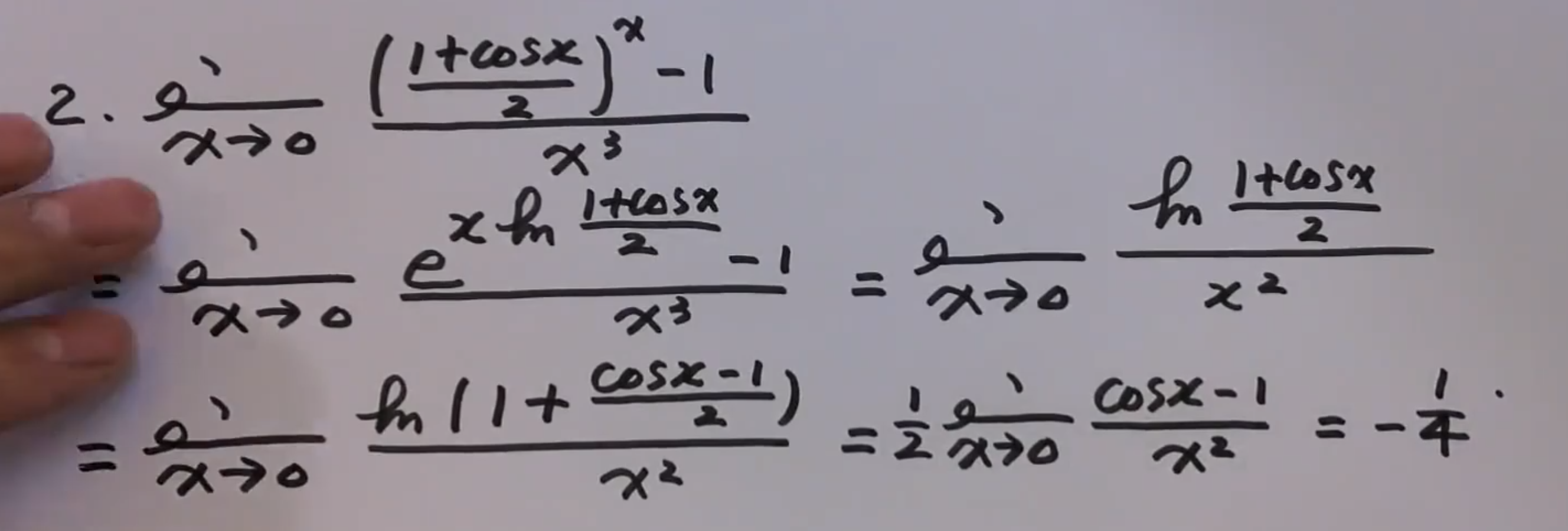
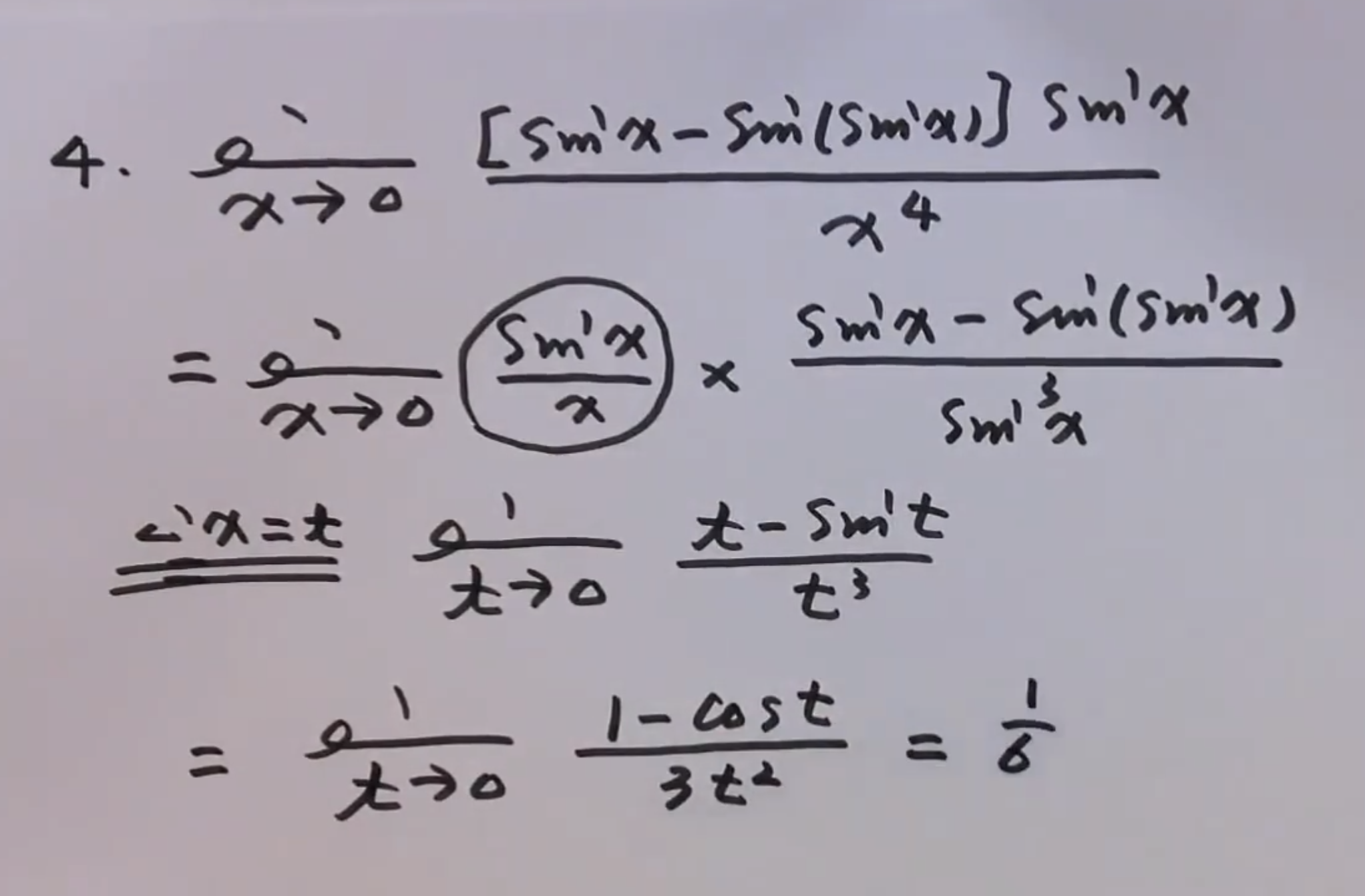
1的无穷大次方

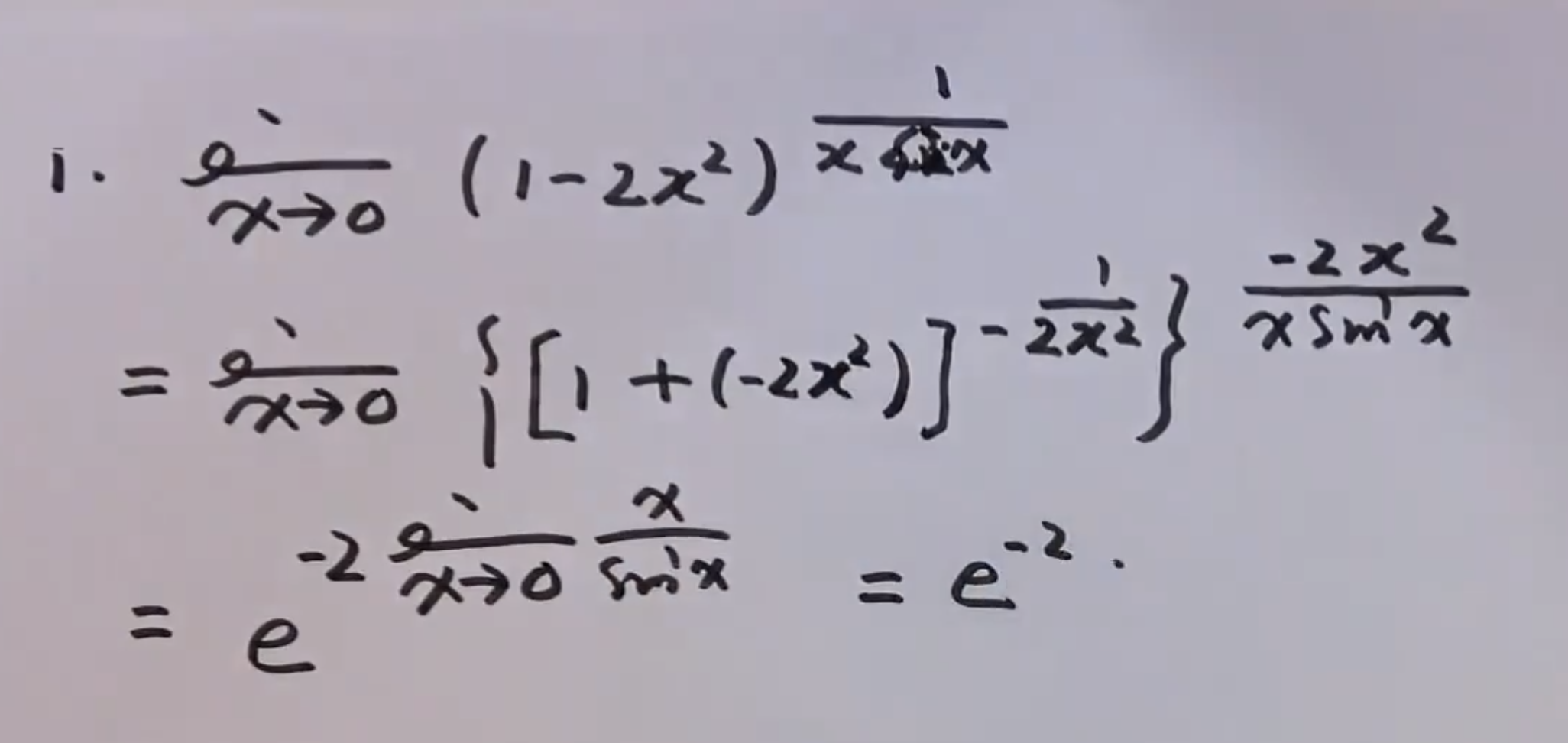
无穷/无穷
洛必达
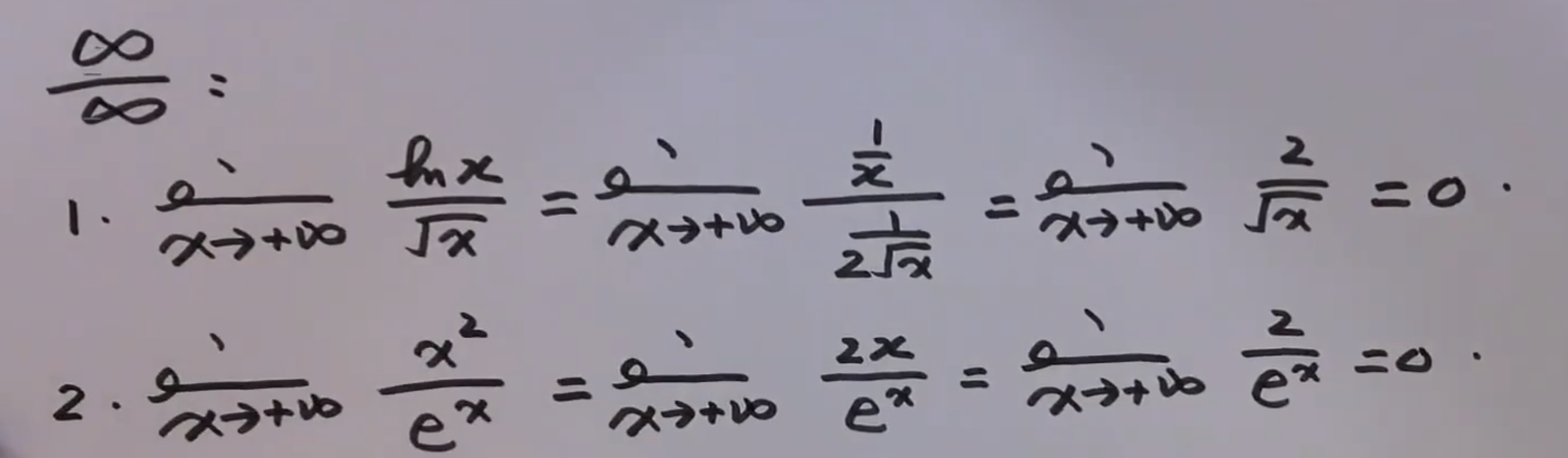
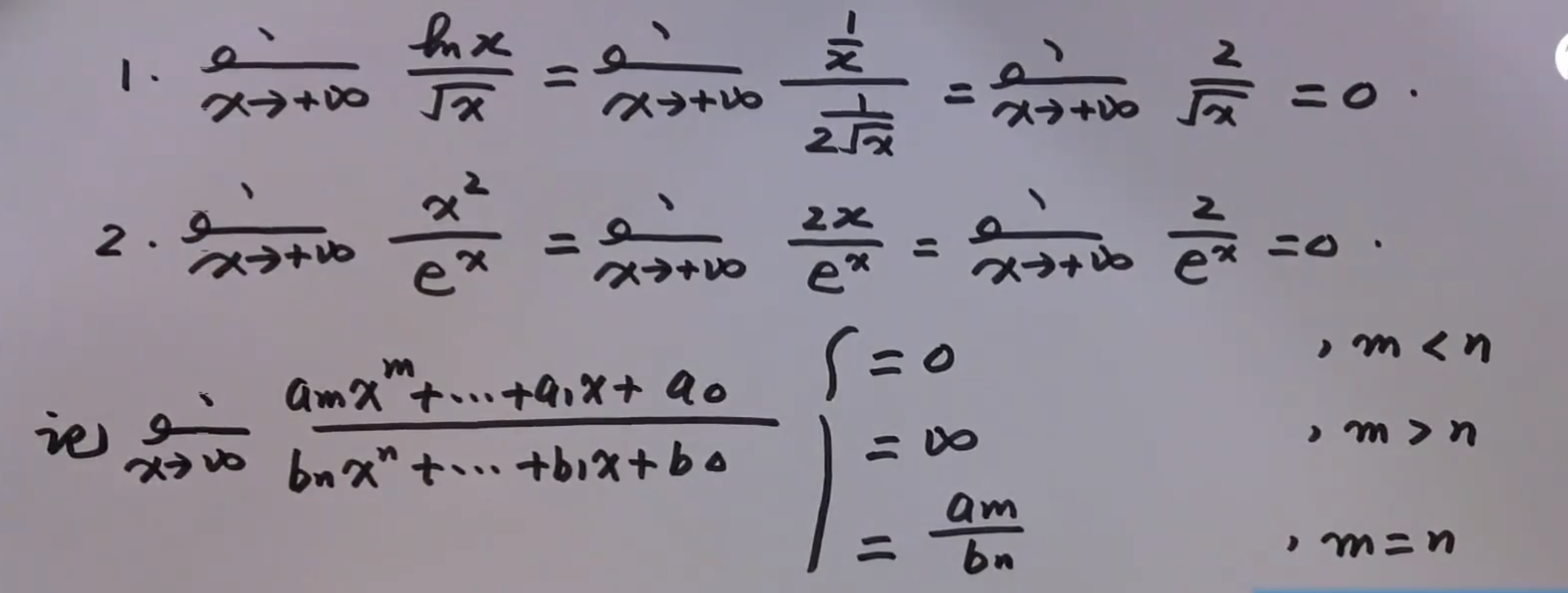
看不懂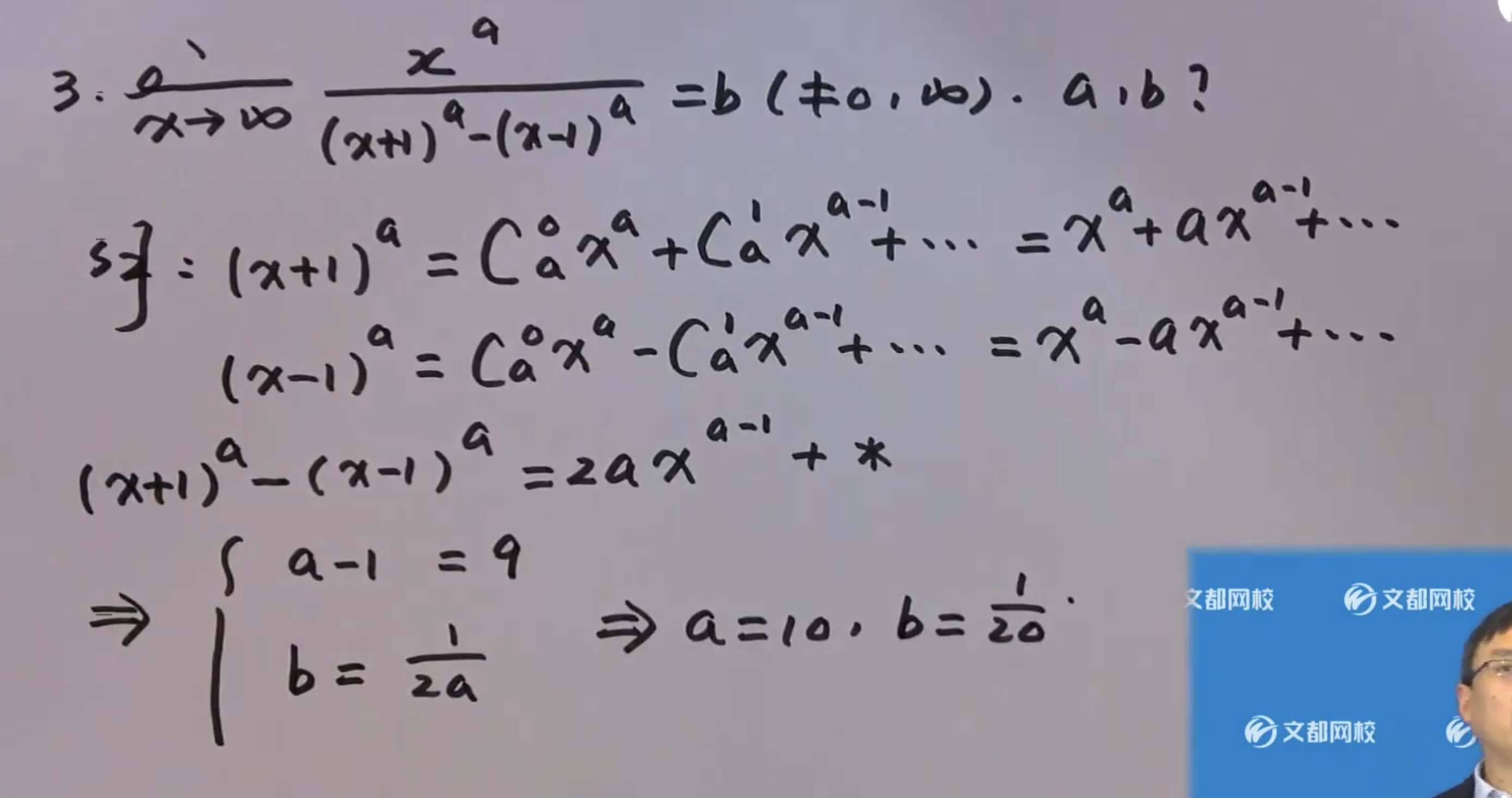
33:34
window.alert = function (obj) {
var iframe = document.createElement('iframe');
iframe.src = 'javascript:void(0);'
document.body.appendChild(iframe)
iframe.contentWindow.alert(obj);
iframe.parentNode.removeChild(iframe);
}
window.hugo={}
window.hugo.iframes=[]
let iframes=window.hugo.iframes;
var openIframe=function(html,body){
// 1. 创建<iframe>元素
var ifr = document.createElement('iframe');
// // 2. 将CSS,HTML字符串转换为Blob对象
// var blob = new Blob([html], {
// 'type': 'text/html'
// });
// // 3. 使用URL.createObjectURL()方法将...
// iframe.src = URL.createObjectURL(blob);
body.innerHTML = "";
body.appendChild(ifr);
var ifrw = (ifr.contentWindow) ? ifr.contentWindow: (ifr.contentDocument.document) ? ifr.contentDocument.document: ifr.contentDocument;
ifrw.document.open();
ifrw.document.write(html);
ifrw.document.close();
//console.log(x)
}
//开启页面html
{
let xx = $("#cnblogs_post_body,.cnblogs-post-body").find("[data-type=html]");
let xxx = [];
for (let x of xx) {
xxx.push(x.innerText)
};
xx.remove();
let URL = window.URL || window.webkitURL;
for (let x of xxx) {
//openIframe(x,document.body)
iframes.push(x);
};
}
等价无穷小

两个重要极限
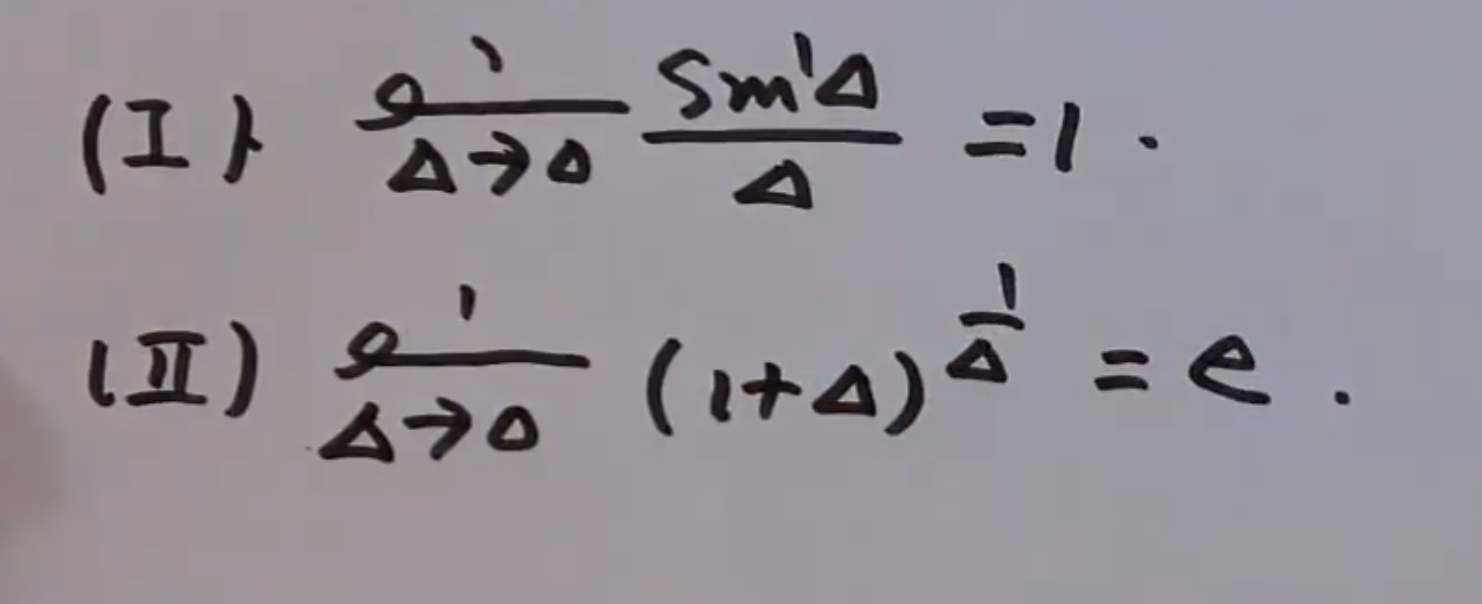
notes

型一
求极限题型
1)先求和

2)夹逼定理

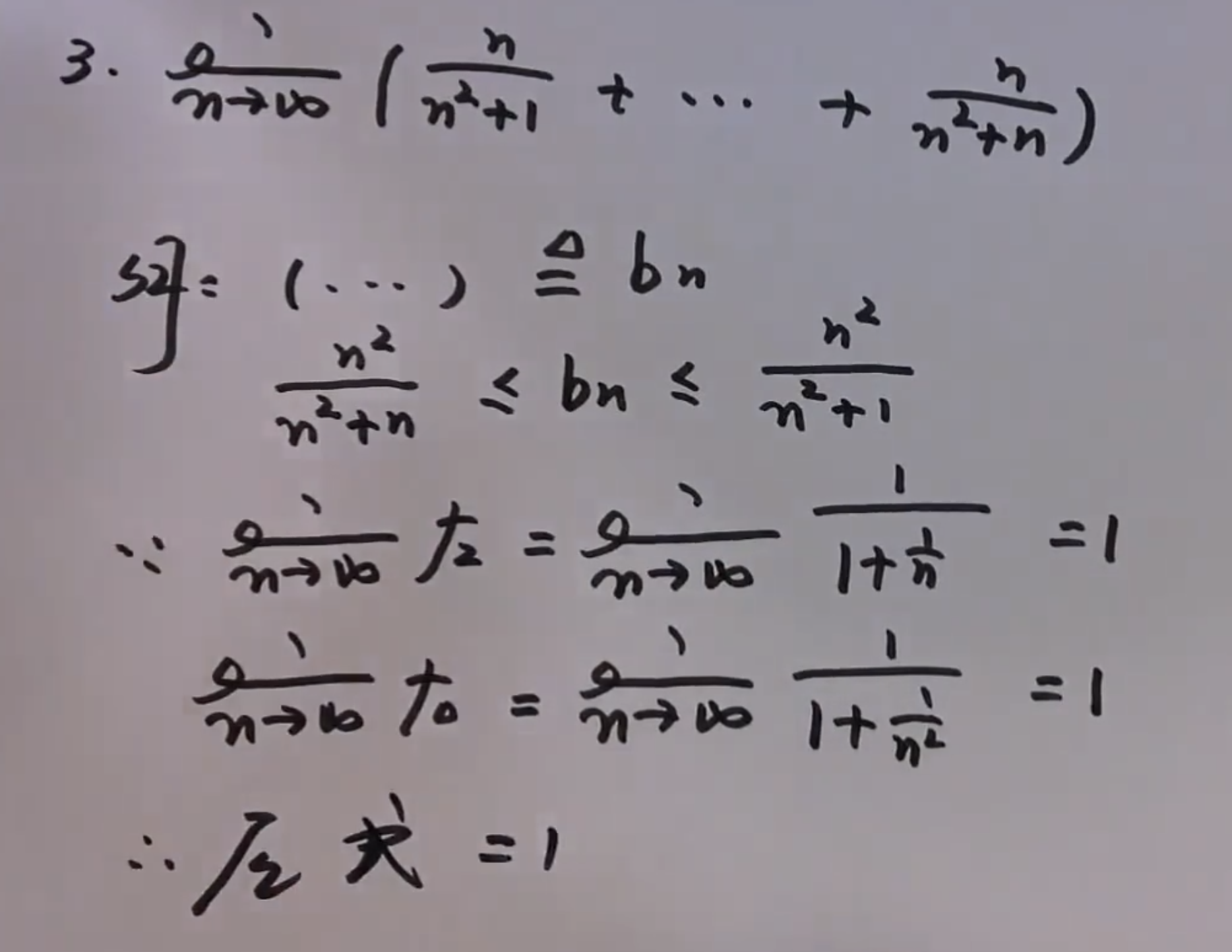
3)(重点)
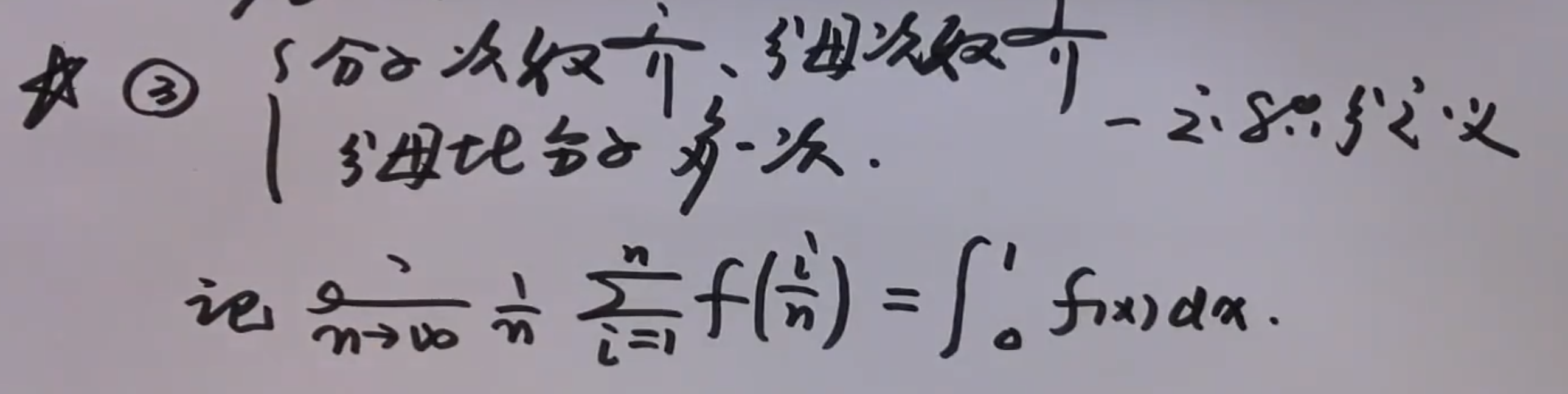
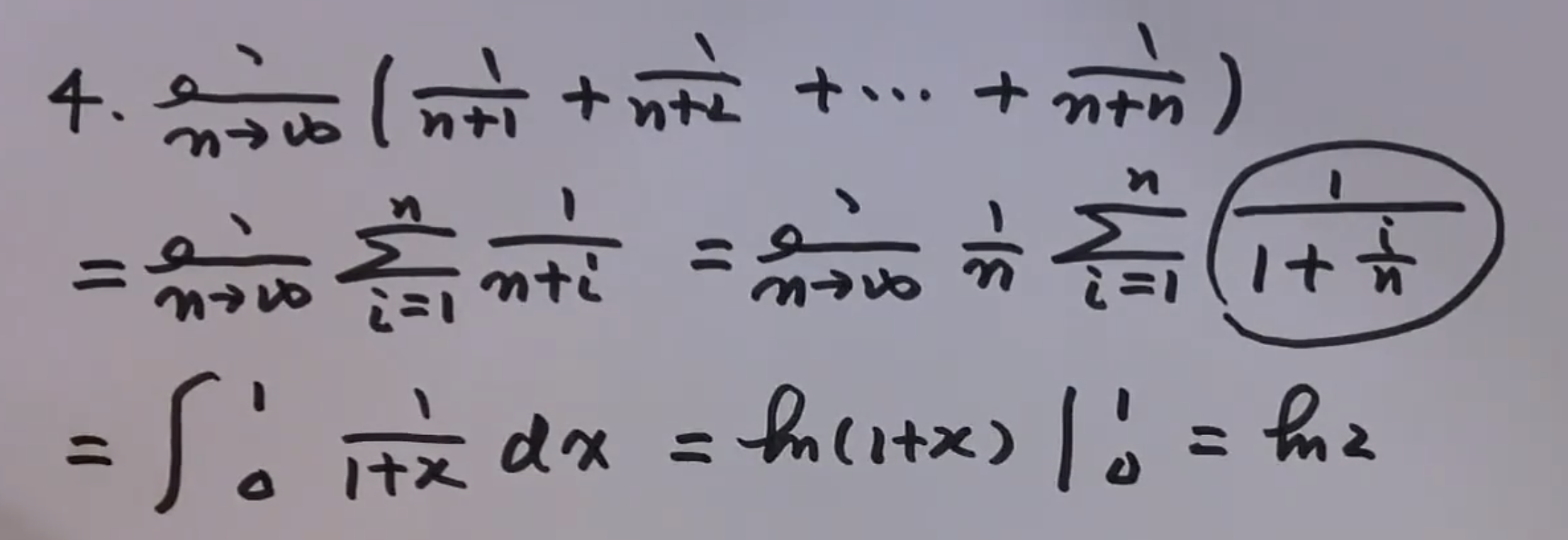
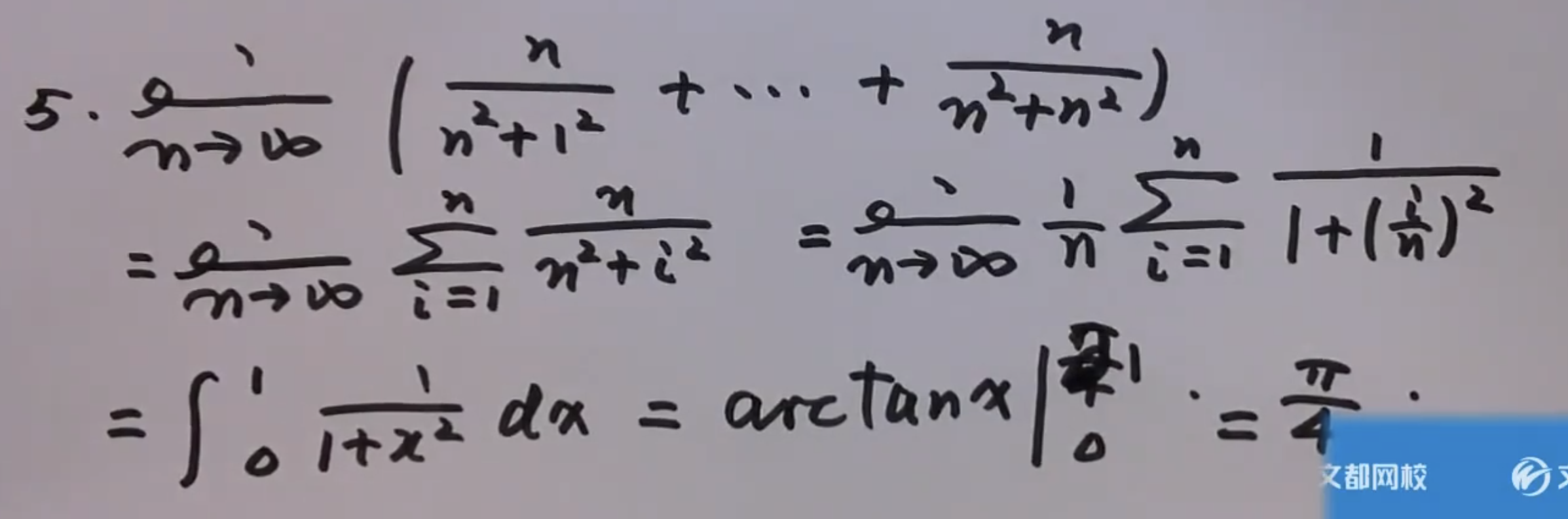
型二
证明极限存在
notes 

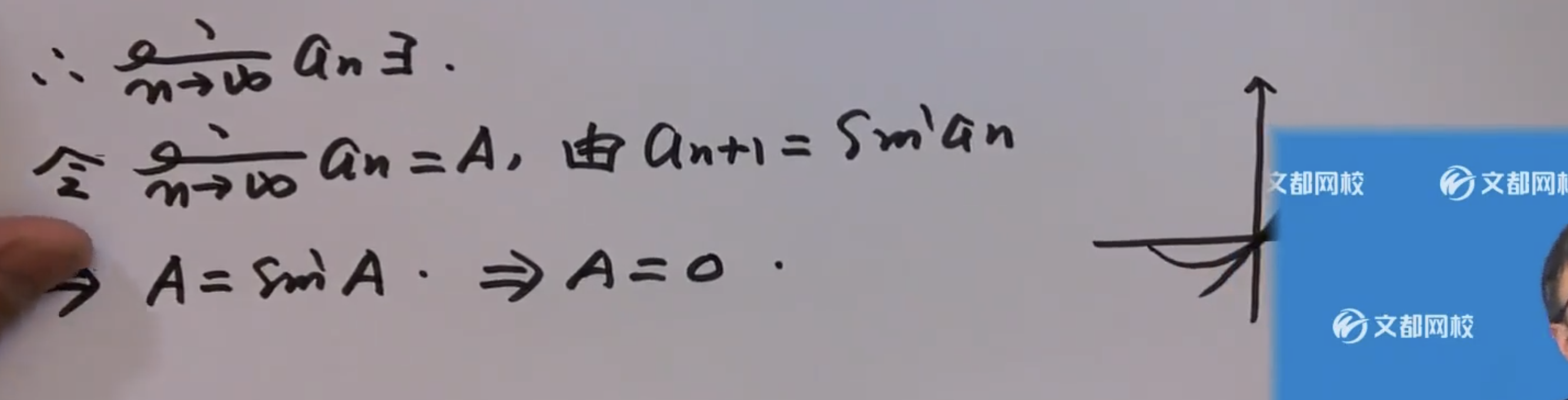


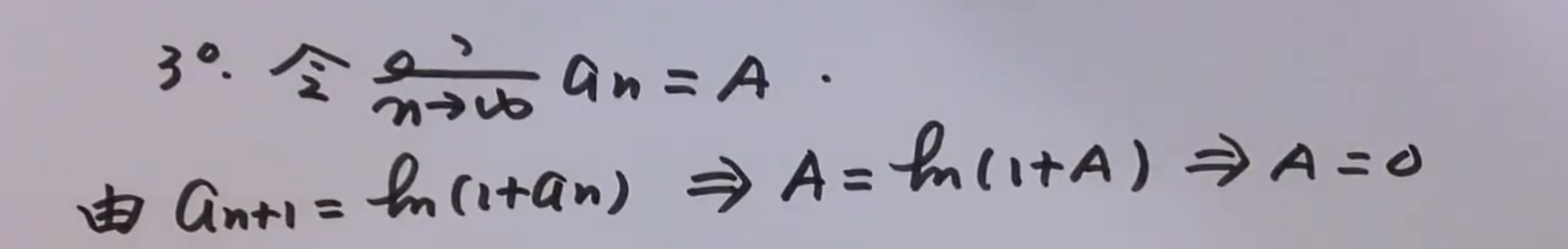

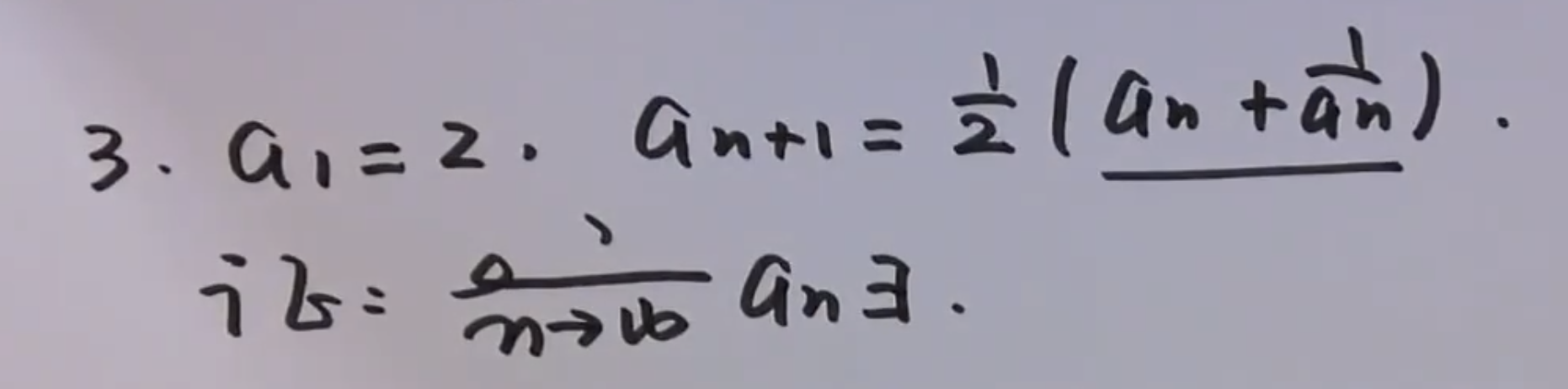
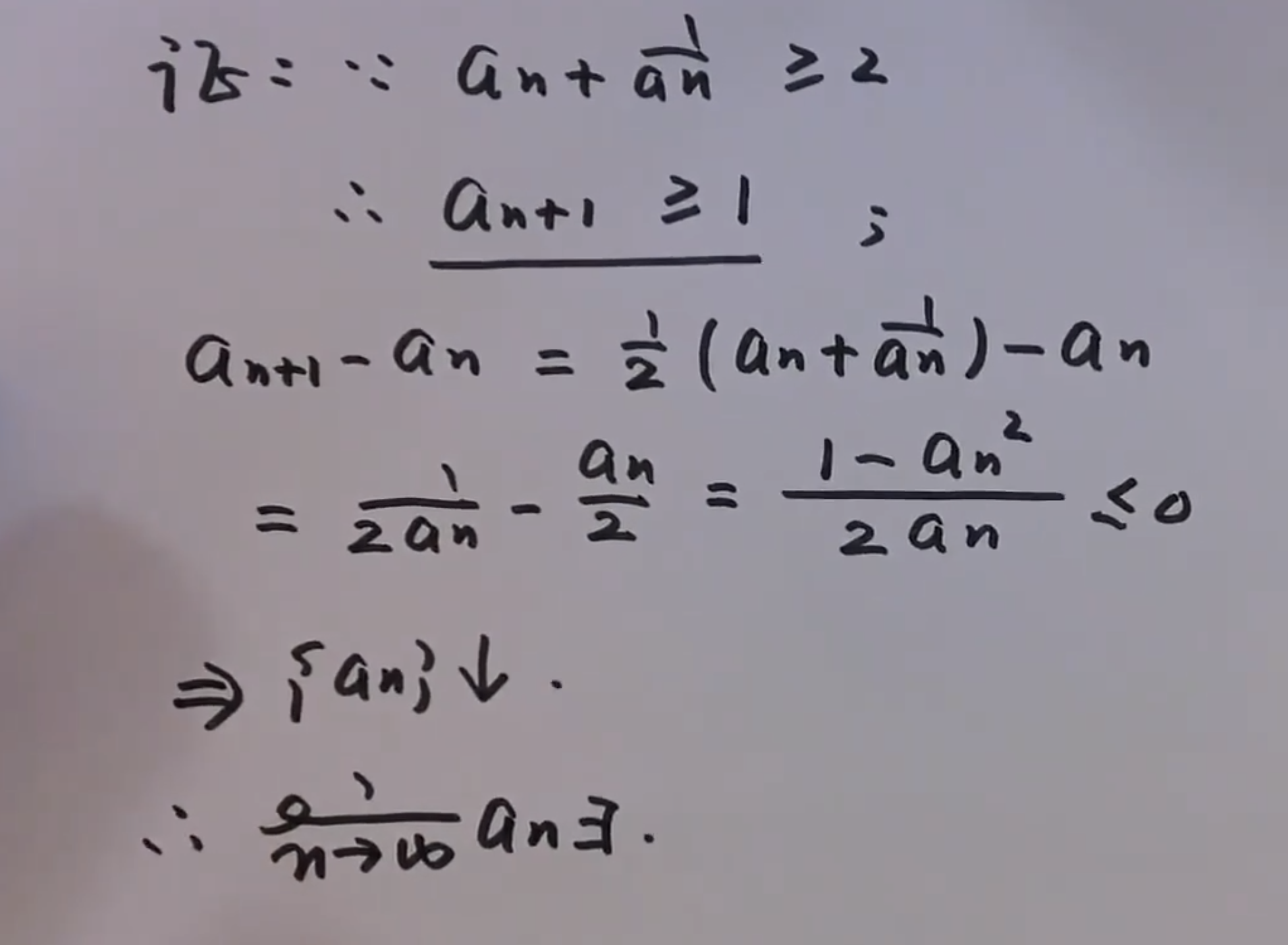
型三
不定型
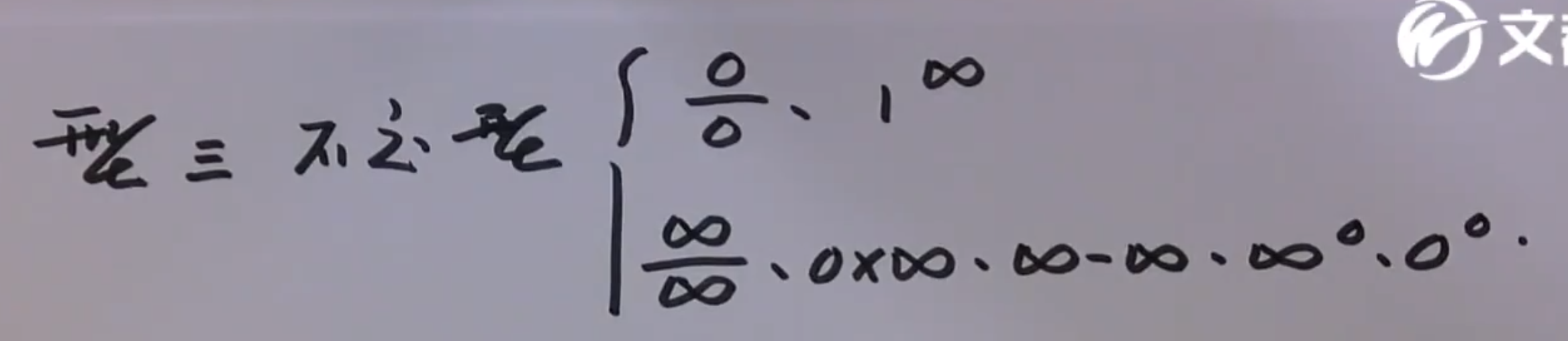


精度够可以用等价无穷小
0/0
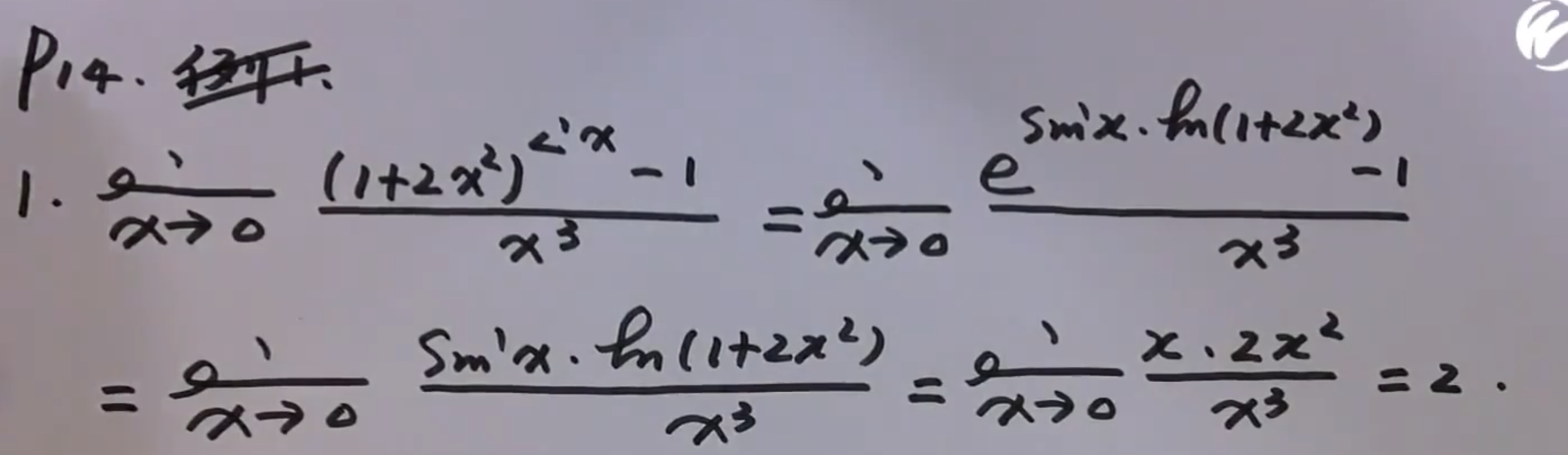

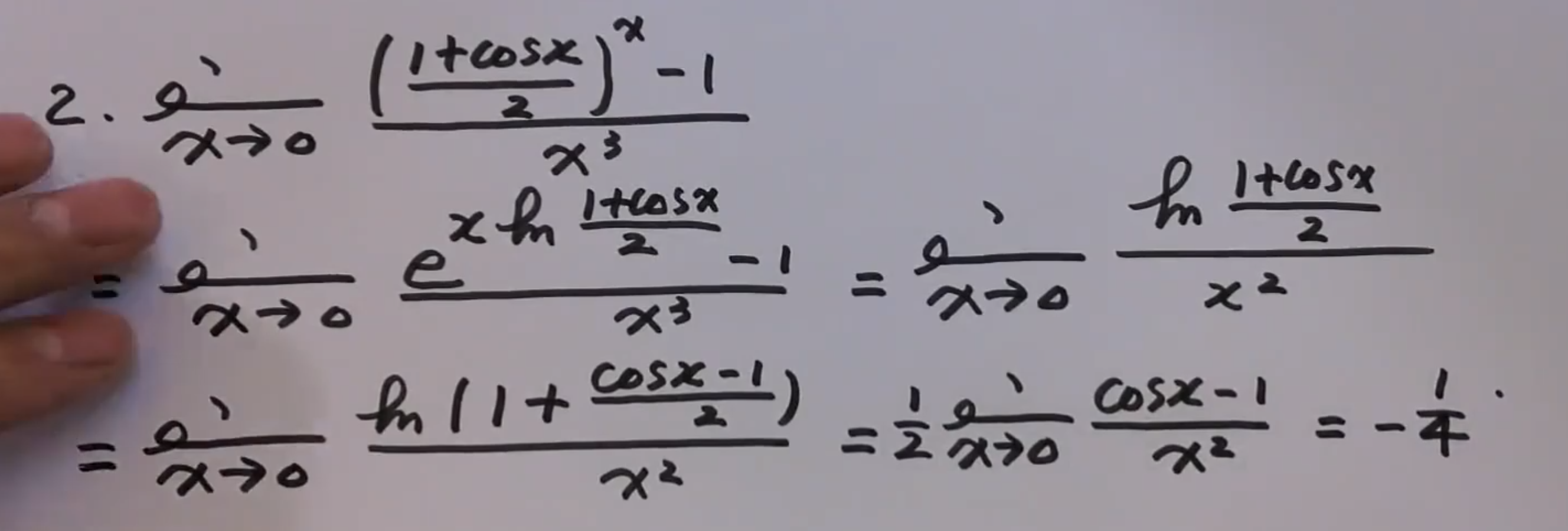
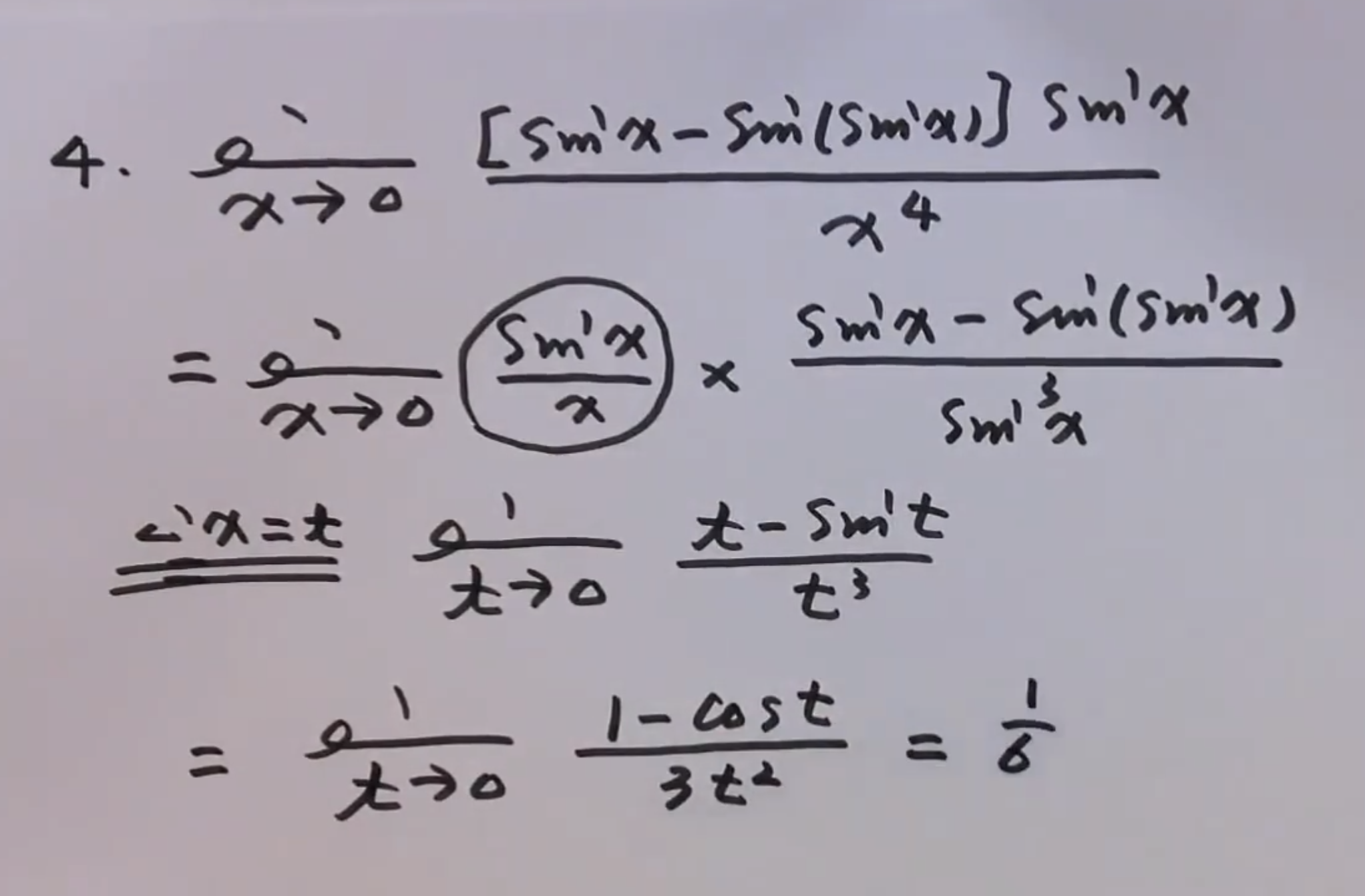
1的无穷大次方

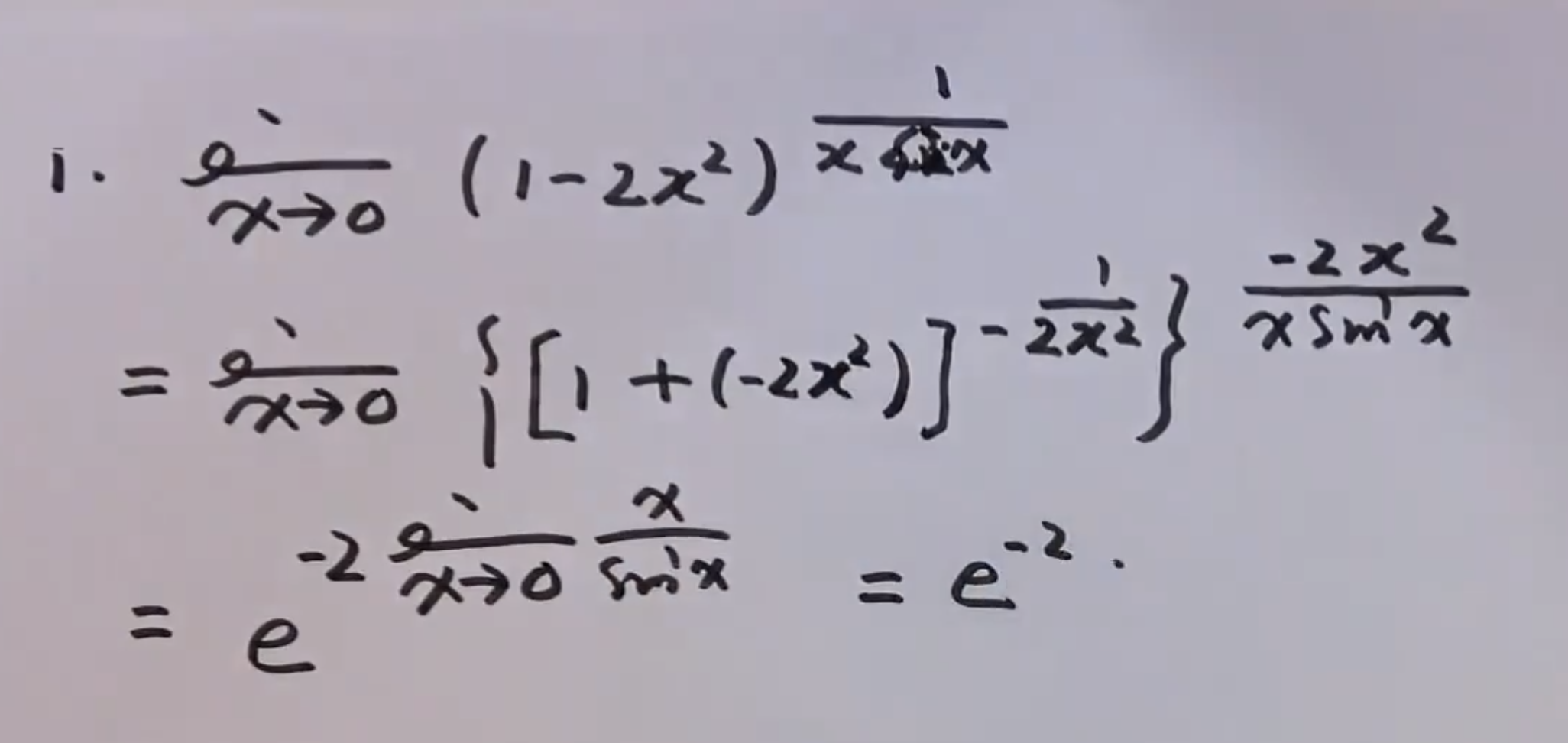
无穷/无穷
洛必达
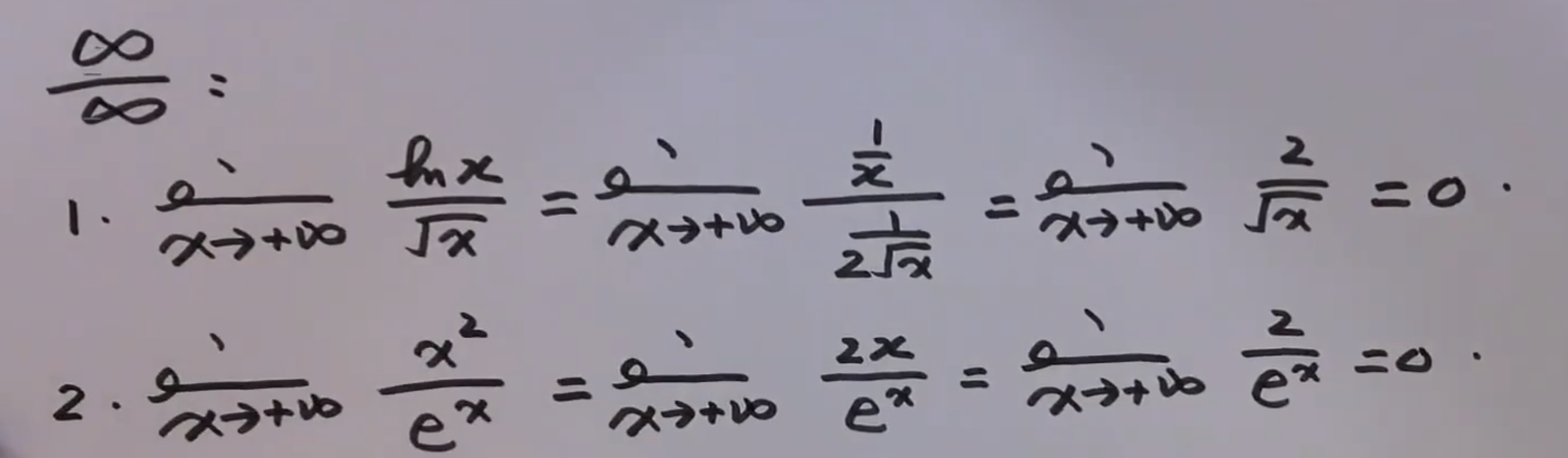
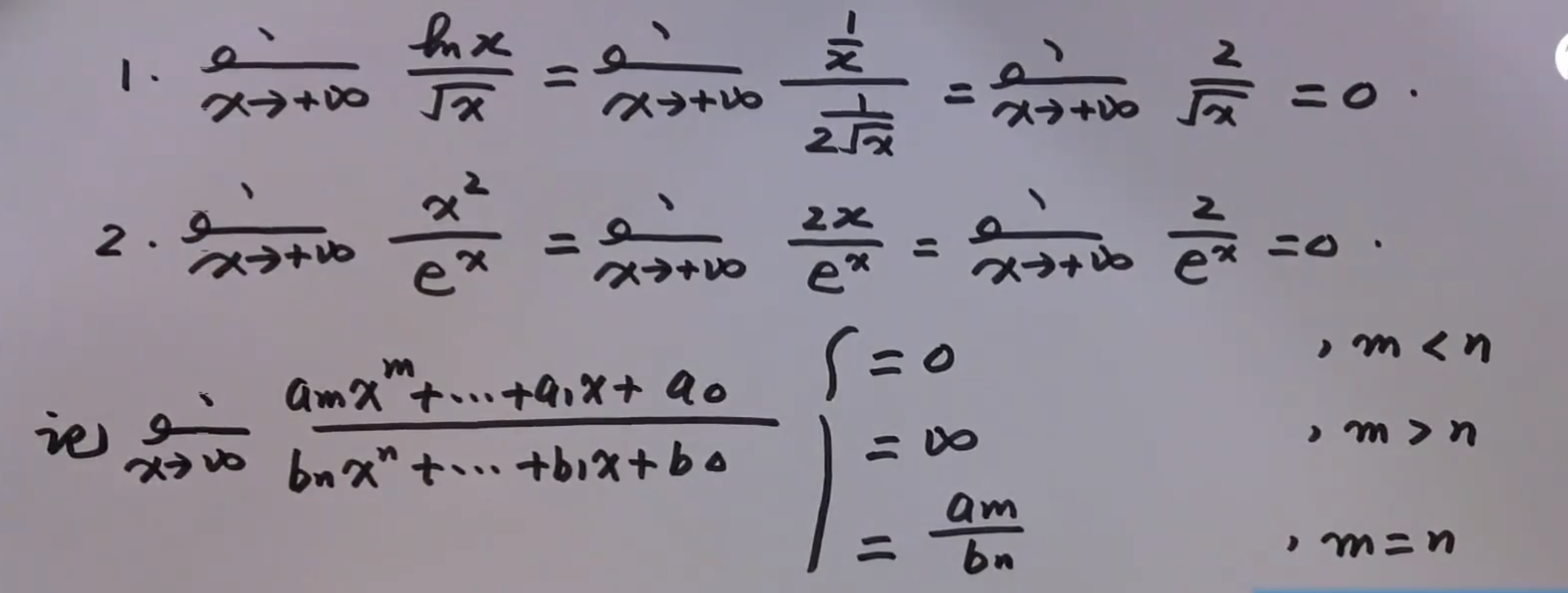
看不懂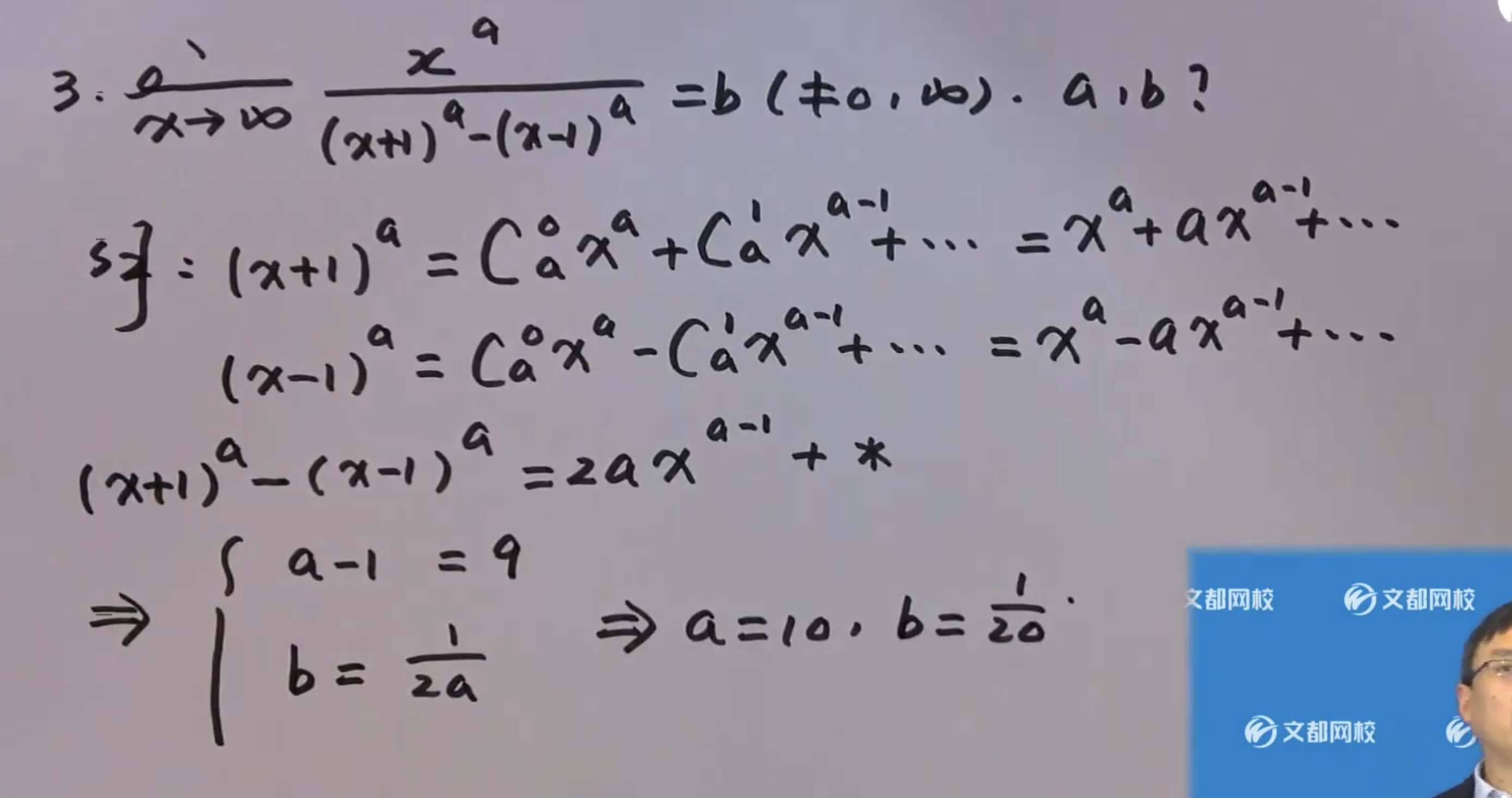
33:34

$(function() {
//修改粉丝数量
$("#profile_block a:eq(2)").html(parseInt(((new Date()).getTime()/1000-1555000000)/2))
//去广告
$("#ad_t2").remove()
$("#opt_under_post").remove()
$("#under_post_news").remove()
$("#cnblogs_c2").remove()
$("#cnblogs_c1").remove()
$("#HistoryToday").remove()
var kb=$("#under_post_kb")[0];
if(kb){
SOHUCS=document.createElement("div")
//SOHUCS=kb
SOHUCS.id="SOHUCS"
SOHUCS.setAttribute("sid",cb_blogId+"_"+cb_entryId)
kb.appendChild(SOHUCS)
}
})