Educational Codeforces Round 11
好久没写题了，现在回来重新写写题，马上就要开始省赛了，省赛不能别虐啊？
这套education还是很不错的，有很多值得注意的地方和东西。
A题：
题目：
You are given an array of n elements, you must make it a co-prime array in as few moves as possible.
In each move you can insert any positive integral number you want not greater than 109 in any place in the array.
An array is co-prime if any two adjacent numbers of it are co-prime.
In the number theory, two integers a and b are said to be co-prime if the only positive integer that divides both of them is 1.
The first line contains integer n (1 ≤ n ≤ 1000) — the number of elements in the given array.
The second line contains n integers ai (1 ≤ ai ≤ 109) — the elements of the array a.
Print integer k on the first line — the least number of elements needed to add to the array a to make it co-prime.
The second line should contain n + k integers aj — the elements of the array a after adding k elements to it. Note that the new array should be co-prime, so any two adjacent values should be co-prime. Also the new array should be got from the original array a by addingk elements to it.
If there are multiple answers you can print any one of them.
3
2 7 28
1
2 7 9 28
解题思路：
这道题就是说，我首先给你一个长度为n的数组，然后让你加k个数字加到这个数组中的任意位置，使得这个数组最终任意两两相邻的两个数都是互素的。由于n<=1000,我们知道，可以直接暴力就好了，就是枚举相邻的两个数字，然后判断gcd(a[i],a[i+1])==1，如果不等的话，就要在这个位置插入一个数字j,使得gcd(a[i],j)==1&&gcd(a[i+1],j)==1,那好，有了这样的条件后，我们只需要用O（n^2）的算法复杂度就可以对问题有个最终的解释了。 这道题一开始wa了，就是在枚举j的时候，一定要从j:1->max(a[i],a[i+1]),不要从j:min(a[i],a[i+1])->max(a[i],a[i+1]).数据中如果出现了两个连续相同的数字，那么就炸了。
代码：
1 # include <cstdio>
2 # include <iostream>
3 # include <vector>
4 using namespace std;
5 # define MAX 1234
6 int a[MAX],pos[MAX];
7 vector<int>res;
8 int gcd ( int a,int b )
9 {
10 if ( b==0 ) return a;
11 return gcd(b,a%b);
12 }
13 int main(void)
14 {
15 int n; cin>>n;
16 for ( int i = 0;i < n;i++ )
17 {
18 cin>>a[i];
19 }
20 int flag = 0;
21 int k = 0;
22 for ( int i = 0;i < n-1;i++ )
23 {
24 flag = 0;
25 if ( gcd(a[i],a[i+1])!=1 )
26 {
27 k++;
28 res.push_back(a[i]);
29 flag = 1;
30 for ( int j = 1;j < max(a[i],a[i+1]);j++ )
31 {
32 if ( (gcd(a[i],j)==1)&&(gcd(j,a[i+1])==1) )
33 {
34 res.push_back(j);
35 break;
36 }
37 }
38 }
39 if ( flag ) continue;
40 res.push_back(a[i]);
41 }
42 res.push_back(a[n-1]);
43 cout<<k<<endl;
44 for ( int i = 0;i < res.size();i++ )
45 {
46 cout<<res[i]<<" ";
47 }
48 cout<<endl;
49 return 0;
50 }
B题：
题目 ：
Consider 2n rows of the seats in a bus. n rows of the seats on the left and n rows of the seats on the right. Each row can be filled by two people. So the total capacity of the bus is 4n.
Consider that m (m ≤ 4n) people occupy the seats in the bus. The passengers entering the bus are numbered from 1 to m (in the order of their entering the bus). The pattern of the seat occupation is as below:
1-st row left window seat, 1-st row right window seat, 2-nd row left window seat, 2-nd row right window seat, ... , n-th row left window seat, n-th row right window seat.
After occupying all the window seats (for m > 2n) the non-window seats are occupied:
1-st row left non-window seat, 1-st row right non-window seat, ... , n-th row left non-window seat, n-th row right non-window seat.
All the passengers go to a single final destination. In the final destination, the passengers get off in the given order.
1-st row left non-window seat, 1-st row left window seat, 1-st row right non-window seat, 1-st row right window seat, ... , n-th row left non-window seat, n-th row left window seat, n-th row right non-window seat, n-th row right window seat.
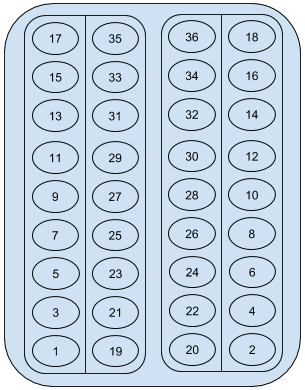The seating for n = 9 and m = 36.You are given the values n and m. Output m numbers from 1 to m, the order in which the passengers will get off the bus.
The only line contains two integers, n and m (1 ≤ n ≤ 100, 1 ≤ m ≤ 4n) — the number of pairs of rows and the number of passengers.
Print m distinct integers from 1 to m — the order in which the passengers will get off the bus.
2 7
5 1 6 2 7 3 4
9 36
19 1 20 2 21 3 22 4 23 5 24 6 25 7 26 8 27 9 28 10 29 11 30 12 31 13 32 14 33 15 34 16 35 17 36 18
解题思路：
这道题就是个水模拟，题意只要读清楚就行了，就是说，一开始我有4*n个数字，然后一开始这些数字被按照一定的顺序存放着，接下来，我们给一个m，表示的是要出去多少个数，
然后打印出这m个数字。看到了4列，我首先想到的就是用队列来模拟这个题目，那么开了4个队列分别模拟每一列，然后每次依据先进先出的原则直到最后取完了m个数字后，我们就得
到了最后要打印的序列。
代码：
1 # include <cstdio> 2 # include <iostream> 3 # include <vector> 4 # include <queue> 5 using namespace std; 6 queue<int>v1,v2,v3,v4; 7 int main(void) 8 { 9 int n,m; cin>>n>>m; 10 int a0 = 1; 11 int tmp; 12 for ( int i = 0;i < n;i++ ) 13 { 14 tmp = a0+i*2; 15 v1.push(tmp); 16 } 17 a0 = tmp+2; 18 for ( int i = 0;i < n;i++ ) 19 { 20 v2.push(a0+i*2); 21 } 22 a0++; 23 for ( int i = 0;i < n;i++ ) 24 { 25 v3.push(a0+i*2); 26 } 27 a0 = 2; 28 for ( int i = 0;i < n;i++ ) 29 { 30 v4.push(a0+i*2); 31 } 32 int cnt = 0; 33 for ( int i = 0;;i++ ) 34 { 35 if ( cnt==m ) 36 break; 37 if ( i%4==0 ) 38 { 39 int cur = v2.front(); 40 if ( cur > m ) continue; 41 cout<<v2.front()<<" "; 42 v2.pop(); 43 cnt++; 44 } 45 else if ( i%4==1 ) 46 { 47 int cur = v1.front(); 48 if ( cur > m ) continue; 49 cout<<v1.front()<<" "; 50 v1.pop(); 51 cnt++; 52 } 53 else if ( i%4==2 ) 54 { 55 int cur = v3.front(); 56 if ( cur > m ) continue; 57 cout<<v3.front()<<" "; 58 v3.pop(); 59 cnt++; 60 } 61 else if ( i%4==3 ) 62 { 63 int cur = v4.front(); 64 if ( cur > m ) continue; 65 cout<<v4.front()<<" "; 66 v4.pop(); 67 cnt++; 68 } 69 } 70 cout<<endl; 71 return 0; 72 }
C题：
题目：
You are given an array a with n elements. Each element of a is either 0 or 1.
Let's denote the length of the longest subsegment of consecutive elements in a, consisting of only numbers one, as f(a). You can change no more than k zeroes to ones to maximize f(a).
The first line contains two integers n and k (1 ≤ n ≤ 3·105, 0 ≤ k ≤ n) — the number of elements in a and the parameter k.
The second line contains n integers ai (0 ≤ ai ≤ 1) — the elements of a.
On the first line print a non-negative integer z — the maximal value of f(a) after no more than k changes of zeroes to ones.
On the second line print n integers aj — the elements of the array a after the changes.
If there are multiple answers, you can print any one of them.
7 1
1 0 0 1 1 0 1
4
1 0 0 1 1 1 1
10 2
1 0 0 1 0 1 0 1 0 1
5
1 0 0 1 1 1 1 1 0 1
解题思路：
这道题是说，我现在有一个长度为n的只含有0和1的数列，然后一个数字k，我们最多只能将k个0改成1，那么求出连续最长的1的子序列，并且打印输出。
解法方面，我们首先肯定是先从左到右统计0的个数，然后变统计变更新。每次都记录这个区间最多的1的个数。
代码：
1 # include <cstdio> 2 # include <iostream> 3 using namespace std; 4 # define MAX 323456 5 # define inf 99999999 6 int a[MAX]; 7 int main(void) 8 { 9 int n,k; cin>>n>>k; 10 int res = -inf; 11 for ( int i = 0;i < n;i++ ) 12 { 13 cin>>a[i]; 14 } 15 int cnt_0 = 0; 16 int pos1, pos2; 17 int l = 0; 18 for ( int i = 0;i < n;i++ ) 19 { 20 if ( a[i]==0 ) cnt_0++; 21 while ( cnt_0 > k ) 22 { 23 if ( a[l]==0 ) cnt_0--; 24 l++; 25 } 26 if ( i-l > res ) 27 { 28 res = i-l; 29 pos1 = i; 30 pos2 = l; 31 } 32 } 33 for ( int i = pos2;i <= pos1;i++ ) 34 { 35 a[i] = 1; 36 } 37 cout<<pos1-pos2+1<<endl; 38 for ( int i = 0;i < n;i++ ) 39 { 40 if ( i!=0 ) cout<<" "; 41 cout<<a[i]; 42 } 43 return 0; 44 }
