二分·归并排序之逆序对 算法讲解和题目

题目：

　　

#1141 : 二分·归并排序之逆序对

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在上一回、上上回以及上上上回里我们知道Nettle在玩《艦これ》。经过了一番苦战之后，Nettle又获得了的很多很多的船。
这一天Nettle在检查自己的舰队列表：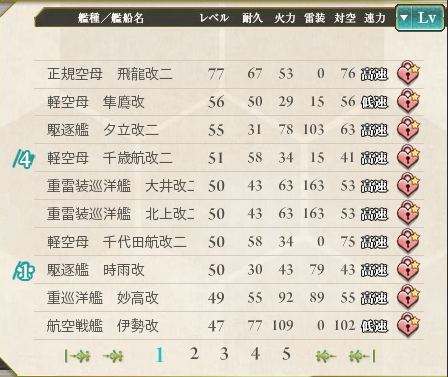

我们可以看到，船默认排序是以等级为参数。但实际上一个船的火力值和等级的关系并不大，所以会存在A船比B船等级高，但是A船火力却低于B船这样的情况。比如上图中77级的飞龙改二火力就小于55级的夕立改二。
现在Nettle将按照等级高低的顺序给出所有船的火力值，请你计算出一共有多少对船满足上面提到的这种情况。

提示：火力高才是猛！

输入

第1行：1个整数N。N表示舰船数量, 1≤N≤100,000
第2行：N个整数，第i个数表示等级第i低的船的火力值a[i]，1≤a[i]≤2^31-1。

输出

第1行：一个整数，表示有多少对船满足“A船比B船等级高，但是A船火力低于B船”。

样例输入

10
1559614248 709366232 500801802 128741032 1669935692 1993231896 369000208 381379206 962247088 237855491

样例输出

27

解题思路：

　　这个题就是说求解逆序对的个数，我们以前就知道关于逆序数的问题，我们可以通过bit（树状数组）来求解，如果不知道树状数组的可以自行百度一发，其实BIT就两个非常重要的操作，一个是求区间的和，一个是单点修改操作，这两个操作理解透彻了，剩下的东西都是非常容易弄明白的。

　　那么这个题，我们没有用最开始的BIT去做，我是借鉴了ACdreamer的博客，然后使用归并排序来解决这个问题。实际上，归并排序过程中，交换的次数其实就是这个数组中逆序对的个数。我们可以这样考虑，

有一个数组a[lo...hi],那么归并排序实际上就是将数组分成a[lo...mid]和a[mid+1...hi]这样的形式，然后分别归并排序，最后再将其合并起来的过程。在合并的过程中（lo<=i<=mid, mid+1<=j<=hi），当a[i]<=a[j]的时候，这个时候的并不会产生逆序数。当a[i]>a[j]的时候，这个时候就会产生逆序数了。因为在a[i]后面比a[i]大的数字都会比a[j]大，并且假设这个时候merge_sort(lo,mid)已经是一个有序的部分了。那么现在将a[j]放到a[i]的前面的话，逆序数就好增加ans+=mid+1-i个。因此我们可以边归并，边计算。

代码：

# include <cstdio>
# include <iostream>
using namespace std;
# define MAX 123456
int a[MAX],res[MAX];
long long ans = 0;
void Merge( int lo,int mid,int hi )
{
    if ( hi < lo ) return;
    int i = lo;
    int j = mid+1;
    int k = lo;
    while ( i <= mid&& j <= hi )
    {
        if ( a[i] > a[j] )
        {
            res[k++] = a[j++];
            ans+=mid+1-i;
        }
        else
        {
            res[k++] = a[i++];
        }
    }
    while ( i <= mid )
    {
        res[k++] = a[i++];
    }
    while ( j <= hi )
    {
        res[k++] = a[j++];
    }
    for ( int i = lo;i <= hi;i++ )
    {
        a[i] = res[i];
    }
}
void Merge_sort( int lo,int hi )
{
    if ( lo < hi )
    {
        int mid = (lo+hi)>>1;
        Merge_sort(lo,mid);
        Merge_sort(mid+1,hi);
        Merge(lo,mid,hi);
    }
}
int main(void)
{
    int n; cin>>n;
    for ( int i = 0;i < n;i++ )
    {
        cin>>a[i];
    }
    Merge_sort(0,n-1);
    cout<<ans<<endl;
    return 0;
}