汉诺塔递归问题
递归（recursion）：
程序调用自身的编程技巧。把问题转化为规模缩小了的同类问题的子问题。然后递归调用函数(或过程)来表示问题的解
递归满足2个条件：
1）有反复执行的过程（调用自身）
2）有跳出反复执行过程的条件（递归出口）
如何思考递归（此段摘于qmdweb的CSDN博客）
在初学递归的时候, 看到一个递归实现, 我们总是难免陷入不停的验证之中，比如上面提及的阶乘，求解Factorial(n)时，我们总会情不自禁的发问，Factorial(n-1)可以求出正确的答案么？接着我们就会再用Factorial(n-2)去验证，，，不停地往下验证直到Factorial(0)。
对递归这样的不适应，和我们平时习惯的思维方式有关。我们习惯的思维是：已知Factorial(0)，乘上 1 就等于Factorial(1)，再乘以 2 就等于Factorial(2)，，，直到乘到 n。
而递归和我们的思维方式正好相反。
那我们怎么判断这个递归计算是否是正确的呢？Paul Graham 提到一种方法，如下：
如果下面这两点是成立的，我们就知道这个递归对于所有的 n 都是正确的。
当 n=0,1 时，结果正确；
假设递归对于 n 是正确的，同时对于 n+1 也正确。
这种方法很像数学归纳法，也是递归正确的思考方式，上述的第 1 点称为基本情况，第 2 点称为通用情况。
在递归中，我们通常把第 1 点称为终止条件，因为这样更容易理解，其作用就是终止递归，防止递归无限地运行下去。
汉诺塔问题描述为：
有三根杆子 A，B，C。A 杆上有 N 个穿孔圆盘，盘的尺寸由上到下依次变大，B，C 杆为空。要求按下列规则将所有圆盘移至 C 杆：
每次只能移动一个圆盘，大盘不能叠在小盘上面。
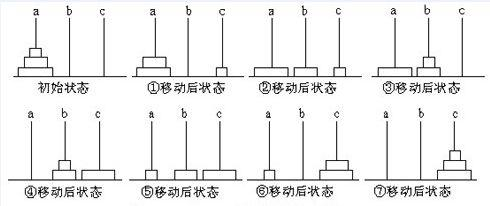
思路（如何移？最少要移动多少次？）
首先看下基本情况，即终止条件：N=1 时，直接从 A 移到 C。
再来看下通用情况：当有 N 个圆盘在 A 上（N>1），我们怎么移动 N个圆盘到 C 杠上呢？很简单，我们首先用将 N-1个圆盘移动到 C 上的方法将 N 个圆盘都移动到 B 上，然后再把第 N个圆盘（只有一个）移动到 C 上，再用同样的方法将在 B 杠上的 N -1个圆盘移动到 C 上，问题解决。
Python代码实现 （3个盘子移动过程如下） 与C语言类似
def hanoi(n,a,b,c):
if n==1 :
print(a,'->',c)
else :
hanoi(n-1,a,c,b)
hanoi(1,a,b,c)
hanoi(n-1,b,a,c)
hanoi(3,'A','B','C')
