树-哈夫曼编码

哈夫曼树（最优二叉树）

每个叶子节点都有权值，权值越大的叶节点越靠近根节点，而权值越小的叶节点越远离根节点

建立规则：

依据给出的n个权值，选择最小的两个权值作为一棵新的二叉树的左右子树，并且新的根节点的权值为左右子树权值之和

将新根节点与剩下的有权值的节点重复此操作直至只剩一个根节点

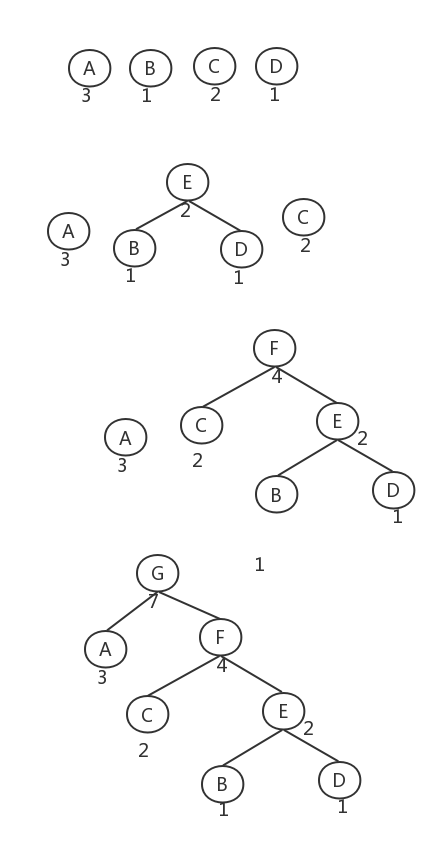
哈夫曼编码：

在哈夫曼树的基础上，规定哈夫曼树中的左分支代表0，右分支代表1，从根节点到每个叶节点所经过的路径分支组成的0和1的序列便是该节点对应字符的编码

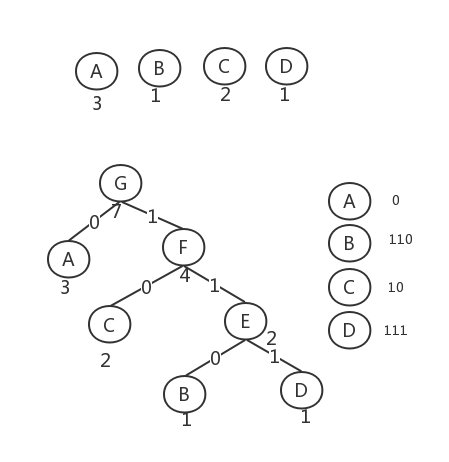
源码：

亲测有效

//哈夫曼树及哈夫曼编码 

#include<stdio.h>
#include<malloc.h>
#define MAXLEN 100 

typedef struct node{
    int weight;                                        //整型权值变量 
    int lchild,rchild,parent;                          //左孩子，右孩子，双亲 
}HFNode;

typedef HFNode HFMT[MAXLEN];
int n;

int InitHFMT(HFMT T)                                  //初始化 
{
    int i;
    printf("\n\t\t请输入共有多少个权值(小于100)：");   //叶子节点数 
    scanf("%d",&n);
    for(i = 0;i < 2*n-1;i++)
    {
        T[i].weight = 0;
        T[i].lchild = -1;
        T[i].rchild = -1;
        T[i].parent = -1;
    } 
    
    return 0;
}

int InputWeight(HFMT T)                               //输入权值 
{
    int w,i;
    for(i = 0;i < n;i++)
    {
        printf("\n\t\t请输入第%d个叶子节点的权值:",i+1);
        scanf("%d",&w);
        T[i].weight = w;
    }
    
    return 0;
}

int SelectMin(HFMT T,int i,int *p1,int *p2)           //选择两个节点中小的节点 
{
    long min1 = 999999;                              //预设两个值，使它大于可能出现的最大权值
    long min2 = 999999;
    int j;
    for(j = 0;j <= i;j++)
    {
        if(T[j].parent == -1)
        {
            if(T[j].weight < min1)
            {
                min1 = T[j].weight;                  //找出最小的权值，通过*p1带回权值 
                *p1 = j;
            }
        }
     } 
    for(j = 0;j <=i;j++)
    {
        if(T[j].parent == -1)
        {
            if(T[j].weight < min2 && j != (*p1))
            {
                min2 = T[j].weight;                 //找出次最小的权值，通过*p2带回序号 
                *p2 = j;
            }
        }
    }
    
    return 0;
}

int CreatHFMT(HFMT T)                                 //构建哈夫曼树，T(2*n-1)为根节点 
{
    int i,p1,p2;
    InitHFMT(T);
    InputWeight(T);
    for(i = n;i < 2*n-1;i++)
    {
        SelectMin(T,i-1,&p1,&p2);
        T[p1].parent = T[p2].parent = i;
        T[i].lchild = p1;
        T[i].rchild = p2;
        T[i].weight = T[p1].weight + T[p2].weight;
    }
    
    return 0;
}

int PrintHFMT(HFMT T)                                //输出向量状态表 ，打印哈夫曼树 
{
    printf("\n\t\t哈夫曼树的各边显示：");
    int i=0,k=0;
    for(i = 0;i < 2*n-1;i++)
    {
        if(T[i].lchild != -1)
        {
            if( !(k%2) )
                printf("\n");
            printf("\t\t(%d,%d),(%d,%d)",T[i].weight,T[ T[i].lchild ].weight,T[i].weight,T[ T[i].rchild ].weight);
            k++;
        }
        printf("\n\n");
     } 
    
    return 0;
}

int hfnode(HFMT T,int i) 
{
    int j; 
    j = T[i].parent; 
    if(j != -1)
    {
        if(T[j].lchild == i)
            printf("0");
        else 
            printf("1");
        i = j;
        hfnode(T,i);
    }
    
    return 0;
}

int huffmannode(HFMT T)                              //求哈夫曼编码 
{
    printf("\t\t输入的权值对应的逆置的哈夫曼编码(从叶节点到根节点):");
    int i,a,k = 0;
    for(i = 0;i < n;i++)
    {
        a = i;
        if(!(k%2))
            printf("\n");
        printf("\t\t%d:",T[i].weight);
        k++;
        hfnode(T,i);
        i = a;
    }
     
    return 0;
}

int main()
{
    HFMT HT;
    
    CreatHFMT(HT);
    PrintHFMT(HT);
    huffmannode(HT);
    printf("\n");
    
    return 0;
}