第9章 过拟合

模型的表达能力：表达能力，也称之为模型的容量(Capacity) 。

• 表达能力偏弱：比如单层线性层， 它只能学习到线性模型，无法良好地逼近非线性模型；
• 但模型的表达能力过强时， 他就有可能把训练集的噪声模态也学到，导致在测试机上面表现不佳的现象（泛化能力偏弱）。

9.1 模型的容量

模型的容量或表达能力，是指模型拟合复杂函数的能力。 一种体现模型容
量的指标为模型的假设空间(Hypothesis Space)大小，即模型可以表示的函数集的大小。

• 假设空间越大越完备， 从假设空间中搜索出逼近真实模型的函数也就越有可能；
• 如果假设空间非常受限，就很难从中找到逼近真实模型的函数。

过大的假设空间会增加搜索难度和计算代价， 在有限的计算资源的约束下，较大的假设空间并不一定能搜索出更好的函数模型。

由于观测误差的存在， 较大的假设空间中可能包含了大量表达能力过强的函数， 能够将训练样本的观测误差也学习进来，从而伤害了模型的泛化能力。

9.2 过拟合和欠拟合

• 过拟合(Overfitting)：当模型的容量过大时，网络模型除了学习到训练集数据的模态之外，还把额外的观测误差也学习进来，导致学习的模型在训练集上面表现较好，但是在未见的样本上表现不佳，也就是泛化能力偏弱，我们把这种现象叫做过拟合。
• 欠拟合(Underfitting) ：当模型的容量过小时，模型不能够很好的学习到训练集数据的模态，导致训练集上表现不佳，同时在未见的样本上表现也不佳，我们把这种现象叫做欠拟合。

9.2.1欠拟合

当我们发现当前的模型在训练集上面误差一直维持较高的状态，很难优化减少，同时在测试集上也表现不佳时，我们可以考虑是否出现了欠拟合的现象。

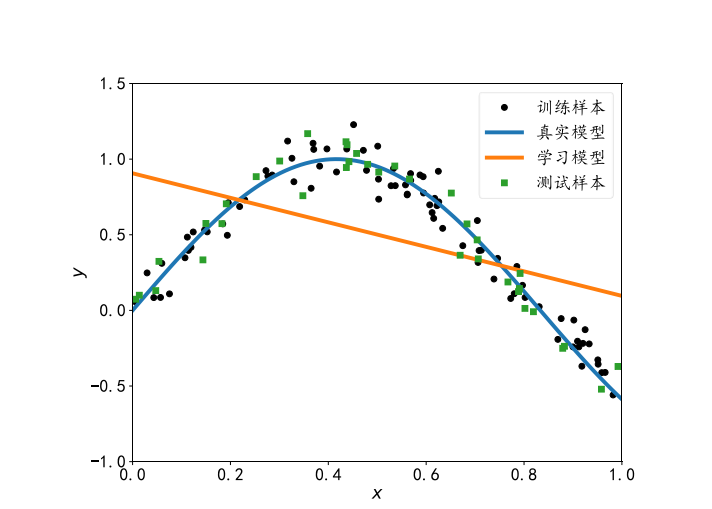
解决方法：可以通过增加神经网络的层数、增大中间维度的大小等手段， 比较好的解决欠拟合的问题。

由于现代深度神经网络模型可以很轻易达到较深的层数，我们用来学习的模型的容量一般来说是足够的，在实际使用过程中，更多的是出现过拟合现象 。

9.2.2 过拟合

学习模型在训练样本上的误差非常小， 甚至比真实模型在训练集上的误差还要小。 但是对于测试样本，模型性能急剧下降，泛化能力非常差。

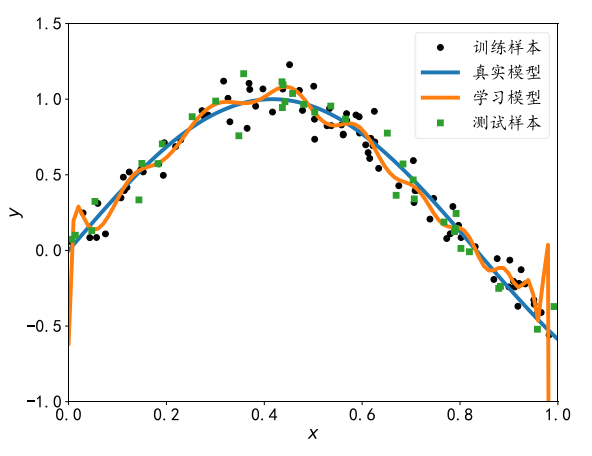
现代深度神经网络中过拟合现象非常容易出现，主要是因为神经网络的表达能力非常强，很容易就出现了神经网络的容量偏大的现象。

下面的是一系列检测并抑制过拟合现象。

9.3数据集划分

为了挑选模型超参数和检测过拟合现象，一般需要将原来的训练集再次切分为新的训练集和验证集，即数据集需要切分为训练集、验证集和测试集 3 个子集。

9.3.1验证集与超参数

由于测试集的性能不能作为模型训练的反馈， 而我们需要在模型训练时能够挑选出较合适的模型超参数，判断模型是否过拟合等，因此需要将孙联机再次切分为训练集和验证集。

划分过的训练集与原来的训练集的功能一致，用于训练模型的参数。

验证集则用于选择模型的超参数(称为模型选择， Model selection)，它的功能包括：

• 根据验证集的性能表现来调整学习率，权值衰减系数，训练次数等
• 根据验证集的性能表现来重新调整网络拓扑结构
• 根据验证集的性能表现判断是否过拟合和欠拟合

验证集与测试集的区别 ：

• 算法设计人员可以根据验证集的表现来调整模型的各种超参数的设置，提升模型的泛化能力
• 测试集的表现却不能用来反馈模型的调整，否则测试集将和验证集的功能重合， 因此在测试集上面的性能表现将无法代表模型的泛化能
  力 。

9.3.2 提前停止

• Step:对训练集中的一个 Batch 运算更新一次叫做一个 Step
• Epoch:对训练集的所有样本循环迭代一次叫做一个 Epoch。

验证集可以在数次Step或数次Epoch后使用。一般建议几个Epoch后进行一次验证运算。

通过观测训练准确率和验证准确率可以大致推断模型是否过拟合和欠拟合。

过拟合：如果模型的训练误差较低，训练准确率较高，但是验证误差较高，验证准确率较低，那么可能出现了过拟合现象。

解决方法：当观测到过拟合现象时，可以重新设计网络模型的容量，如降低网络的层数、降低网络的参数量、添加假设空间的约束等，使得模型的容量降低，从而减轻或去除过拟合现象 。

欠拟合：如果训练集和验证集上面的误差都较高，准确率较低，那么可能出现了欠拟合现象 。

解决方法：当观测到欠拟合现象时，可以尝试增大网络的容量，如加深网络的层数、 增加网络的参数量，尝试更复杂的网络结构。

由于网络的实际容量可以随着训练的进行发生改变，因此在相同的网络设定下，随着训练的进行， 可能观测到不同的过拟合/欠拟合状况。这意味着，对于神经网络，即使网络结构超参数保持不变(即网络最大容量固定)，模型依然会出现过拟合的现象，神经网络的有效容量可以很大，也可以通过稀疏化参数、 添加正则化等手段降低。

如何选择合适的 epoch 就停止训练(Early Stopping)，避免出现过拟合现象呢？

我们可以通过观察验证指标的变化，来预测最适合的 epoch 可能的位置。当发现验证准确率连
续 P 个 Epoch 没有下降时，可以预测已经达到了最适合的 epoch 附近，从而提前终止训练。

采用提前停止的模型训练算法伪代码：

9.5正则化

通过设计不同层数、大小的网络模型可以为优化算法提供初始的函数假设空间，但是模型的实际容量可以随着网络参数的优化更新而产生变化。

通过限制网络参数的稀疏性， 可以来约束网络的实际容量 。这种约束一般通过在损失函数上添加额外的参数稀疏性惩罚项实现。

这种约束一般通过在损失函数上添加额外的参数稀疏性惩罚项实现 ，为加约束之前的优化目标是：

\[MinimizeL(f_θ(x),y),(x,y)∈𝔻^{train} \]

对模型的参数添加额外的约束后，优化的目标变为 :

\[MinimizeL(f_θ(x),y)+ \lambda * \Omega(\theta),(x,y)∈𝔻^{train} \]

\(\lambda * \Omega(\theta)\)表示对网络参数𝜃的稀疏性约束函数 。一般地，参数θ的稀疏性约束通过约束参数θ的𝐿范数实现

\[𝛺(𝜃) = \sum_{\theta_i}‖𝜃_𝑖‖_𝑙 \]

新的优化目标除了要最小化原来的损失函数ℒ( x, 𝑦)之外，还需要约束网络参数的稀疏性，优化算法会在降低L(x,y)的同时，尽可能地破事网络参数\(\theta_i\)变得稀疏，他们之间的权重关系通过超参数\(\lambda\) 来平衡：

• 较大的𝜆意味着网络的稀疏性更重要
• 较小的𝜆则意味着网络的训练误差更重要
• 常用的正则化方式有L0,L1,L2正则化

9.5.1 L0正则化

L0 正则化是指采用 L0 范数作为稀疏性惩罚项𝛺(𝜃)的正则化方式：

\[𝛺(𝜃) = \sum_{\theta_i}‖𝜃_𝑖‖_0 \]

L0 范数\(‖𝜃_𝑖‖_0\)定义为\(𝜃_𝑖\)中非零元素的个数,\(‖𝜃_𝑖‖_0\)并不可导，不能利用梯度下降算法进行优化，在神经网络中使用的并不多。

9.5.2 L1正则化

采用 L1 范数作为稀疏性惩罚项𝛺(𝜃)的正则化方式叫做 L1 正则化：

\[𝛺(𝜃) = \sum_{\theta_i}‖𝜃_𝑖‖_1 \]

其中 L1 范数\(‖𝜃_𝑖‖_1\)定义为张量\(𝜃_𝑖\)中所有元素的绝对值之和。L1 正则化也叫Lasso Regularization ，它是连续可导的，在神经网络中使用广泛。

w1 = tf.random.normal([4, 3])
w2 = tf.random.normal([4, 2])
# 计算L1正则化
loss_reg = tf.reduce_sum(tf.math.abs(w1))+tf.reduce_sum(tf.math.abs(w2))

9.5.3 L2正则化

采用 L2范数作为稀疏性惩罚项𝛺(𝜃)的正则化方式叫做 L2 正则化：

\[𝛺(𝜃) = \sum_{\theta_i}‖𝜃_𝑖‖_2 \]

L2 范数\(‖𝜃_𝑖‖_2\)定义为张量\(𝜃𝑖\)中所有元素的平方和。L2正则化也叫Ridge Regularization ，它是连续可导的，在神经网络中使用广泛。

9.5.4 正则化效果

实际训练时，一般先尝试较小的正则化系数𝜆，观测网络是否出现过拟
合现象。 然后尝试逐渐增大 𝜆 参数来增加网络参数稀疏性，提高泛化能力。但是，过大的 𝜆 参数有可能导致网络不收敛，需要根据实际任务调节。

9.6 Dropout

Dropput通过随机断开神经网络的连接，减少每次训练时实际参与计算的模型的参数量；但是在测试时，Dropout会恢复所有的连接，保证模型测试获得最好的性能。

图(a)是标准的全连接神经网络， 当前节点与前一层的所有输入节点相连。在添加了 Dropout 功能的网络层中，如图(b)所示，每条连接是否断开符合某种预设的概率分布。

在 TensorFlow 中 ，可以通过tf.nn.dropout(x,rate)函数实现某条连接的Dropout功能，其中rate参数设置断开的概率值p:

# 添加dropout操作
x = tf.nn.dropout(x, rate=0.5)

也可以将 Dropout 作为一个网络层使用， 在网络中间插入一个 Dropout 层：

model.add(layers.Dropout(rate=0.5))

9.7 数据增强

除了上述介绍的方式可以有效检测和抑制过拟合现象之外，增加数据集大小是解决过拟合最重要的途径。

在有限的数据集上，通过数据增强技术可以增加训练的样本数量， 获得一定程度上的性能提升。

数据增强(Data Augmentation)是指在维持样本标签不变的条件下，根据先验知识改变样本的特征， 使得新产生的样本也符合或者近似符合数据的真实分布。

图片数据增强：TensorFlow中提供了常用图片的处理函数， 位于tf.image 子模块中。通过tf.image.resize 函数可以实现图片的缩放功能，将数据增强一般实现在预处理函数preprocess中，将 图片从文件系统读取进来后，即可进行图片数据增强操作 ：

def preprocess(x, y):
    #x：图片的路径， y：图片的数字编码
    x = tf.io.read_file(x)
    x = tf.image.decode_jpeg(x, channels=3) # RGBA
    # 图片缩放到224×224大小，这个大小根据网络设定自行调整
    x = tf.image.resize(x, [224, 224])

9.7.1 旋转

旋转图片是非常常见的图片数据增强方式，通过将原图进行一定角度的旋转运算，可以获得不同角度的新图片，这些图片的标签信息维持不变。

通过tf.image.rot90(x, k=1)可以实现图片按逆时针方式旋转k个90度：

# 图片逆时针旋转180度
x = tf.image.rot90(x, 2)

9.7.2 翻转

图片的翻转分为沿水平轴翻转和竖直轴翻转，可以通过tf.image.random_filp_left_right和tf.image.random_filp_up_down 实现图片在水平方向和竖直方向的随机翻转操作 :

# 随机水平翻转
x = tf.iamge.random_filp_left_right(x)
# 随机竖直翻转
x = tf.image.random_filp_up_down(x)

9.7.3 裁剪

通过在原图的左右或者上下方向去掉部分边缘像素，可以保持图片主体不变，同时获得新的图片样本。

在实际裁剪时，一般先将图片缩放到略大于网络输入尺寸的大小， 再进行裁剪到合适大小。

例如：网络的输入大小为224×224，那么先通过resize函数将图片缩放到224×224大小，再随机裁剪到224×224大小。

# 图片先缩放到稍大尺寸
x = tf.image.resize(x, [224, 224])
# 再随机裁剪到合适尺寸
x = tf.image.random_crop(x, [])

9.7.4 生成数据

通过生成模型在原有数据上学习到数据的分布，从而生成新的样本在一定程度上提升网络性能。如：通过条件生成对抗网络(CGAN)可以生成带标签的样本数据 。

9.7.5 其他方式

可以根据先验知识，在不改变图片标签信息的条件下，任意变换图片数据，获得新的图片。如：添加高斯噪声、变换视角、随机擦除等。

​