第6章 神经网络

6.2 全连接层

6.2.2 层方式实现

TensorFlow 中有更加高层、使用更方便的层实现方式 ：layers.Dense(units,activation)

• 输出节点数：Units
• 激活函数类型：activation

根据输入、输出节点数自动创建并初始化权值矩阵 W 和偏置向量 b。

x = tf.random.normal([4, 28 * 28])
fc = layers.Dense(512, activation=tf.nn.relu)
h1 = fc(x)

可以通过类内部的成员名kernel 和 bias 来获取权值矩阵 W 和偏置 b：

print(fc.kernel)  # 获取 Dense 类的权值矩阵
print(fc.bias)  # 获取 Dense 类的偏置向量

在优化参数时，需要获得网络的所有待优化的参数张量列表，可以通过类的trainable_variables 来返回待优化参数列表：

print(fc.trainable_variables)

网络层除了保存了待优化张量 trainable_variables，还有部分层包含了不参与梯度优化的张量，可以通过 non_trainable_variables 成员返回所有不需要优化的参数列表。

如果希望获得所有参数列表， 可以通过类的 variables 返回所有内部张量列表：

print(fc.variables)

利用网络层类对象进行前向计算时，只需要调用类的__call__方法即可写成 fc(x)方式，它会自动调用类的__call__方法，在__call__方法中自动调用 call 方法 。

6.3 神经网络

在设计全连接网络时，网络的结构配置等超参数可以按着经验法则自由设置，只需要遵循少量的约束即可。

6.3.1张量方式实现

定义各层w、b:

# 隐藏层1张量
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 隐藏层2张量
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
# 隐藏层3张量
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
b3 = tf.Variable(tf.zeros([64]))
# 输出层张量
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]))

在使用 TensorFlow 自动求导功能计算梯度时，需要将前向计算过程放置在tf.GradientTape()环境中

with tf.GradientTape() as tape:
    # 隐藏层 1 前向计算， [b, 28*28] => [b, 256]
    h1 = x @ w1 + tf.broadcast_to(b1, (x.shape[0], 256))
    h1 = tf.nn.relu(h1)

    # 隐藏层 2 前向计算， [b, 256] => [b, 128]
    h2 = h1 @ w2 + b2
    h2 = tf.nn.relu(h2)
    
    # 隐藏层 3 前向计算， [b, 128] => [b, 64]
    h3 = h2 @ w3 + b3
    h3 = tf.nn.relu(h3)

    # 输出层计算
    h4 = h3 @ w4 + b4

6.3.2 层方式实现

对于这种数据依次向前传播的网络， 也可以通过 Sequential 容器封装成一个网络大类对象，调用大类的前向计算函数即可完成所有层的前向计算 ：

# 通过Sequential容器封装为一个网络类
model = keras.models.Sequential([
    layers.Dense(256, activation=tf.nn.relu),
    layers.Dense(128, activation=tf.nn.relu),
    layers.Dense(64, activation=tf.nn.relu),
    layers.Dense(10, activation=None)
])
# 前向计算时只需要调用一次网络大类对象即可完成所有层的按序计算：
out = model(x)
print(out)

6.3.3 优化目标

前向传播：把神经网络从输入到输出的计算过程叫做前向传播

前向传播的最后一步就是完成误差的计算。

我们希望通过在训练集𝔻𝑡𝑟𝑎𝑖𝑛上面学习到一组参数𝜃使得误差的误差θ最小。

利用误差反向传播算法进行反向计算的过程也叫反向传播。

计算全连接层的参数量： 输入特征长度为\(d_(in)\) 输入特征长度为 \(d_(out)\)的网络层 ,再加上偏置 b 的参数:总参数量为\(d_(in)*d_(out)+d_(out)\)

6.4 激活函数

6.4.1 Sigmoid

Sigmoid 函数也叫Logistic函数，定义为

\[Sigmoid := \frac {1}{1+e^{-x}} \]

它的一个优良特性就是能够把𝑥 ∈ 𝑅的输入“压缩” 到𝑥 ∈ [0,1]区间， 这个区间的数值在机器学习常用来表示以下意义:

• 概率分布 [0,1]区间的输出和概率的分布范围契合，可以通过 Sigmoid 函数将输出转译为概率输出。
• 信号强度 一般可以将 0~1 理解为某种信号的强度

Sigmoid 函数连续可导， 相对于阶跃函数，可以直接利用梯度下降算法优化网络参数，应用的非常广泛 。

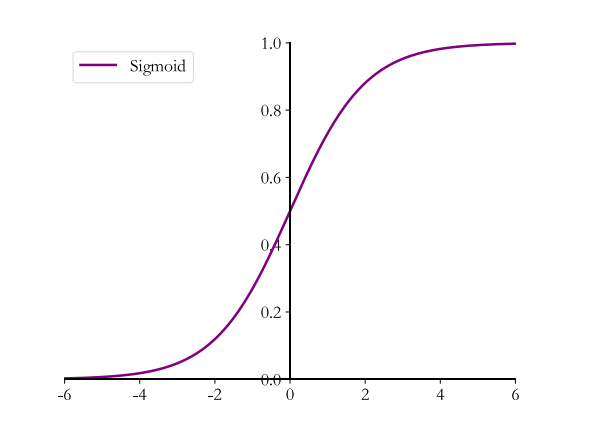
可以通过tf.nn.sigmoid实现 Sigmoid 函数：

# 构造-6~6的输入向量
x = tf.linspace(-6., 6., 10)
print(x)
y = tf.nn.sigmoid(x)
print(y)

6.4.2 ReLU(修正线性单元)

Sigmoid 函数在输入值较大或较小时容易出现梯度值接近于 0 的现象，称为梯度弥散现象，网络参数长时间得不到更新，很难训练较深层次的网络模型。

ReLU 函数定义 ：

\[ReLU(x) :=max(0, x) \]

ReLU对于小于0的值全部抑制为0；对于正数则直接输出

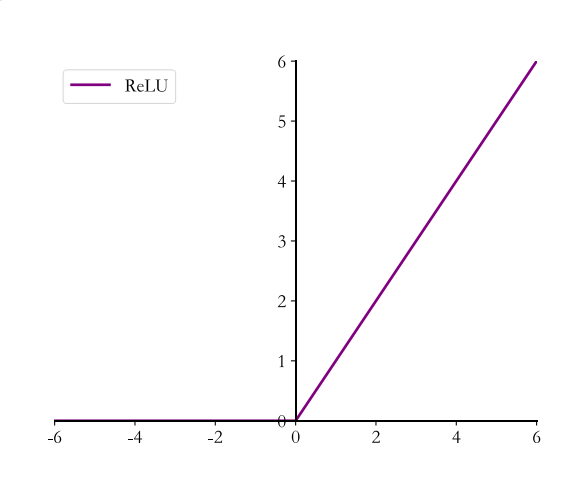
在 TensorFlow 中，可以通过 tf.nn.relu 实现 ReLU 函数：

# 构造-6~6的输入向量
x = tf.linspace(-6., 6., 10)
print(x)
y = tf.nn.relu(x)
print(y)

除了可以使用函数式接口 tf.nn.relu 实现 ReLU 函数外，还可以像 Dense 层一样将ReLU 函数作为一个网络层添加到网络中，对应的类为 layers.ReLU()类,不计入网络的层数。

6.4.3 LeakyReLU

ReLU 函数在𝑥 < 0时梯度值恒为 0，也可能会造成梯度弥散现象。

LeakyReLU函数解决了这一点，表达式为：

\[LeakyReLU = \begin{cases} x, & \text{x≥0 }\\ p*x,& \text{x<0} \end{cases} \]

• 𝑝为用户自行设置的某较小数值的超参数
• 𝑝 = 0时， LeayReLU 函数退化为 ReLU 函数
• 当𝑝 ≠ 0时， 𝑥 < 0能够获得较小的梯度值𝑝

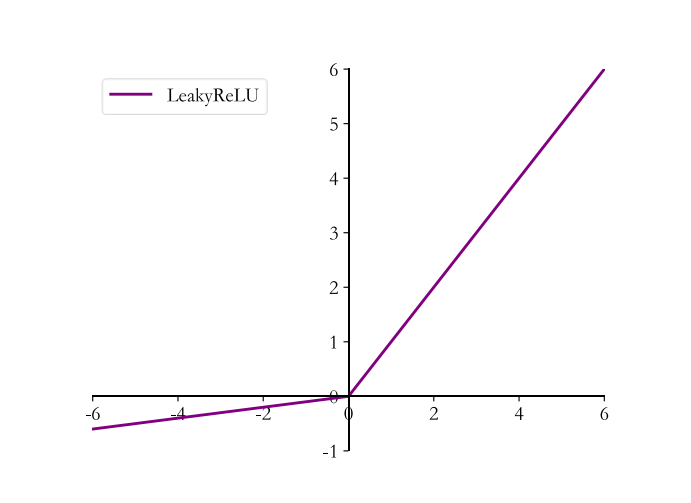
在 TensorFlow 中，可以通过 tf.nn.leaky_relu 实现 LeakyReLU 函数

y = tf.nn.leaky_relu(x, alpha=0.1)
print(y)

• alpha 参数即𝑝参数
• tf.nn.leaky_relu 对应的类为 layers.LeakyReLU，可以通过LeakyReLU(alpha)创建 LeakyReLU 网络层，并设置𝑝参数，像 Dense 层一样将 LeakyReLU层放置在网络的合适位置 。

6.4.4 Tanh

Tanh 函数能够将𝑥 ∈ 𝑅的输入“压缩” 到[-1,1]区间，定义为：

\[tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} = 2 * sigmoid(2x) - 1 \]

tanh 激活函数可通过 Sigmoid 函数缩放平移后实现 :

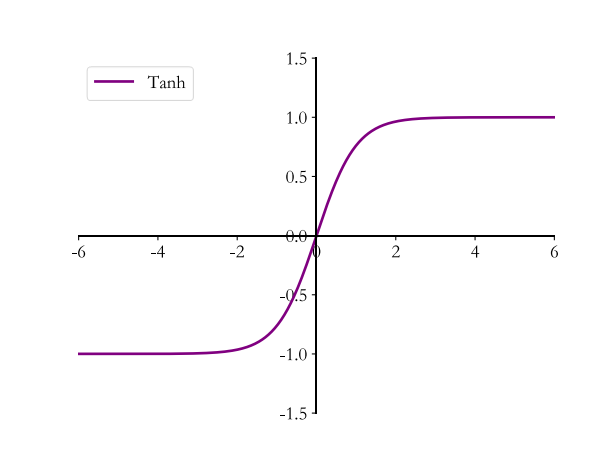
在 TensorFlow 中，可以通过 tf.nn.tanh 实现 tanh 函数：

y = tf.nn.tanh(x)
print(y)

6.5 输出层设计

输出层除了和所有的隐藏层一样，完成维度变换、特征提取的功能，还作为输出层使用， 需要根据具体的任务场景来决定是否使用激活
函数，以及使用什么类型的激活函数 。

常见的输出类型包括：

• 输出为整个实数空间，或者某段普通的实数空间，比如函数值趋势的预测 ， 年龄的预测问题等
• 输出值特别地落在[0, 1]的区间，如图片生成，像素值一般用[0,1]表示，或者二分类的问题等
• 输出值落在[0, 1]的区间， 并且所有输出值之和为 1，常见的多分类问题。
• 输出值在[-1, 1]之间

6.5.1 普通实数空间

输出层可以不加激活函数

6.5.2 [0, 1]区间

需要在输出层后添加某个合适的激活函数𝜎，其中 Sigmoid 函数刚好具有此功能 。

6.5.3 [0,1]区间，和为1

以多分类问题最为常见 ，可以通过在输出层添加 Softmax 函数实现，Softmax 函数不仅可以将输出值映射到[0,1]区间，还满足所有的输出值之和为 1 的特性。

在 TensorFlow 中，可以通过 tf.nn.softmax 实现 Softmax 函数：

z = tf.constant([2., 1., 0.1])
y = tf.nn.softmax(z)
print(y)

在 Softmax 函数的数值计算过程中，容易因输入值偏大发生数值溢出现象; 在计算交叉熵时，也会出现数值溢出的问题。

为了数值计算的稳定性 TensorFlow 中提供了一个统一的接口，将 Softmax 与交叉熵损失函数同时实现，同时也处理了数值不稳定的异常，一般推荐使用，避免单独使用 Softmax 函数与交叉熵损失函数。

接口为：tf.keras.losses.categorical_crossentopy(y_true, y_pred, form_logits=False)

• y_true代表了one-hot 编码后的真实标签
• y_pred 表示网络的预测值
• from_logits :
  • from_logits为True时，y_pred表示须为未经过Softmax函数的变量z；
  • from_logits为False时,y_pred表示为经过 Softmax 函数的输出

z = tf.random.normal([2, 10]) # 构造输出层的输出
y_onehot = tf.constant([1, 3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10) # one-hot 编码
loss = keras.losses.categorical_crossentropy(y_onehot, z, from_logits=True)
loss = tf.reduce_mean(loss)# 计算平均交叉熵损失
print(loss)

6.5.4 [-1, 1]

如果希望输出值的范围分布在[-1, 1]，可以简单地使用 tanh 激活函数 ：

x = tf.linspace(-6., 6., 10)
y = tf.tanh(x)
print(y)

6.6 误差计算

常见的误差计算函数有：均方差、 交叉熵、 KL 散度、 Hinge Loss 函数等

均方差函数和交叉熵函数在深度学习中比较常见

均方差主要用于回归问题

交叉熵主要用于分类问题。

6.6.1均方差

均方差（MSE）函数把输出向量和真实向量映射到笛卡尔坐标系的两个点上，通过计算这两个点之间的欧式距离(准确地说是欧式距离的平方)来衡量两个向量之间的差距：

​

\[MSE := \frac{1}{d_{out}}\sum_{i=1}^{d_{out}}(y_i-o_i)^2 \]

MSE 误差函数的值总是大于等于 0，当 MSE 函数达到最小值 0 时， 输出等于真实标签，此时神经网络的参数达到最优状态。

在 TensorFlow中， 可以通过函数方式或层方式实现 MSE 误差计算：

o = tf.random.normal([2, 10])  # 构造网络输出
y_onehot = tf.constant([1, 3])  # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10)
loss = keras.losses.MSE(y_onehot, o)  # 计算均方差
print(loss)
# TensorFlow MSE 函数返回的是每个样本的均方差，需要在样本数量上再次平均来获得batch 的均方差：
loss = tf.reduce_mean(loss)  # 计算batch均方差
print(loss)

也可以通过层方式实现，对应的类为 keras.losses.MeanSquaredError()：

criteon = keras.losses.MeanSquaredError()
loss = criteon(y_onehot, o)  # 计算batch均方差
print(loss)

6.6.2 交叉熵

熵越大，代表不确定性越大，信息量也就越大 。

交叉熵的定义：

\[H(p,q) := -\sum_{i=0}p(i)log_2q(i) \]

通过变换， 交叉熵可以分解为 p 的熵𝐻(𝑝)与 p,q 的 KL 散度(Kullback-Leibler Divergence)的和:

\[𝐻(𝑝, 𝑞) = H(p) + D_{KL}(p|q) \]

KL 定义为 :

\[D_{KL}(p|q) = \sum_{x\epsilon X}p(x)log(\frac{p(x)}{q(x)}) \]

KL 散度是 Solomon Kullback 和 Richard A. Leibler 在 1951 年提出的用于衡量 2 个分布之间距离的指标， 𝑝 = 𝑞时， 𝐷𝐾𝐿(𝑝|𝑞)取得最小值 0 .

• 交叉熵和 KL 散度都不是对称的：

\[𝐻(𝑝, 𝑞) ≠ H(q,p)\\ D_{KL}(p|q)≠D_{KL}(q|p) \]

交叉熵可以很好地衡量 2 个分布之间的差别.

6.7 神经网络类型

6.7.1卷积神经网络

这其中比较流行的模型有用于图片分类的 AlexNet， VGG， GoogLeNet， ResNet， DenseNet 等，用于目标识别的 RCNN， FastRCNN， Faster RCNN， Mask RCNN 等。

6.7.2 循环神经网络

卷积神经网络由于缺乏 Memory 机制和处理不定长序列信号的能
力，并不擅长自然语言处理任务。 循环神经网络 （RNN）被证明非常擅长处理序列信号。 LSTM 网络，作为RNN的变种，它较好地克服了RNN 缺乏长期记忆、 不擅长处理长序列的问题，在自然语言处理中得到了广泛的应用。

基于 LSTM 模型， Google 提出了用于机器翻译的 Seq2Seq 模型，并成功商用于谷歌神经机器翻译系统(GNMT)。其他的 RNN 变种还有 GRU，双向 RNN 等 。

6.7.3 注意力（机制）网络

RNN 并不是自然语言处理的最终解决方案，近年来随着注意力机制(Attention)的提出，克服了 RNN 训练不稳定、 难以并行化等缺陷，在自然语言处理和图片生成等领域中逐渐崭露头角。

2017 年， Google 提出了第一个利用纯注意力机制实现的网络模型 Transformer，随后基于Transformer 相继提出了一系列的用于机器翻译的注意力网络模型，如 GPT， BERT， GPT-2等。

基于注意力机制，尤其是自注意力(Self-attention)机制构建的网络也取得了不错的效果，比如基于自注意力机制的 BigGAN 模型等 。

6.7.4 图神经网络

图片、 文本等数据具有规则的空间、时间结构，称之为 Euclidean Data。

图卷积网络(Graph Convolution Network， GCN)模型。 GCN 算法实现简单，从空间一阶邻居信息聚合的角度也能直观理解，在半监督任务上取得了不错效果。随后，一系列的网络模型相继被提出，如 GAT， EdgeConv， DeepGCN 等 。

对于回归问题，除了 MSE 均方差可以用来测试模型的性能，还可以用平均绝对误差(Mean Absolute Error, MAE)来衡量模型的性能 。