【做题笔记】洛谷P8518 [IOI2021] 分糖果
Problem
题目大意：
给你一个长度为 \(n\) 的序列 \(c\)，你有一个序列 \(a\)，初始时 \(a\) 的每个值都为 \(0\)。有 \(q\) 次操作，每次操作将一个区间加上一个数。每次操作后若 \(a_i<0\) 则 \(a_i \gets 0\)。若 \(a_i>c_i\) 则 \(a_i \gets c_i\)。问 \(q\) 次操作后序列 \(a\) 的值。
Solution
我们定义 \(a_i \gets 0\) 为“碰下壁”，\(a_i \gets c_i\) 为“碰上壁”。
容易发现，对于每个 \(a_i\)，最后一次碰壁前的操作是无用的。于是我们考虑对于每个点求出最后一次碰壁的时间。
假设正在考虑第 \(i\) 个点。
假设没有推平操作，那么这个数的变化情况应该是这样一条曲线：
观察发现，对于相邻的一次碰上壁和一次碰下壁：
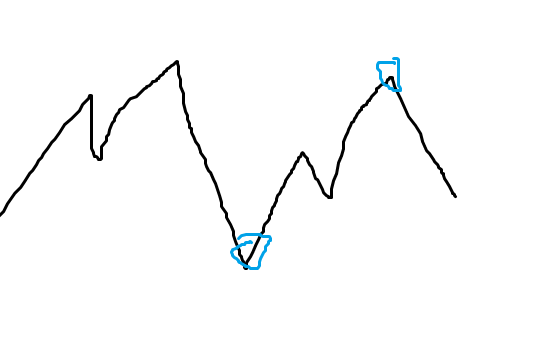
他们的差一定 \(>c_i\)。
于是考虑使用这个性质来找到最后一次碰上壁和最后一次碰下壁。
具体怎么实现呢？
我们在时间（即每次操作）上建一棵线段树，在线段树的每个节点记录这个区间的和，前缀最大最小值。则我们查询只要找最后一次碰上壁和最后一次碰下壁中靠前的那个的位置，另一个则为从这个位置开始一直道最后的另一个极值。
因为我们需要查询的是一段后缀，所以若当前在区间 \([l,r]\)，则同时还要记录 \([r+1,q]\) 这个区间的区间和，前缀最大最小值。
对于当前区间，若右半部分（\([mid+1,q]\)）的极差 \(>c_i\)，则答案在右儿子，否则在左儿子。
找到正确的位置后，考虑维护答案，可以把碰壁操作看成整体位移。以碰上壁为例，则相当于将整个曲线向下移动一段距离，也就是整体减去一个值，如图所示：
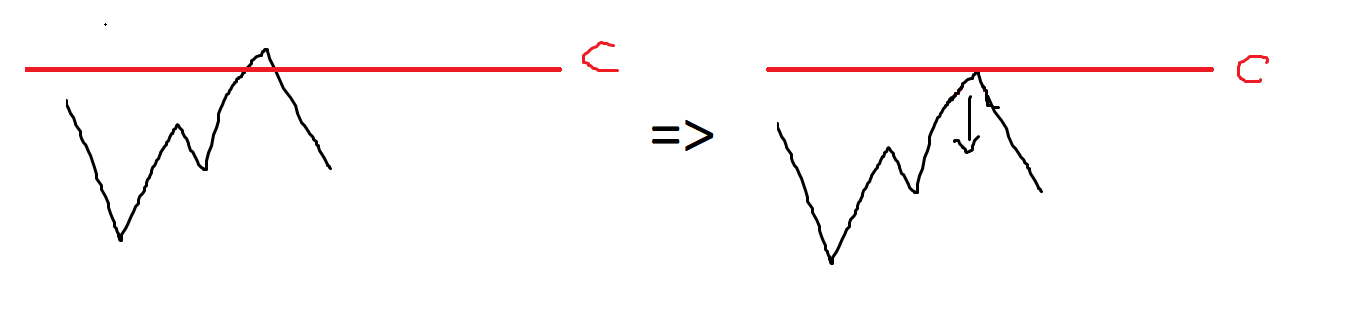
所以最终答案为整个后缀的和减去最后一次碰壁的前缀和再加上位移量。
但是上面的只是单独一个点的做法。那有 \(n\) 个点的情况呢？
可以进行差分，也就是对于一个影响范围为 \([l,r]\) 的操作，在点 \(l\) 时将其插入线段树，在点 \(r+1\) 时将其从线段树中删除即可。
Code
//Think twice,code once.
#include<vector>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,q;
vector<int>c,lt,rt,vv,ans;
vector<pair<int,int> >v[200005];
struct Segment_Tree
{
long long sum[800005],mx[800005],mn[800005];//sum，mx，mn 分别为区间和，最大最小值。
int l[800005],r[800005];
void build(int ll,int rr,int k)
{
l[k]=ll;r[k]=rr;
if(ll==rr) return ;
int mid=(l[k]+r[k])/2;
build(ll,mid,k*2);
build(mid+1,rr,k*2+1);
return ;
}
void update(int p,int val,int k)
{
if(l[k]==r[k])
{
sum[k]+=val;
mx[k]=max(0ll,sum[k]);
mn[k]=min(0ll,sum[k]);
return ;
}
int mid=(l[k]+r[k])/2;
if(p<=mid) update(p,val,k*2);
else update(p,val,k*2+1);
sum[k]=sum[k*2]+sum[k*2+1];
mx[k]=max(mx[k*2],sum[k*2]+mx[k*2+1]);
mn[k]=min(mn[k*2],sum[k*2]+mn[k*2+1]);
return ;
}
long long query(int cc,long long rsum,long long rmx,long long rmn,int k)//这里 rsum,rmx,rmn 分别代表当前区间 [l,r] 的后缀 [r+1,q] 的和，最大最小值。
{
if(l[k]==r[k])
{//二分得到的位置一定是最后一次碰上壁和最后一次碰下壁中的某一个，所以可以根据 sum 的值来判断他是碰上壁还是碰下壁，进而判断最后一次碰壁时碰上壁还是碰下壁
if(sum[k]<=0)
{
if(rmx>cc) return cc+rsum-rmx;
else return rsum-rmn;
}
else
{
if(rmn<-cc) return rsum-rmn;
else return cc+rsum-rmx;
}
}
long long nsum=rsum+sum[k*2+1];
long long nmx=max(mx[k*2+1],sum[k*2+1]+rmx);
long long nmn=min(mn[k*2+1],sum[k*2+1]+rmn);
//将 [mid+1,r] 与后缀合并。
if(nmx-nmn<=cc) return query(cc,nsum,nmx,nmn,k*2);
else return query(cc,rsum,rmx,rmn,k*2+1);
}
}tr;
vector<int>distribute_candies(vector<int>c,vector<int>lt,vector<int>rt,vector<int>vv)
{
n=c.size();
q=vv.size();
tr.build(0,q,1);
c.push_back(0);
lt.push_back(0);
rt.push_back(0);
vv.push_back(0);
for(int i=n-1;i>=0;i--) swap(c[i],c[i+1]);
for(int i=q-1;i>=0;i--) swap(lt[i],lt[i+1]);
for(int i=q-1;i>=0;i--) swap(rt[i],rt[i+1]);
for(int i=q-1;i>=0;i--) swap(vv[i],vv[i+1]);
for(int i=1;i<=q;i++)
{
lt[i]++,rt[i]++;
v[lt[i]].emplace_back(i,vv[i]);
v[rt[i]+1].emplace_back(i,-vv[i]);
}//差分
for(int i=1;i<=n;i++)
{
for(auto j:v[i])
tr.update(j.first,j.second,1);
ans.push_back(tr.query(c[i],0,0,0,1));
}
return ans;
}
