【做题笔记】CF1254C Point Ordering
感谢小笼包凸包之神 djwj223 提供的思路。
Problem
题目大意：
交互题，有一个由 \(n\) 个顶点组成的没有三点共线的凸包，每次可以有两种询问：
- 第一种询问三个点，返回这三个点组成的三角形的面积的 \(2\) 倍。
- 第二种询问三个点 \(A_i,A_j,A_k\)，返回 \(\overrightarrow{A_iA_j} \times \overrightarrow{A_iA_k}\) 的正负。
要求在 \(3n\) 次询问后从 \(1\) 开始逆时针输出点的编号。如：
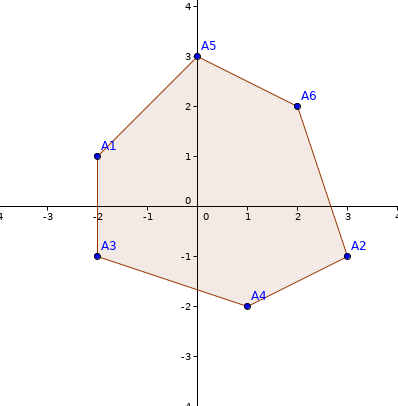
应该输出 0 1 3 4 2 6 5。
Solution
考虑第二种询问相当于询问 \(A_k\) 在 \(A_iA_j\) 的左侧（正）还是右侧（负）。
然后考虑钦定两个点，发现其他的点与这两个点的询问可以求出他们构成的三角形的高（以钦定的两个点连成的线段为底）。
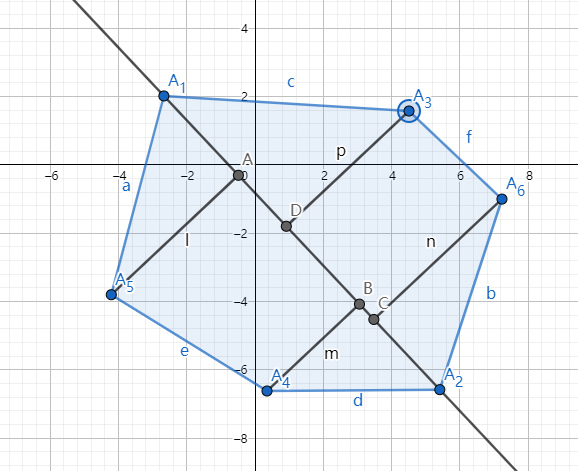
于是就有这样一个想法：
任意找两个点，然后用 \(n-2\) 次询问得到其他点在左侧还是右侧。再使用 \(n-2\) 次询问得到其他点到直线的距离的相对大小。容易发现直线切割后的两半部分都依然是凸包，所以点到直线的相对大小必定是先增大再减小。
接下来的问题就是对于每一部分确定哪些在左侧，哪些在右侧。
一个比较容易想到的做法是找到距离最大的点，然后用操作 \(2\) 区分点在左侧还是右侧。然后对于右侧从小到大排序，左侧从大到小排序。
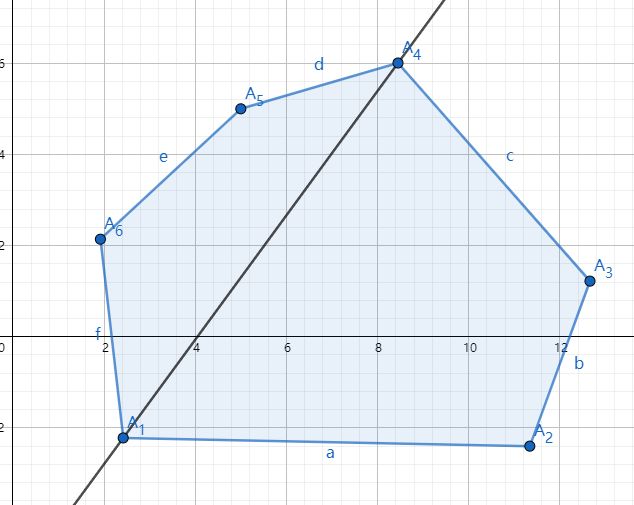
由于两部分都会取出一个顶点，再去掉最初钦定的两个点，要对其余的每个点进行询问，所以需要 \(n-4\) 次询问。
但是最高点可能有两个，不过手玩一下就会发现没什么问题。
总询问次数 \(n-2+n-2+n-4=3n-8\)，但是当最初选择的两个点相邻的时候会变成 \(n-2+n-2+n-3=3n-7\)。
还有不懂的可以看代码：
Code
//Think twice,code once.
#include<vector>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,p;
long long mx;
vector<pair<long long,int> >r,l,a1,a2;
vector<int>ans;
int main()
{//钦定最初的两个点1 2
scanf("%d",&n);
for(int i=3;i<=n;i++)
{
printf("2 1 2 %d\n",i);fflush(stdout);
int x;scanf("%d",&x);
if(x==-1) r.emplace_back(0,i);
else l.emplace_back(0,i);
}//区分左右侧
ans.push_back(1);
//先处理右侧
for(int i=0;i<(int)r.size();i++)
{
printf("1 1 2 %d\n",r[i].second);fflush(stdout);//询问点到直线的距离
scanf("%lld",&r[i].first);
if(r[i].first>mx) mx=r[i].first,p=r[i].second;//记录最高点
}
for(auto i:r)
{
if(i.second==p) continue;
printf("2 1 %d %d\n",p,i.second);fflush(stdout);//判断在最高点左侧还是右侧
int x;scanf("%d",&x);
if(x==-1) a1.push_back(i);
else a2.push_back(i);
}
sort(a1.begin(),a1.end());sort(a2.begin(),a2.end());reverse(a2.begin(),a2.end());//右侧从小到大，左侧从大到小
for(auto i:a1) ans.push_back(i.second);
if(p) ans.push_back(p);
for(auto i:a2) ans.push_back(i.second);
ans.push_back(2);
p=mx=0;a1.clear();a2.clear();
//处理左侧
for(int i=0;i<(int)l.size();i++)
{
printf("1 1 2 %d\n",l[i].second);fflush(stdout);//同上
scanf("%lld",&l[i].first);
if(l[i].first>mx) mx=l[i].first,p=l[i].second;//同上
}
for(auto i:l)
{
if(i.second==p) continue;
printf("2 1 %d %d\n",p,i.second);fflush(stdout);//同上
int x;scanf("%d",&x);
if(x==-1) a1.push_back(i);
else a2.push_back(i);
}
sort(a1.begin(),a1.end());sort(a2.begin(),a2.end());reverse(a2.begin(),a2.end());//同上
for(auto i:a1) ans.push_back(i.second);
if(p) ans.push_back(p);
for(auto i:a2) ans.push_back(i.second);
printf("0 ");
for(auto i:ans) printf("%d ",i);
puts("");
return 0;
}
