Codeforces Round #843 (Div. 2) 做题记录
Codeforces Round #843 (Div. 2) 做题记录
A1&A2. Gardener and the Capybaras
Problem
CF1775A2 Gardener and the Capybaras
题目大意：
给你一个由 a 和 b 组成的字符串，要将它分成三个子串，使得中间那个串字典序最大或最小，输出任意一种方案。若无解，输出 :(。
Solution
这个只有 a 和 b 的条件其实是无用的。
考虑使其字典序最小，则一定是中间找出一个字典序最小的字符成为中间一段，剩下的成为左右两段。故可以使中间的串字典序最小当且仅当全串最小的字符在中间（即非第一个和最后一个字符）出现。
考虑使其字典序最大，沿用上面的思路一定是从字典序最大的字符开始。但为了使其字典序更大应该一直往后扩展直到最后一个字符之前。
可以证明上面两种构造方法是不劣的，所以若无法用上面两种方法构造则无解。
Code
// Think twice, code once.
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int T;
string s;
int main() {
cin>>T;
while (T--) {
cin>>s;
char mn=127,mx=0;
for (char ch:s) mn=min(mn,ch),mx=max(mx,ch);
string s1="",s2="",s3="";
for (int i=1;i<(int)s.length()-1;i++)
if (s[i]==mn) {
for (int j=0;j<i;j++) printf("%c",s[j]);
putchar(' ');
printf("%c",s[i]);
putchar(' ');
for (int j=i+1;j<(int)s.length();j++) printf("%c",s[j]);
puts("");
goto NXT;
}
for (int i=1;i<(int)s.length()-1;i++)
if (s[i]==mx) {
for (int j=0;j<i;j++) s1.push_back(s[j]);
for (int j=i;j<(int)s.length()-1;j++) s2.push_back(s[j]);
s3.push_back(s.back());
break;
}
if (s2>=s1&&s2>=s3) cout<<s1<<' '<<s2<<' '<<s3<<'\n';
else puts(":(");
NXT:;
}
return 0;
}
B. Gardener and the Array
Problem
CF1775B Gardener and the Array
题目大意：
给你一个序列，你要判断能否找到两个不同的子序列使得他们或起来相等。但序列中数的大小为 \(2^{2 \times 10^5}\)。题目会给出每个数二进制下哪些位为 \(1\)，保证输入量不超过 \(10^5\)。
Solution
首先容易想到一个结论：若题目有解则一定存在一种方案使得其中一个子序列是全串。
可以通过调整法证明这个结论：考虑任意一个合法解 \(A,B\)，设 \(|A| \ge |B|\)，考虑所有不在 \(A\) 中的数，若将其加入 \(A\) 后或和不变则直接加入，否则其一定也不在 \(B\) 中，将其同时加入两个子序列即可。
然后容易想到另一个结论：若题目有解则一定存在一种方案使得其中一个子序列是全串且另一个子序列是全串扣掉某个数。
因为全串的或和一定大于等于任意一个子串的或和，所以当存在一个合法解使得其中一个子序列是全串的情况下，往另一个串里添数一定合法，一直添加直到只剩一个数即可。
故这题做法呼之欲出：求全串或和，枚举不在另一个子串内的数，计算是否合法。
具体实现时可以用一个数组 \(b_i\) 表示全串中二进制下第 \(i\) 位为 \(1\) 的数的个数。判断是否合法只要枚举这个数为 \(1\) 的位，判断这一位的 \(b\) 是否 \(> 1\) 即可。
Code
// Think twice, code once.
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int T,n,b[200005];
vector<int> c[100005];
int check(int x) {
int flag=1;
for (int i:c[x])
if (!--b[i]) flag=0;
for (int i:c[x]) b[i]++;
return flag;
}
int main() {
scanf("%d",&T);
while (T--) {
scanf("%d",&n);
for (int i=1;i<=n;i++) {
int len;
scanf("%d",&len);
c[i].resize(len);
for (int j=0;j<len;j++)
scanf("%d",&c[i][j]),b[c[i][j]]++;
}
for (int i=1;i<=n;i++)
if (check(i)) {
puts("Yes");
goto NXT;
}
puts("No");
NXT:;
for (int i=1;i<=n;i++) {
for (int j:c[i]) b[j]--;
vector<int> ().swap(c[i]);
}
}
return 0;
}
C. Interesting Sequence
Problem
题目大意：
给你两个数 \(n,x\)，求最小的 \(m\) 使得 \(n \And (n+1) \And (n+2) \And \ldots \And m = x\)。无解输出 -1。
Solution
手玩几个数据可以发现，一段连续的数与起来的结果一定是第一个数二进制下的一段后缀变成 \(0\) 的形式。进一步可以发现当 \(m\) 最小时只有 \(n \And (n+1) \And (n+2) \And \ldots \And m = n \And m\)。因为 \(m\) 一定是最小的将 \(n \oplus x\) 的最高位覆盖成 \(0\) 的数，显然这个数的后面几位全为 \(0\)，故结论正确。
所以本题做法是先求出 \(n \oplus x\) 的值，然后不断将 \(n\) 的后缀推平直求出 \(m\)，然后判断是否合法即可。
无解的几种情况：\(x > n\)，\(n \oplus x\) 的最高位的下一位在 \(n\) 的二进制下是 \(1\)，\(n \oplus x\) 不是 \(n\) 的一段后缀。只有第二种情况需要特殊判断，因为剩下两种直接计算 \(n \And m\) 一定 \(\neq x\)。但第二种情况直接计算得到的 \(m\) 不适用于第二个结论。一个 Hack 数据是 3 2。
Code
// Think twice, code once.
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int T;
long long n,x;
int main() {
scanf("%d",&T);
while (T--) {
scanf("%lld%lld",&n,&x);
if (n==x) {printf("%lld\n",n);continue;}
long long m=n^x;
long long ans=1;
long long nn=n;
while (ans<=m) {
if (nn&ans) nn^=ans;
ans<<=1;
}
// printf("%lld %lld\n",ans,nn);
if (n&ans) {puts("-1");continue;}
else {
nn|=ans;
if ((n&nn)==x) printf("%lld\n",nn);
else puts("-1");
}
}
return 0;
}
D. Friendly Spiders
Problem
题目大意：
给你 \(n\) 个数 \(a_i\)，若 \(\gcd(a_i, a_j) \neq 1\) 则在 \(i,j\) 之间连一条无向变，求从 \(s\) 到 \(t\) 的最短路。
Solution
这是一个经典的 Trick：对于每个因子建立一个虚点，每个点与自己的因子连边。
这样做显然是对的，但是边数到了 \(O(n \sqrt{n})\)。不过容易发现只需要考虑质因子即可，这样边数就是 \(O(n \log n)\) 了。
Code
// Think twice, code once.
#include <stack>
#include <queue>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int n,s,t,dis[600005],pre[600005];
int cnt,prime[300005],f[300005];
struct graph {
int tot,hd[600005];
int nxt[10000005],to[10000005];
void add(int u,int v) {
nxt[++tot]=hd[u];
hd[u]=tot;
to[tot]=v;
return ;
}
}g;
queue<int> q;
stack<int> ans;
int main() {
for (int i=2;i<=300000;i++)
if (!f[i]) {
prime[++cnt]=i;
for (int j=2*i;j<=300000;j+=i) f[j]=1;
}
scanf("%d",&n);
for (int i=1;i<=n;i++) {
int x;
scanf("%d",&x);
for (int j=1;j<=cnt&&prime[j]*prime[j]<=x;j++)
if (x%prime[j]==0) {
g.add(i,n+j);
g.add(n+j,i);
while (x%prime[j]==0) x/=prime[j];
}
if (x!=1) {
int pos=lower_bound(prime+1,prime+cnt+1,x)-prime;
g.add(i,n+pos);
g.add(n+pos,i);
}
}
scanf("%d%d",&s,&t);
memset(dis,-1,sizeof(dis));
q.push(s);
dis[s]=0;
while (!q.empty()) {
int now=q.front();q.pop();
for (int i=g.hd[now];i;i=g.nxt[i])
if (dis[g.to[i]]==-1) {
dis[g.to[i]]=dis[now]+1;
pre[g.to[i]]=now;
q.push(g.to[i]);
}
}
if (dis[t]==-1) {puts("-1");return 0;}
for (int now=t;now;now=pre[now])
if (now<=n) ans.push(now);
printf("%d\n",(int)ans.size());
while (!ans.empty()) printf("%d ",ans.top()),ans.pop();
puts("");
return 0;
}
E. The Human Equation
Problem
题目大意：
给你一个序列，你可以执行任意次以下操作：
选出一个子序列，将奇数位 \(+1\)，偶数位 \(-1\)，或将奇数位 \(-1\)，偶数位 \(+1\)。
问最少几次操作使得序列变成全 \(0\)。
Solution
显然正数只会 \(-1\)，负数只会 \(+1\)。
显然本题可以贪心，即对于每次操作尽量往后扩展。
从前往后考虑每一个数，两个计数器 \(z,f\) 分别表示以正数结尾和以负数结尾的操作产生的贡献。
对于当前这个数 \(x\)，若是正数：若负数产生的贡献大于当前数，则表示当前数可以被加入之前的操作一起消掉。此时这些贡献转化成了正数的贡献。故 \(z \leftarrow z + x,f \leftarrow f - x\)。
否则，说明需要额外操作，故答案加上 \(x - f\)，并且贡献也转化成了正数的贡献，故 \(z \leftarrow z + x,f \leftarrow 0\)。
对于 \(x\) 是负数的情况同理。
为什么这样做是对的？因为对于每次操作，将其贡献加在任意位置都是对的。这种做法将贡献加在了操作的第一个位置，显然正确。
Code
// Think twice, code once.
#include <stack>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int T,n,a[200005];
long long ans;
int main() {
scanf("%d",&T);
while (T--) {
scanf("%d",&n);
long long z=0,f=0;
ans=0;
for (int i=1;i<=n;i++) {
scanf("%d",&a[i]);
if (a[i]>0) {
z+=a[i];
if (f>=a[i]) f-=a[i];
else ans+=a[i]-f,f=0;
} else {
f-=a[i];
if (z>=-a[i]) z+=a[i];
else ans-=a[i]+z,z=0;
}
}
printf("%lld\n",ans);
}
return 0;
}
F. Laboratory on Pluto
Problem
题目大意：
在一个无限大的网格中，你要选择 \(n\) 个格子，使得其周长最小。
每个数据可能是以下两种情况：
\(Type = 1\)，则要求构造任意一种最优解。保证 \(\sum n \le 8 \times 10^5\)
\(Type = 2\)，则要求输出最小的周长和最优解的方案数。
Solution
首先考虑第一问，显然构造成下图的类似于矩形的形状一定不劣。
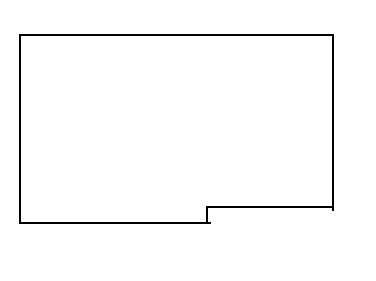
故可以枚举矩形的长宽中较小的一条的长度。
考虑第二问，显然最优解一定是一个矩形扣掉四个角，类似于下图。
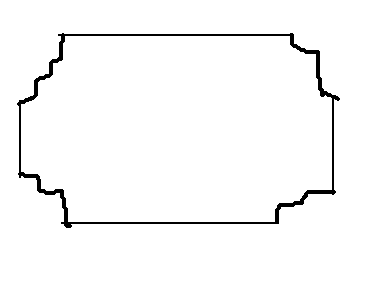
考虑单独一个角怎么做。
由于一个角上的空格成阶梯状，故可以将每行的格子数取下来形成一个单调不降的序列，于是数空格数为 \(k\) 的方案数变成了求有多少个单调不降的序列满足总和 \(=k\)。
这是一个经典的 DP，设 \(dp_{i,j}\) 表示长度为 \(i\)，总和为 \(j\) 的方案数。
转移方程分别对应往序列前面添加一个 \(1\) 和给整个序列 \(+1\)。
设 \(f_i\) 表示 \(i\) 个空格的答案，则
显然四个角上的答案都一样，所以最后把这四个卷起来即可。注意空格数是 \(O(\sqrt{n})\) 的，所以可以暴力卷积。
为什么这样不会出现同一个空格被两个角计算的情况？
注意到一个显然但是重要的结论：空格数不超过长宽的较小值。故不会算重。
但是注意到 \(\sum n \le 8 \times 10^5\) 只在 \(Type = 1\) 的时候成立，故还需要加一些优化。
- \(dp,f\) 和最终的答案显然可以预处理，这样预处理的复杂度为空格数的平方，即 \(O(n)\)。
- 枚举合法的矩形长宽也不能直接来，但是大胆猜想最优矩形一定在根号左右，故枚举根号前后 \(100\) 个即可。
Code
注意取模。
// Think twice, code once.
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int T,Type,n,mod;
void solve1() {
int len=1;
for (int i=2;i<=n;i++)
if (len+(n+len-1)/len>i+(n+i-1)/i) len=i;
int cnt=n;
printf("%d %d\n",len,(n+len-1)/len);
for (int i=1;i<=len;i++,puts(""))
for (int j=1;j<=(n+len-1)/len;j++)
if (cnt) putchar('#'),cnt--;
else putchar('.');
return ;
}
int dp[1005][1005];
int f[1005],g[1005],gg[1005];
void solve2() {
int len=1;
for (int i=max((int)sqrt(n)-100,1);i<=min((int)sqrt(n)+100,n);i++)
if (len+(n+len-1)/len>i+(n+i-1)/i) len=i;
printf("%d ",(len+(n+len-1)/len)*2);
// printf("\n%d %d\n",k,len);
// puts("");
int ans=0;
for (int r=max((int)sqrt(n)-100,1);r<=min((int)sqrt(n)+100,n);r++)
if (len+(n+len-1)/len==r+(n+r-1)/r) {
int c=(n+r-1)/r;
if (r>c) break;
int k=r*c-n;
ans=(ans+gg[k]*(r==c?1:2)%mod)%mod;
}
printf("%d\n",ans);
return ;
}
int main() {
scanf("%d%d",&T,&Type);
if (Type==2) {
scanf("%d",&mod);
dp[0][0]=1;
for (int i=1;i<=1000;i++)
for (int j=i;j<=1000;j++) {
if (i==j) {
dp[i][j]=1;
continue;
}
if (i>0) dp[i][j]=dp[i-1][j-1];
if (j>i) dp[i][j]=(dp[i][j]+dp[i][j-i])%mod;
}
f[0]=1;
for (int i=1;i<=1000;i++)
for (int j=1;j<=i;j++)
f[i]=(f[i]+dp[j][i])%mod;
for (int i=0;i<=1000;i++)
for (int j=0;j<=1000;j++)
if (i+j<=1000) g[i+j]=(g[i+j]+(long long)f[i]*f[j]%mod)%mod;
for (int i=0;i<=1000;i++)
for (int j=0;j<=1000;j++)
if (i+j<=1000) gg[i+j]=(gg[i+j]+(long long)f[i]*g[j]%mod)%mod;
for (int i=0;i<=1000;i++) g[i]=gg[i],gg[i]=0;
for (int i=0;i<=1000;i++)
for (int j=0;j<=1000;j++)
if (i+j<=1000) gg[i+j]=(gg[i+j]+(long long)f[i]*g[j]%mod)%mod;
}
while (T--) {
scanf("%d",&n);
if (Type==1) solve1();
else solve2();
}
return 0;
}
