KMP
[学习笔记]KMP
KMP 是啥?能次吗?
先来说明以下 KMP 是用来解决什么问题的。
就是用来解决字符串匹配问题的啦 QwQ~
具体地说,我们有一个文本和一个关键词,我们想要知道这个关键词在文本中的哪些位置出现了。KMP 就是用来解决这个问题的。
KMP 在生活中的应用十分广泛,例如编辑器的查找功能:
又比如,在 某LaTeX数学公式大全 里查找某个公式。又或者,在某个地方有一个很长很长的名单,你想知道某某某在不在这个名单中……
KMP 就是用来解决这类问题的。也就是说,会给你一个文本和一个关键词,要你求关键词在文本中出现的位置(位置即关键词的第一个字符在文本中的位置)。
小提示 \(\&\) 一些定义:
- 主串:上文提到的那个“文本”,在下文中可能会用 \(s\) 表示。
- 模式串:上文提到的那个“关键词”,在下文中可能会用 \(t\) 表示。
- \(n,m\):如无特殊说明则表示主串和模式串的长度。
- 下文中的 Code 均为 洛谷 P3375 【模板】KMP字符串匹配 的 Code,所以请时刻注意,输出的下标从 \(1\) 开始。
- 字符串下标从 \(0\) 开始。
Brute-Force 算法
顾名思义,Brute-Force 是一个很暴力的算法,也是一般初学者写字符串匹配会用且常用的算法。
其大概的过程就是枚举 \(s\) 的每个位置,以这个位置为起点截取一段长度为 \(m\) 的子串,将其与 \(t\) 比较,若相同,那么就是匹配到了。
于是我们可以快速地敲出 Brute-Force 的 Code:
for(int i=0;i<(int)s.length();i++)
{
bool flag=true;
for(int j=0;j<(int)t.length();j++)
if(s[i]!=s[j]){flag=false;break;}
if(flag==true) printf("%d\n",i+1);
}
然后我们分析它的时间复杂度,最坏情况下每次都会把内层循环执行完,也就是说,它的复杂度是 \(O(nm)\) 的,太慢了!
优化 Brute-Force
显然,对于每一个 \(s\) 上的位置,我们要判断它是否可行必须得把整个串扫一遍,这里看起来无法优化了,那么我们就尝试优化以下查找次数。
比如说我们有个主串“ABCABD...”,模式串“ABCABC”,那么我们执行以下 Brute-Force:

此时,我们需要考虑 \(s\) 的下标为 \(1,2\) 的情况吗?不需要,它们肯定不行。那么,我们怎么知道它要从哪个位置开始枚举呢?或者说,这个位置有什么特别的性质?相信细心的同学已经发现了,若在 \(i\) 失配,那么若 \(0\)~\(k\) 的子串与 \(i-k\)~\(i-1\) 的子串相同,则从 \(i-k\) 开始匹配。也就是这样:
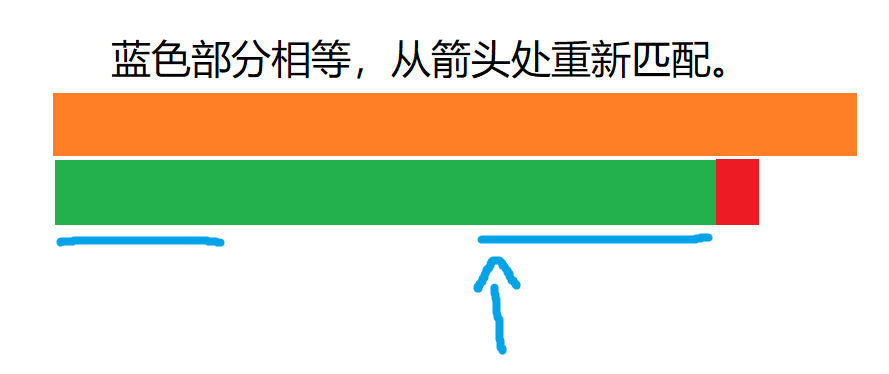
上图中橙色是主串,下面那条是模式串,红色是失配的地方。
这样,我们就减少了匹配次数。而这,就是 KMP 算法。
nxt 数组
我们设 字符串 \(P\) 的 \(nxt_i\) 表示 \(P_0\)~\(P_i\) 中,前 \(nxt_i\) 个字符与后 \(nxt_i\) 个字符相等。[1]
仔细观察可以发现,\(0\)~\(nxt_i-1\) 其实就是第一个蓝条的部分,而 \(i-nxt_i\)~\(i-1\) 则是第二个蓝条的部分。
相信细心的你已经发现了,没错,其实 \(nxt_i\) 就相当于上文提到的那个 \(k\)。
再看上面的那张图,我们在扫描时是将模式串移动到了后面那个蓝条条的位置,也就是这样:
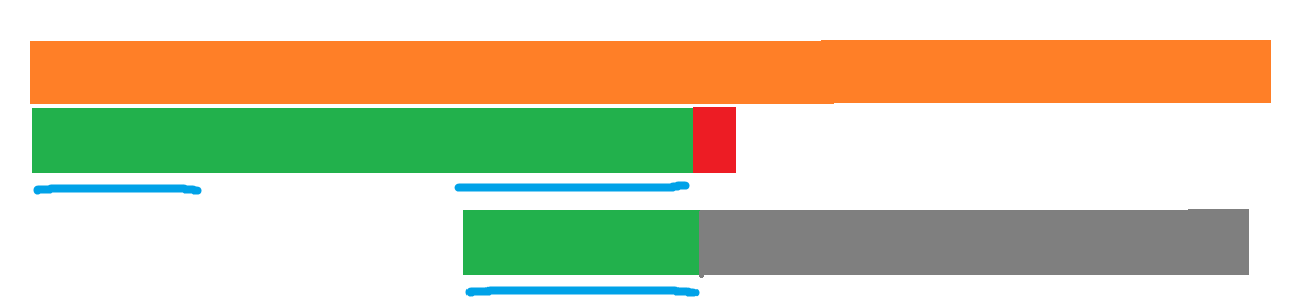
灰色部分是待匹配的。
再将移动对应到 \(nxt\) 数组,就能发现:若在 \(i\) 失配,就是把 \(nxt_{i-1}\) 移到 \(i\)(不要忘记下标是从 \(0\) 开始的)。所以,我们现在可以根据 \(nxt\) 数组来进行模式串的位置跳跃了。
具体实现
下面就到了最激动人心的实现环节力~
实现分两部分,一部分是求 \(nxt\) 数组,另一部分是查找。
这里先讲查找,因为求 \(nxt\) 数组是精髓,留到最后 QwQ。
查找
我们设 \(now\) 为当前在主串中的位置,而 \(pos\) 为当前在模式串中的位置。那么我们可以进行分类讨论:
如果 \(s_{now}=t_{pos}\),那么说明这一位可以匹配,直接让 \(now+1,pos+1\)。
否则,即 \(s_{now} \not= t_{pos}\),那么又要分两种情况讨论。如果 \(pos \not= 0\),那么直接用上面的方法进行跳跃,即 \(pos=nxt_{pos-1}\)。那么如果 \(pos=0\) 呢?说明第一位就匹配失败了,只能让 \(now+1\)。
最后,做完上面的三个判断之后,我们还要再判断一下:如果 \(pos=m\),那么就说明 \(0\)~\(m-1\) 每一位都可以匹配,也就是整个模式串都可以匹配,那不就匹配成功了吗?此时位置为 \(now-pos\)。那么接下来从哪里开始查找呢?\(now-pos+1\)?不,如果从 \(now-pos+1\) 开始找,那复杂度就和 Brute-Force 差不多了(如果匹配成功次数很多且模式串长度很大的话)。此时,我们其实可以认为模式串在位置 \(m\) 的地方失配了,那么因为 \(m \not =0\),所以使用第二种跳跃方式,即 \(pos=nxt_{pos-1}\)。
根据上面的这些描述,可以写出如下代码:
for(int pos=0,now=0;now<(int)s.length();)//now当然要小于n,否则还怎么匹配?
{
if(s[now]==t[pos]) now++,pos++;//第一种情况
else if(pos!=0) pos=nxt[pos-1];//第二种情况
else now++;//第三种情况
if(pos==(int)t.length())//匹配成功
{
printf("%d\n",now-pos+1);
pos=nxt[pos-1];
}
}
我们分析它的时间复杂度,是 \(O(n+m)\) 的。(因为主串和模式串的每个位置都被扫了且仅被扫了一遍)
求 nxt 数组
这里我们用递推的方式求,也就是知道 \(nxt_0,nxt_1,\cdots,nxt_{i-1}\),求 \(nxt_i\)。
假设我们现在已经知道了一个 \(k\),使得模式串中 \(0\)~\(k-1\) 与 \(i-k\)~\(i-1\) 相等(是不是很熟悉?),且 \(t_k=t_i\),也就是下面这张图:

那么,很明显 \(i=k+1\)(注意下标从 \(0\) 开始)。
这里我们插入一个定义:
- 前缀:从 \(0\) 开始截取的一段连续的区间组成的子串。
- 后缀:从末尾开始截取的一段连续的区间组成的子串。
那么为了找到这种情况,首先我们得保证 \(0\)~\(i-1\) 的子串中,它的长度为 \(k\) 的前缀与长度为 \(k\) 的后缀相等。但是这并不能保证 \(t_k=t_i\),此时就需要缩小 \(k\)。如何缩小?得保证 \(k\) 尽量大并满足之前的性质。
但我们还是没有思路。那么……
它的长度为 \(k\) 的前缀与长度为 \(k\) 的后缀相等。
是的,这里有一个很强的性质。缩小后的 \(k_{now}\) 一定可以保证现在的长度为 \(k_{now}\) 的前后缀在原来的长度为 \(k\) 的前后缀中(因为 \(k_{now}<k\) 嘛),而长度为 \(k\) 的前后缀又是相等的,所以 \(k_{now}\) 其实就是要是长度为 \(k\) 的前缀的 \(nxt\),即 \(nxt_k\)!
所以 \(k=nxt_{k-1}\)。
当然了,如果一直这么做直到 \(k=0\) 的话,说明 \(nxt_i=0\)。
for(int i=1;i<(int)t.length();i++)
{
int k=nxt[i-1];
while(t[k]!=t[i]&&k!=0) k=nxt[k-1];
if(t[k]==t[i]) nxt[i]=k+1;
else nxt[i]=0;
}
In the end
最后,附一下洛谷 P3375 【模板】KMP字符串匹配的完整代码:
//Luogu P3375
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
string s,t;
int nxt[1000005];
int main()
{
cin>>s>>t;
for(int i=1;i<(int)t.length();i++)
{
int k=nxt[i-1];
while(t[k]!=t[i]&&k!=0) k=nxt[k-1];
if(t[k]==t[i]) nxt[i]=k+1;
else nxt[i]=0;
}
for(int pos=0,now=0;now<(int)s.length();)
{
if(s[now]==t[pos]) now++,pos++;
else if(pos!=0) pos=nxt[pos-1];
else now++;
if(pos==(int)t.length())
{
printf("%d\n",now-pos+1);
pos=nxt[pos-1];
}
}
for(int i=0;i<(int)t.length();i++) printf("%d ",nxt[i]);
return 0;
}
在不同的地方 nxt 数组表示的意义有所不同。 ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号