dijkstra

\(dijkstra​\)怎么写：首先，是和\(SPFA​\)一样的初始化。然后，把起点标记为访问。然后更新与其相连的点的最短路的值（就是松弛）。再找到未访问的点中最短路的值最小的点，重复以上操作。
具体实现起来就是这个亚子：

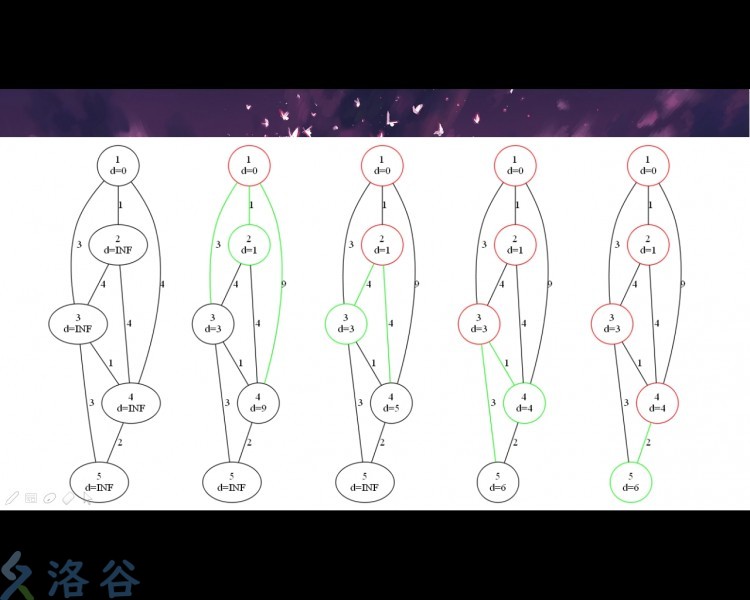
（图片来源于洛谷2019夏令营的课件）
讲完基础的，再来讲一下细节问题：这个细节决定了时间复杂度！
这个细节就是“找到未访问的点中最短路的值最小的点”。
两种方法：
第一种：非常实用的爆扫。时间复杂度是O(\(n^2​\))，个人感觉和\(SPFA​\)没有什么区别，不建议使用。
第二种：优先队列！该方法是当一个点的最短路的值被更新后，就将其加入小根堆。这时小根堆里会出现多个相同的点。但是我们用过一个点之后就会将其标记，所以不会有问题。时间复杂度是O(mlogn)
什么？你不知道小根堆是什么？戳这里
但我们是不会手打小根堆的，太麻烦了。于是，我们就要用到priority_queue。他是系统自带优先队列，但是是大根堆。而且我们是要按照每个点的值来排序的。但我们同时也要记录他的编号。

于是可以这样搞：

struct node
{
	int first,second;
	friend bool operator<(node x,node y){return x.first>y.first;}
};
priority_queue<node> q;

所有问题都解决了，那么上代码吧。

#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,s;
int v[100005];
bool f[100005];
struct node
{
	int first,second;
	friend bool operator<(node x,node y){return x.first>y.first;}
};
priority_queue<node> q;
struct graph
{
	int tot;
	int hd[100005];
	int nxt[200005],to[200005],dt[200005];
	void add(int u,int v,int w)
	{
		tot++;
		nxt[tot]=hd[u];
		hd[u]=tot;
		to[tot]=v;
		dt[tot]=w;
		return ;
	}
}g;
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		g.add(u,v,w);//建图
	}
	memset(v,0x3f,sizeof(v));//初始化
	q.push((node){0,s});//压入起点
	v[s]=0;
	while(!q.empty())
	{
		int xx=q.top().second;
		q.pop();
		if(!f[xx])//判断是否被访问过
		{
			f[xx]=true;//标记一下
			for(int i=g.hd[xx];i;i=g.nxt[i])
				if(v[g.to[i]]>v[xx]+g.dt[i])//松弛
		 		{
					v[g.to[i]]=v[xx]+g.dt[i];
					q.push((node){v[g.to[i]],g.to[i]});//加入小根堆
				}
		}
	}
	for(int i=1;i<=n;i++) printf("%d ",v[i]);
	return 0;
}