Johnson全源最短路
首先考虑求全源最短路的几种方法:
- Floyd:时间复杂度,可以处理负权边,但不能处理负环,而且速度很慢。
- Bellman-Ford:以每个点为源点做一次Bellman-Ford,时间复杂度,可以处理负权边,可以处理负环,但好像比Floyd还慢?
- dijkstra:以每个点为源点做一次dijkstra,时间复杂度,不能处理负权边,但比前面两个快多了。
好像……只有dijkstra还有希望?但负权边处理不了真是很棘手啊。
一种方法是让每条边都加上一个数使得边权为正,但考虑下图:
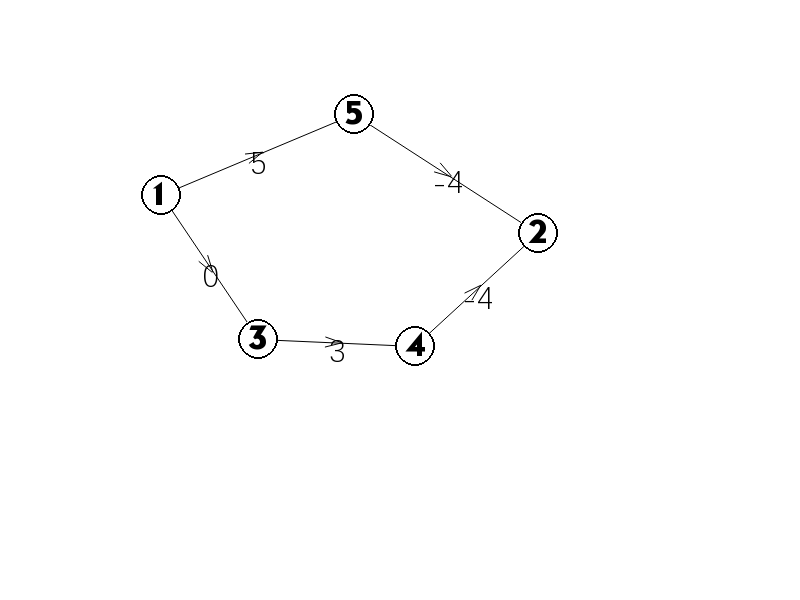
到的最短路应为:,长度为。如果我们把每条边的边权都加上:
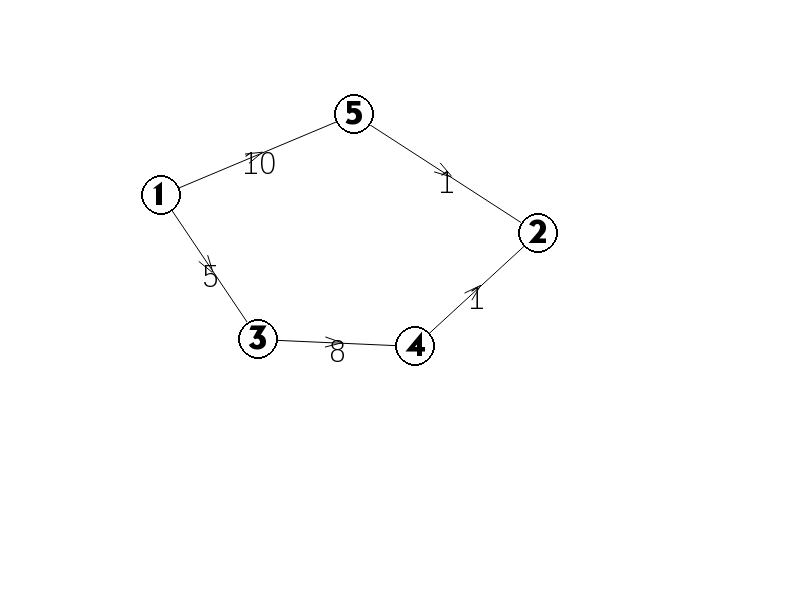
此时的最短路是:,就不是实际的最短路了,所以这种方法行不通
注:经本人研究,应该是两条路径进过的边的数量不同而导致的
接下来,就该 Johnson 登场啦!Johnson 其实就是用另一种方法标记边权啦。
首先来看看实现方法:我们新建一个虚拟结点(不妨设他的编号为0),由他向其他的所有结点都连一条边权为的边,然后求0号节点为源点的单源最短路,存到一个数组中。然后,让每条边的权值变为,这里和分别为这条边的起点和终点。然后再以每个点为源点做 dijkstra 就OK了。
Q:那这么说,Dijkstra 也可以求出负权图(无负环)的单源最短路径了?
A:没错。但是预处理要跑一遍 Bellman-Ford,还不如直接用 Bellman-Ford 呢。
如何证明这是正确的呢?
首先,从到的路径中随便取出一条:
则这条路径的长度为:
简化后得到:
可以发现,不管走哪条路径,最后都是,而和又是不变的,所以最终得到的最短路径还是原来的最短路径。
到这里已经证明一半了,接下来要证明得到的边权非负,必须要无负权边才能使 dijkstra 跑出来的结果正确。根据三角形不等式(就是那个三角形里任意两条边的长度之和大于等于另一条边的长度),新图上的任意一条边上的两点满足:,则新边的边权。所以新图的边权非负。
正确性证明就是这个亚子。
代码实现(注意处理精度问题,该开ll的时候开ll):
#include<cstdio>
#include<queue>
#define MAXN 5005
#define MAXM 10005
#define INF 1e9
using namespace std;
int n,m;
int vis[MAXN];
long long h[MAXN],dis[MAXN];
bool f[MAXN];
struct graph
{
int tot;
int hd[MAXN];
int nxt[MAXM],to[MAXM],dt[MAXM];
void add(int x,int y,int w)
{
tot++;
nxt[tot]=hd[x];
hd[x]=tot;
to[tot]=y;
dt[tot]=w;
return ;
}
}g;//链式前向星
bool SPFA(int s)//这里用了Bellman-Ford的队列优化
{
queue<int>q;
for(int i=1;i<=n;++i) h[i]=INF,f[i]=false;
h[s]=0;
f[s]=true;
q.push(s);
while(!q.empty())
{
int xx=q.front();
q.pop();
f[xx]=false;
for(int i=g.hd[xx];i;i=g.nxt[i])
if(h[g.to[i]]>h[xx]+g.dt[i])
{
h[g.to[i]]=h[xx]+g.dt[i];
if(!f[g.to[i]])
{
if(++vis[g.to[i]]>=n) return false;//注意在有重边的情况下要记录入队次数而不是松弛次数
f[g.to[i]]=true,q.push(g.to[i]);
}
}
}
return true;
}
void dijkstra(int s)
{
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
for(int i=1;i<=n;i++) dis[i]=INF,f[i]=false;
q.push(make_pair(0,s));
dis[s]=0;
while(!q.empty())
{
int xx=q.top().second;
q.pop();
if(!f[xx])
{
f[xx]=true;
for(int i=g.hd[xx];i;i=g.nxt[i])
if(dis[g.to[i]]>dis[xx]+g.dt[i])
{
dis[g.to[i]]=dis[xx]+g.dt[i];
if(!f[g.to[i]])
q.push(make_pair(dis[g.to[i]],g.to[i]));
}
}
}
return ;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
g.add(u,v,w);
}
for(int i=1;i<=n;i++) g.add(0,i,0);//建虚拟节点0并且往其他的点都连一条边权为0的边
if(!SPFA(0))//求h的同时也判了负环
{
printf("-1");
return 0;
}
for(int u=1;u<=n;u++)
for(int i=g.hd[u];i;i=g.nxt[i])
g.dt[i]+=h[u]-h[g.to[i]];//求新边的边权
for(int i=1;i<=n;i++)
{
dijkstra(i);//以每个点为源点做一遍dijkstra
long long ans=0;
for(int j=1;j<=n;j++)//记录答案
if(dis[j]==INF) ans+=1ll*j*INF;
else ans+=1ll*j*(dis[j]+(h[j]-h[i]));
printf("%lld\n",ans);
}
return 0;
}
最后安利一发博客



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】