树的重心
先看题:P1395会议
树的重心,就是在一棵树中拆掉一个点,把这棵树分成几个部分,使得最大的部分最小,亦即拆得均匀,这个拆掉的点就是树的重心。
那么怎么求呢?我们可以从根结点开始dfs(什么?你说是无根树。那就定义节点1为根呗),返回值是这棵子树的大小。然后定义一个\(mx\),\(mx=max\{dfs(\text{该结点的子结点的})\}\) 。最后,在枚举完子节点后,再判断他父亲那一块的大小。然后记录值。
现在唯一的问题就是父亲那块怎么解决呢?没错,用总结点数减去这棵子树的大小,就是他父亲那一块的大小。
现在来解决第二问 ,这问其实可以在解决树的重心后直接dfs或bfs,然后就可以得出总的路程了。这一块就不用详细解释了。
上代码:
#include<bits/stdc++.h>
using namespace std;
int n,ans=50005,sum=50005,road;//n是总结点数,ans是树的重心的编号,sum是其最那块的大小,road是总路程
int t[50005];//ti表示结点i到ans的距离。
queue<int>q;//q用来后面bfs用
struct graph
{
int tot;
int dt[100005],nxt[100005];
int hd[50005];
void add(int x,int y)
{
tot++;
nxt[tot]=hd[x];
hd[x]=tot;
dt[tot]=y;
}
}g;//graph是链式前向星。
int dfs(int x,int fa)
{
int k=0;//k代表其所以子树的大小
int mx=0;//mx是将这个点拆掉后最大那块的大小
for(int i=g.hd[x];i;i=g.nxt[i])//遍历所以点子节点
if(g.dt[i]!=fa)//注意判该节点是否是x的父亲,不判会爆栈的
{
int xx=dfs(g.dt[i],x);//记录这棵子树的大小
k+=xx;//加上这棵子树的大小
mx=max(mx,xx);//取最大值
}
mx=max(mx,n-k-1);//最后判一下父亲那块,最后的-1是因为最开始没有把自己算进去
if(mx<sum||(mx==sum&&x<ans)) sum=mx,ans=x;//如果比当前方案更优,就取这个方案
return k+1;//返回整棵子树的大小
}
void bfs()
{
q.push(ans);//记录最初的点
while(!q.empty())//如果队列不为空
{
int xx=q.front();//记录队首
q.pop();//弹出队首
for(int i=g.hd[xx];i;i=g.nxt[i])//遍历链接它的节点
{
int yy=g.dt[i];
if(t[yy]||yy==ans) continue;//如果这个点已经被遍历过,continue
t[yy]=t[xx]+1;//记录距离
road+=t[yy];//总距离要加上这个点的距离
q.push(yy);//放进队列
}
}
return ;
}
int main()
{
cin>>n;
for(int i=1;i<n;i++)
{
int from,to;
cin>>from>>to;
g.add(from,to);
g.add(to,from);
}//输入+存图,注意是双向边
dfs(1,0);//dfs,把1的父亲设为0,就是没有父节点了(因为没有节点0)
bfs();//求出树的重心后,求总路程
cout<<ans<<' '<<road;
return 0;
}

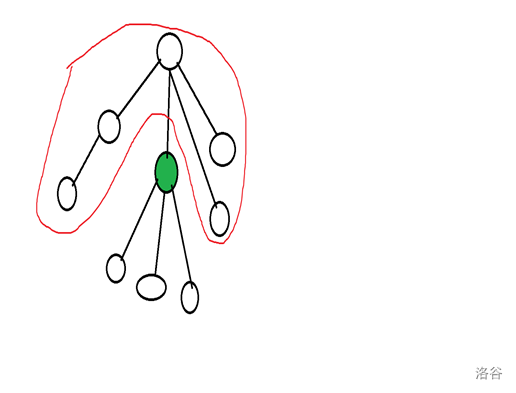 树的重心,就是在一棵树中拆掉一个点,把这棵树分成几个部分,使得最大的部分最小,亦即拆得均匀,这个拆掉的点就是树的重心。
树的重心,就是在一棵树中拆掉一个点,把这棵树分成几个部分,使得最大的部分最小,亦即拆得均匀,这个拆掉的点就是树的重心。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号