二分图匹配

题目：二分图匹配
二分图匹配，就是解决 一群人，喜欢一类东西，然后求最多满足能满足多少人的问题。当然，东西是不同的，人的喜好也是不同的。

这里讲一下匈牙利算法是如何解决这个问题的。
首先，我们画了一个图：

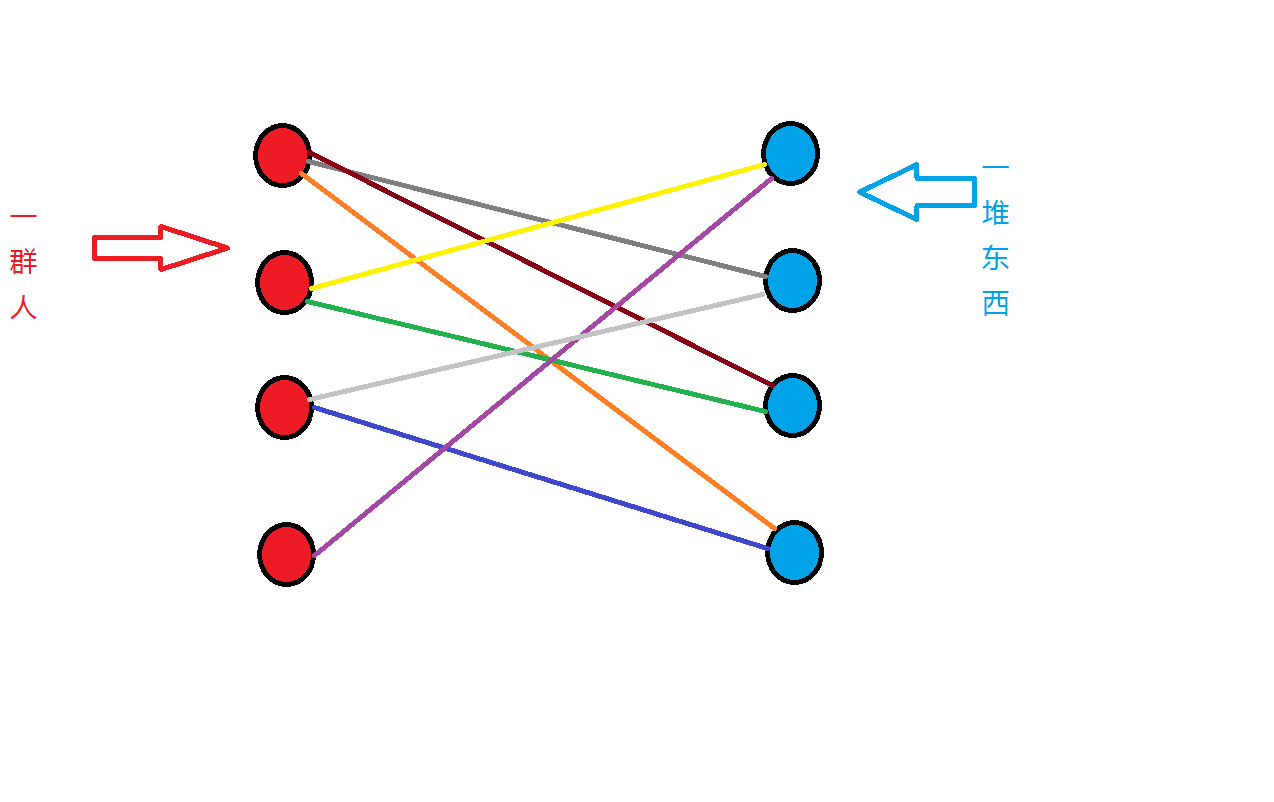
然后，我们对第一个人匹配，也就是找第一个人要的东西，然后就得到了下图（粉色代表匹配成功，也就是左边的人得到了右边的东西。草绿色代表遍历过但未成功）

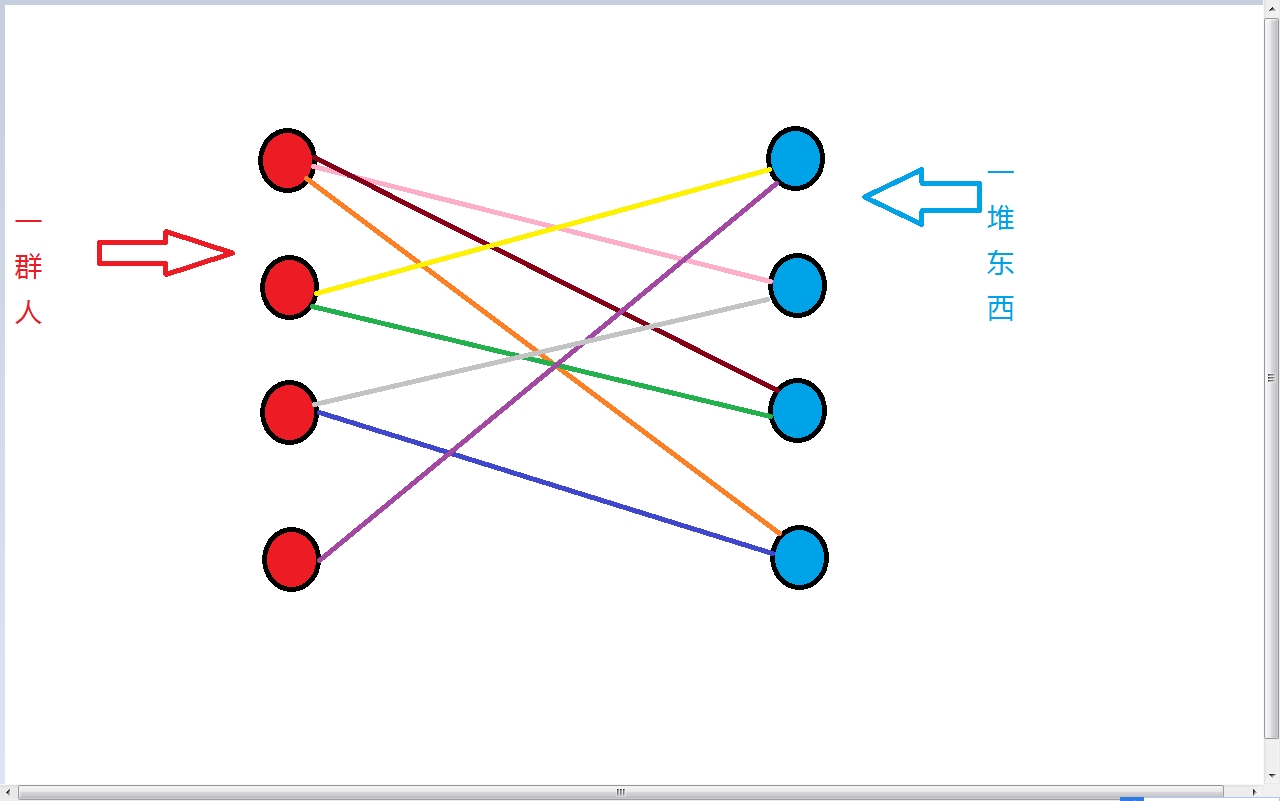
然后，我们跳过一大堆已知的操作，得到下图：

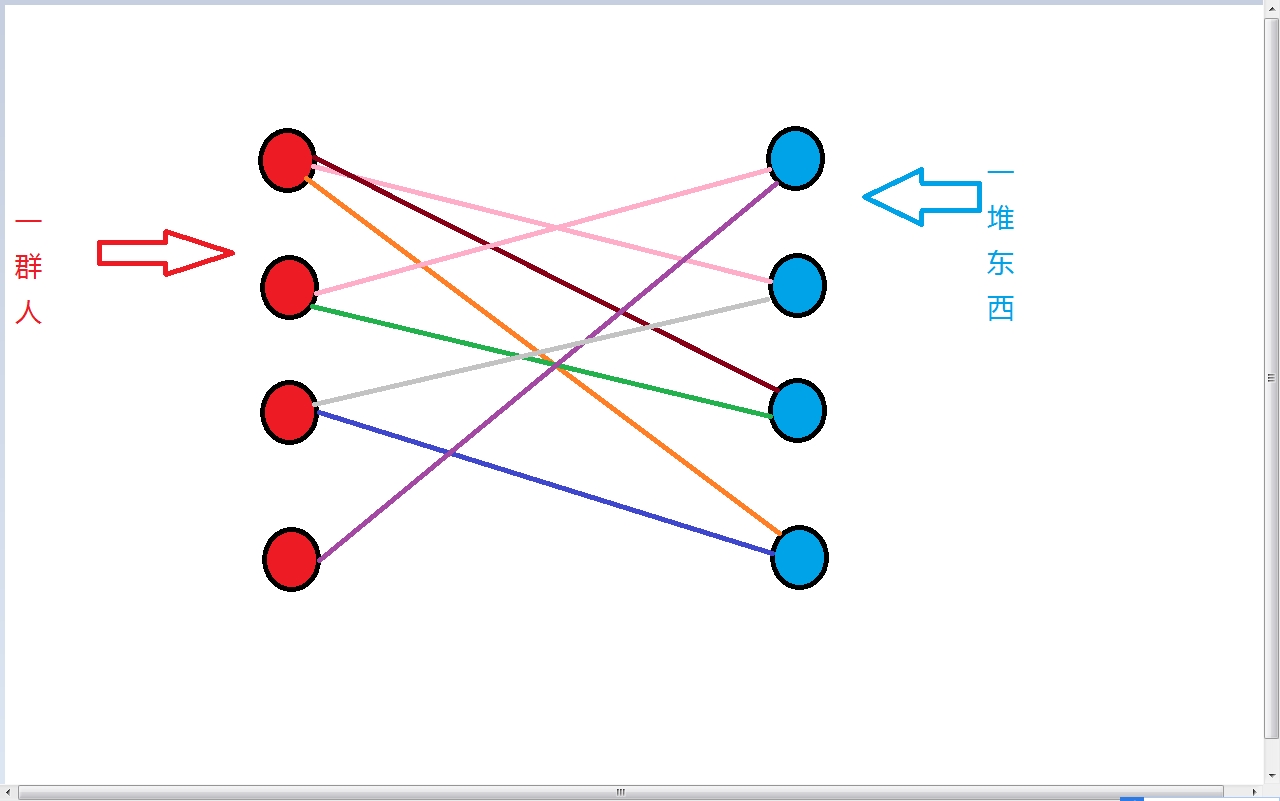
这时，我们发现，3号人也想要二号物品，但是已经被1号人拿走了。这改怎么办办呢？我们发现，1号还能拿3号物品。于是，人1把物2给了人3，拿了物3。

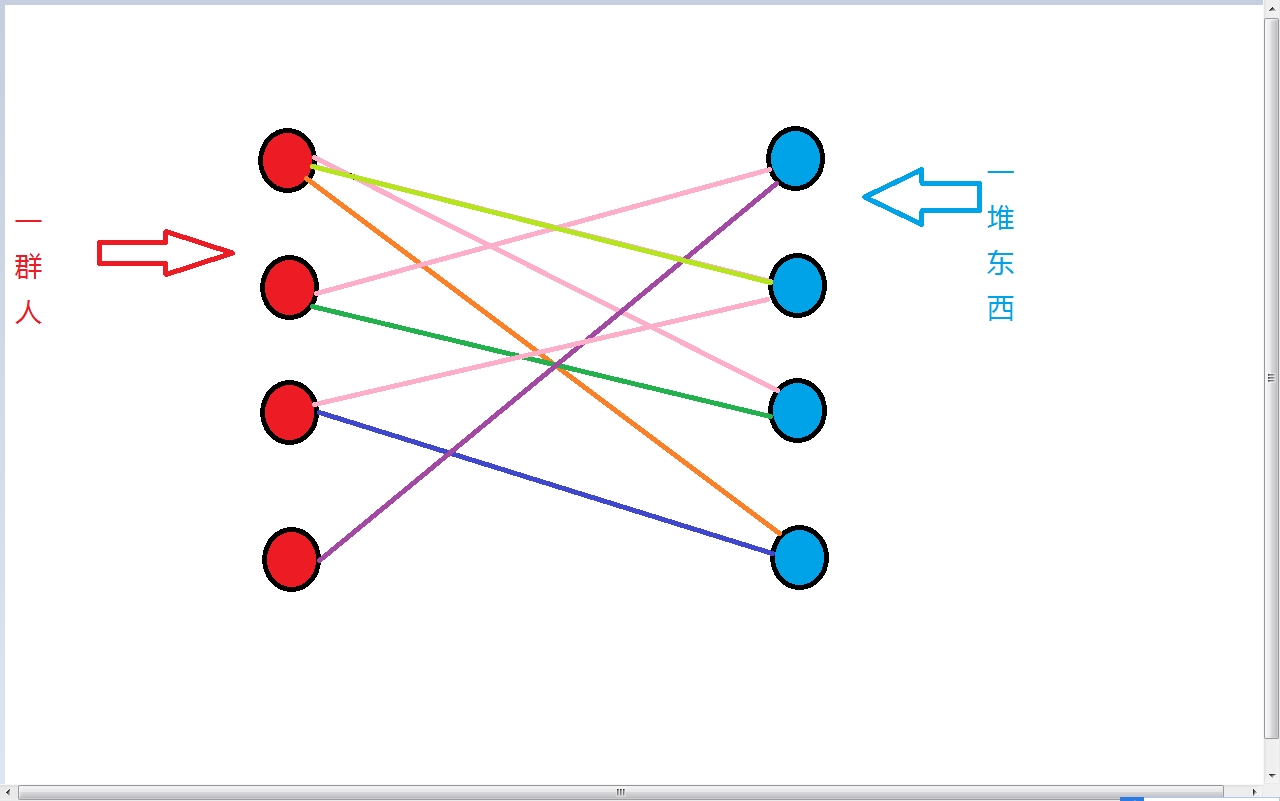
然后， 匹配4号。这时……人2占了物1，但人2不能拿别的东西了。于是乎，人2拒绝妥协，人4被人2暴打了一顿而人4匹配不了其他的，因为他对物品1情有独钟，不喜欢别的东西，so，他莫得东西了QwQ。

现在，所有的人都匹配完了，能拿到东西的最多有三个人，4号被抛弃了，还被暴打了一顿，最大匹配数也就是3。

那么，具体思路讲完了，改怎么实现呢？
很简单，我们逐个枚举人，\(dfs(i)=1\)表示匹配成功，否则失败。用\(1\)个\(chos\)数组，\(chos_i\)表示第\(i\)个物品被第\(chos_i\)个人拿走了，\(vis\)数组用来在判断一个人能否拿别的物品时用的。也就是做个标记，如果不做这个标记，那再判断这个人能否拿别的物品时他也许还会选择这个物品。（所以，每次\(dfs\)都要清空\(vis\)）\(dfs\)内部就是枚举他喜欢的每一个东西，如果这个东西没人要或要这个东西的人可以拿别的，这个东西就归他了，然后返回1。如果遍历完所有他想要的还得不到任何东西，就返回0。
\(vis\)数组要在每一次遍历的时候清空哦

上代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,e,ans;//e是边数，ans是答案
bool vis[100005];
int chos[100005];
struct node
{
	int tot;
	int dt[10000005],nxt[10000005];
	int hd[100005];
	void add(int x,int y)
	{
		tot++;
		nxt[tot]=hd[x];
		hd[x]=tot;
		dt[tot]=y;
		return ;
	}
}g;//链式前向星存图
bool dfs(int x)
{
	for(int i=g.hd[x];i;i=g.nxt[i])//枚举他喜欢的每一个东西
	{
		if(vis[g.dt[i]]) continue;//被判断过，就直接下一个循环
		vis[g.dt[i]]=1;//标记，如果不标记，后面的判断dfs(chos[g.dt[i]])就永远是真了。
		if(!chos[g.dt[i]]||dfs(chos[g.dt[i]]))//如果当前没人要这个东西或要这个东西的人还可以拿别的，那这个东西就是他的了
		{
			chos[g.dt[i]]=x;//标记这个东西归他了
			return 1;//返回true。
		}
	}
	return 0;//到遍历完还没得到东西，返回false
}
int main()
{
	scanf("%d%d%d",&n,&m,&e);
	for(int i=1;i<=e;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		if(u>n||v>m) continue;//题目中说有可能会出现u>n和v>m的情况
		g.add(u,v);//连边
	}
	for(int i=1;i<=n;i++)//枚举每个人
	{
		memset(vis,0,sizeof(vis));//清空vis
		ans+=dfs(i);//直接加就可以了，因为bool中true的值是1，false的值是0
	}
	printf("%d",ans);
	return 0;
}