【BZOJ2882】【字符串的最小表示】工艺
题目描述
小敏和小燕是一对好朋友。他们正在玩一种神奇的游戏,叫Minecraft。他们现在要做一个由方块构成的长条工艺品。但是方块现在是乱的,而且由于机器的要求,他们只能做到把这个工艺品最左边的方块放到最右边。他们想,在仅这一个操作下,最漂亮的工艺品能多漂亮。两个工艺品美观的比较方法是,从头开始比较,如果第i个位置上方块不一样那么谁的瑕疵度小,那么谁就更漂亮,如果一样那么继续比较第i+1个方块。如果全都一样,那么这两个工艺品就一样漂亮。
前几天刚A掉的题..
一看题目就后缀数组敲起来了..贴一贴代码~
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#include<cstdio>#include<cstdlib>#include<cstring>#include<algorithm>#define INF 1000000007#define N 1200010using namespace std;int n,a[N],s[N],tmp[N],rank[N],sa[N];void suffix_array(){ int sz=N; for (int i=0;i<n;i++) rank[i]=a[i]; for (int i=0;i<sz;i++) s[i]=0; for (int i=0;i<n;i++) s[rank[i]]++; for (int i=1;i<sz;i++) s[i]+=s[i-1]; for (int i=n-1;i>=0;i--) sa[--s[rank[i]]]=i; for (int j=1;j<=n/4;j*=2){ int p=0; for (int i=n-j;i<n;i++) tmp[p++]=i; for (int i=0;i<n;i++) if (sa[i]-j>=0) tmp[p++]=sa[i]-j; for (int i=0;i<sz;i++) s[i]=0; for (int i=0;i<n;i++) s[rank[i]]++; for (int i=1;i<sz;i++) s[i]+=s[i-1]; for (int i=n-1;i>=0;i--) sa[--s[rank[tmp[i]]]]=tmp[i]; p=0;tmp[sa[0]]=0; for (int i=1;i<n;i++){ int v0=sa[i-1],v1=sa[i],v00,v01; if (v0+j<n) v00=rank[v0+j];else v00=-1; if (v1+j<n) v01=rank[v1+j];else v01=-1; if (rank[v0]==rank[v1]&&v00==v01) tmp[sa[i]]=p;else tmp[sa[i]]=++p; } for (int i=0;i<n;i++) rank[i]=tmp[i]; }}int main(){ scanf("%d",&n); for (int i=0;i<4*n;i++) a[i]=N/2; for (int i=0;i<n;i++) scanf("%d",&a[i]),a[n+i]=a[i]; n*=4;suffix_array(); for (int i=sa[0];i-sa[0]<(n/4)-1;i++) printf("%d ",a[i]); printf("%d",a[sa[0]+(n/4)-1]); return 0;} |
今天晚上看了周源的《浅析“最小表示法”思想在字符串循环同构问题中的应用》
讲得很清楚很容易理解 但是等写完了以后才发现居然这么神奇~
一个长度为n的字符串s,假设其最小表示为s[M(s)..n]+s[1..M(s)-1]
只需要维护一个指针i使得i<=M(s)总成立并且逐渐接近M(s),以及一个用来辅助的指针j并且保证i<j
我的理解j的目的是在i的位置以后试图找到一个优于i的表示
并且如果存在这样一个优于i的表示的起始点p,满足j<=p
这样在情况②和④的时候似乎才说得通一些
为了保证每个表示都在字符串中出现一次,我们令s=s+s
开始时指针的状态为i,j,一直向右匹配直到其失配位置假设此时指针滑过k个位置
①
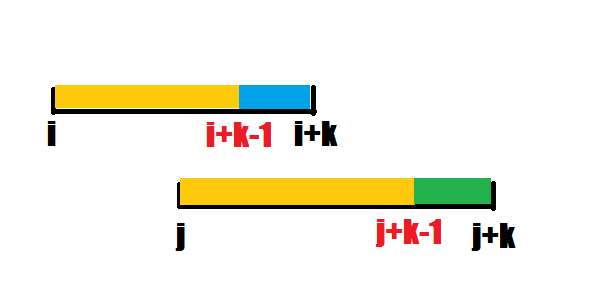
s[i..i+k-1]=s[j..j+k-1]且s[i+k]>s[j+k]时
显然i..i+k都不能为最小表示的起始位置,因为都可以在j..j+k中找到对应的且优于它的表示
因此i+k+1位置仍能保证<=M(s)
②
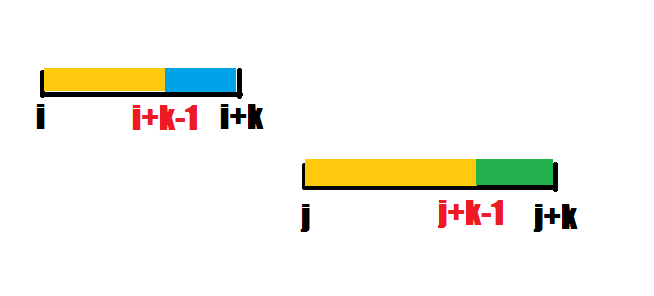
s[i..i+k-1]=s[j..j+k-1]且s[i+k]<s[j+k]时,与①类似可得到
以j+t为起点的表示一定劣于以i+t为起点的表示(t∈[0,k])
而当前指针指向j这个位置,根据指针j的定义可知,i+1..j-1中存在比i更优的表示已被排除,所以可以进一步得到
以j+t为起点的表示一定劣于以i为起点的表示(t∈[0,k])
所以j+k+1位置仍满足指针j的性质
③
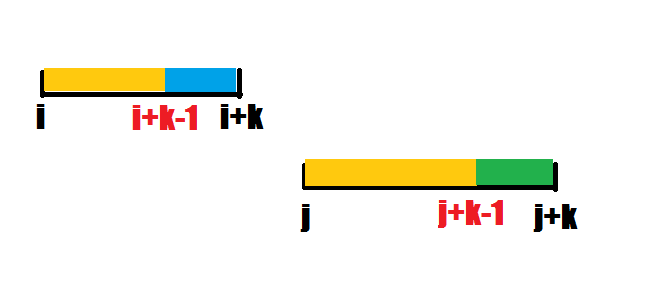
大致情况与①相同,当s[i+k]>s[j+k]且i+k+1<j时
显然i+1..j-1中已经不可能存在比i更优的表示,所以i可以直接滑到j
在①③两种情况中,i指针移动之后j指针指向的位置变为i+1
④什么时候结束?
(1)j指针指向了>n的位置,也就意味着i+1..n间不存在比i更优的表示了
此时i指针指向的位置就是字符串最小表示的起始点!
(2)j+k>2*n
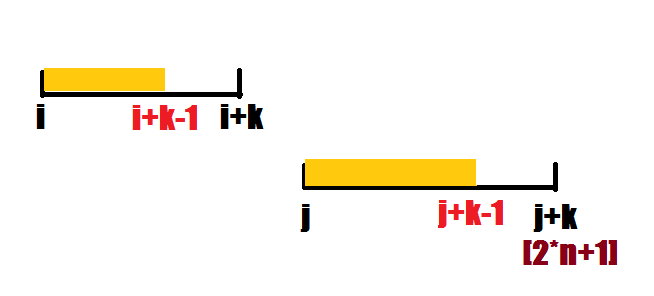
s[i..i+k-1]=s[j..j+k-1]
以j+t为起始点的表示不优于以i+t为起始点的表示(j+t<=n)
以i..j-1为起始点的表示不优于以i为起始点的表示
根据上面两条就可以同样得到此时i指针指向的位置就是字符串最小表示的起始点!
代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include<cstdio>#include<cstdlib>#include<cstring>#include<algorithm>using namespace std;int n,a[600010];int main(){ scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d",&a[i]),a[n+i]=a[i]; int i,j; for (i=1,j=2;j<=n;){ int k=0; while (j+k<=2*n&&a[i+k]==a[j+k]) k++; if (j+k>2*n) break; if (a[i+k]>a[j+k]) i=max(j,i+k+1),j=i+1;else j=j+k+1; } for (int j=0;j<n-1;j++) printf("%d ",a[j+i]);printf("%d",a[i+n-1]);} |
不论时间还是代码长度上都有很大的改进~



