HDU 5215 Cycle

Cycle

http://acm.hdu.edu.cn/showproblem.php?pid=5215

题意：

　　判断图中是否有奇环，偶环。

分析：

　　奇环直接判是不是二分图，黑白染色，如果一个点被染了两次，且不同色，那么存在奇环，否则不存在奇环。

　　偶环分为两种情况：1、如果在染色的过程中，一个点染了两次，且同色，那么存在偶环。2、两个奇环如果有相交的部分，那么一定存在偶环。

　　

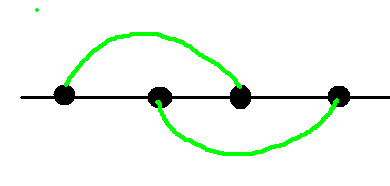
第一种情况：1-2-4-3-1是一个偶环。无论中间的部分存在几条边，由于两个奇环加起来一定是偶环，中间的部分*2也是偶数，一定也是也一个偶环。

第二种情况：1-2-3-1是一个偶环。奇数+奇数=偶数。

代码：

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<cmath>
 5 #include<iostream>
 6 #include<cctype>
 7 #include<set>
 8 #include<vector>
 9 #include<queue>
10 #include<map>
11 #define fi(s) freopen(s,"r",stdin);
12 #define fo(s) freopen(s,"w",stdout);
13 using namespace std;
14 typedef long long LL;
15 
16 inline int read() {
17     int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
18     for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f;
19 }
20 
21 const int N = 100005;
22 
23 int head[N], nxt[N * 6], to[N * 6], En;
24 int col[N], fa[N], tag[N];
25 bool f1, f2;
26 
27 void add_edge(int u,int v) {
28     ++En; to[En] = v; nxt[En] = head[u]; head[u] = En;
29     ++En; to[En] = u; nxt[En] = head[v]; head[v] = En;
30 }
31 
32 bool Merge(int u,int p) {
33     while (u != p && u) { // while (u != p) ??? 
34         if (tag[u]) return true;
35         tag[u] ++;
36         u = fa[u];
37     }
38     return false;
39 }
40 
41 void Color(int u) {
42     for (int i=head[u]; i; i=nxt[i]) {
43         int v = to[i];
44         if (v == fa[u]) continue;
45         if (col[v] == -1) {
46             col[v] = col[u] ^ 1;
47             fa[v] = u;
48             Color(v);
49         }
50         else {
51             if (col[v] == col[u]) {
52                 f1 = true; 
53                 if (Merge(u, v)) f2 = true;
54             }
55             else f2 = true;
56         }
57     }
58 }
59 
60 void init() {
61     f1 = f2 = 0;
62     En = 0;
63     memset(col, -1, sizeof(col));
64     memset(head, 0, sizeof(head));
65     memset(tag, 0, sizeof(tag));
66     memset(fa, 0, sizeof(fa));
67 }
68 void solve() {
69     init();
70     int n = read(), m = read();
71     for (int i=1; i<=m; ++i) {
72         int u = read(), v = read();
73         add_edge(u, v);
74     }
75     for (int i=1; i<=n; ++i) {
76         if (col[i] == -1) {
77             col[i] = 0;
78             Color(i);
79         }
80     }
81     puts(f1 ? "YES" : "NO");
82     puts(f2 ? "YES" : "NO");
83 }
84 
85 int main() {
86     int T = read();
87     while (T--) solve();
88     return 0;
89 }

 

posted @ 2018-10-09 16:37  MJT12044  阅读(199)  评论(0)  编辑  收藏  举报