#386. 【UNR #3】鸽子固定器
#386. 【UNR #3】鸽子固定器
分析:
神奇的做法+链表。
首先按照大小排序。
对于小于选择小于m个物品的时候,这个m个物品一定是一段连续的区间。因为,如果中间空着一个物品没选,而有没选到m个,还可以再选,于是选上空着的,不会增加花费,还增加了价值,所以可以直接枚举一个左端点,一个右端点,确定所有长度小于等于m个区间,然后计算即可。
如果等于m个物品,在上面的区间上可能不是连续的了。于是我们考虑选的这m个物品中的牢固度最小的x,然后再选m-1的物品(牢固度)比它大的。此时,我们把小于它的可以忽略了,假设当前的序列是上面拍完序后只保留了大于这个物品的牢固度的物品。然后在此序列上这m个物品又是一段连续的区间,(x的位置向左m个,向右m个,在此的一段连续的区间)。
选的方案如下图,区间为先按大小排好序,然后去掉牢固度比x小的物品,m个物品的牢固度都比x大,选的方案就是蓝色部分:
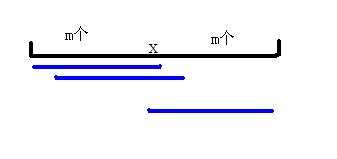
如果不是一段连续的区间:
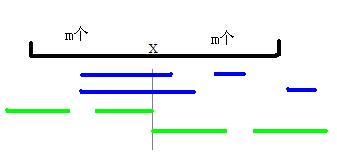
四种情况,如果是蓝色的情况,那么选中间空着的一定比选x优,牢固度大于x(超出m的部分也是大于x的,小于x的去掉了)
如果是绿色的情况,x作为端点,发现,如果选空着的,牢固度不仅大于x,而且,区间长度还会缩小,也就是大小的极差也会减小,所以x无法被选上。
所以对于必须且且最小值是x的,选的m个物品,必须是以x为中心,向左向右连续的一段区间。
所以我们可以依次从小到大枚举x,然后用链表维护删除的过程,那么剩下的物品就是一定大于x的。然后枚举这m个区间,就可以了。
代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<cmath> 5 #include<iostream> 6 #include<cctype> 7 #include<set> 8 #include<vector> 9 #include<queue> 10 #include<map> 11 using namespace std; 12 typedef long long LL; 13 14 inline int read() { 15 int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; 16 for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f; 17 } 18 19 const int N = 200100; 20 21 struct Node{ 22 int s, v, id; 23 }A[N], B[N], C[N]; 24 int L[N], R[N]; 25 LL s[N]; 26 int ds, dv; 27 28 bool cmp1(Node A, Node B) { 29 return A.s < B.s; 30 } 31 bool cmp2(Node A, Node B) { 32 return A.v < B.v; 33 } 34 LL Calc(LL v, LL s) { 35 if (dv == 2) v = 1ll * v * v; 36 if (ds == 2) s = 1ll * s * s; 37 return v - s; 38 } 39 void del(int p) { 40 R[L[p]] = R[p]; 41 L[R[p]] = L[p]; 42 } 43 int main() { 44 int n = read(), m = read(); ds = read(), dv = read(); 45 for (int i=1; i<=n; ++i) A[i].s = read(), A[i].v = read(); 46 sort(A + 1, A + n + 1, cmp1); //--- 47 for (int i=1; i<=n; ++i) A[i].id = i, B[i] = A[i]; 48 LL Ans = 0; 49 for (int i=1; i<=n; ++i) { 50 LL sum = 0; 51 for (int j=i; j<=(i+m-1)&&j<=n; ++j) { 52 sum += A[j].v; 53 Ans = max(Ans, Calc(sum, A[j].s - A[i].s)); 54 } 55 } 56 sort(A + 1, A + n + 1, cmp2); 57 for (int i=1; i<=n; ++i) L[i] = i - 1, R[i] = i + 1; 58 L[n + 1] = n, R[0] = 1; 59 60 for (int i=1; i<=n; ++i) { 61 int p = 0; 62 for (int j=A[i].id,k=1; j>=1&&k<=m; j=L[j],++k) C[++p] = B[j]; 63 reverse(C + 1, C + p + 1); 64 for (int j=R[A[i].id],k=2; j<=n&&k<=m; j=R[j],++k) C[++p] = B[j]; 65 for (int j=1; j<=p; ++j) s[j] = s[j - 1] + C[j].v; 66 for (int j=m; j<=p; ++j) 67 Ans = max(Ans, Calc(s[j] - s[j - m], C[j].s - C[j - m + 1].s)); 68 del(A[i].id); 69 } 70 cout << Ans; 71 return 0; 72 }


