hihocoder #1394 : 网络流四·最小路径覆盖(最小路径覆盖)
#1394 : 网络流四·最小路径覆盖
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
国庆期间正是旅游和游玩的高峰期。
小Hi和小Ho的学习小组为了研究课题,决定趁此机会派出若干个调查团去沿途查看一下H市内各个景点的游客情况。
H市一共有N个旅游景点(编号1..N),由M条单向游览路线连接。在一个景点游览完后,可以顺着游览线路前往下一个景点。
为了避免游客重复游览同一个景点,游览线路保证是没有环路的。
每一个调查团可以从任意一个景点出发,沿着计划好的游览线路依次调查,到达终点后再返回。每个景点只会有一个调查团经过,不会重复调查。
举个例子:
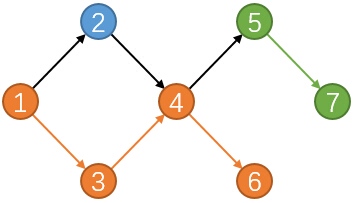
上图中一共派出了3个调查团:
1. 蓝色:调查景点;2
2. 橙色:调查景点;1->3->4->6
3. 绿色:调查景点;5->7
当然对于这个图还有其他的规划方式,但是最少也需要3个调查团。
由于小组内的人数有限,所以大家希望调查团的数量尽可能少,同时也要将所有的景点都进行调查。
当然,如何规划调查团线路的任务落到了小Hi和小Ho的头上。
输入
第1行:2个整数N,M。1≤N≤500,0≤M≤20,000。
第2..M+1行:2个数字u,v,表示一条有向边(u,v)。保证不会出现重复的边,且不存在环。
输出
第1行:1个整数,表示最少需要的调查团数量。
- 样例输入
-
7 7 1 2 1 3 2 4 3 4 4 5 4 6 5 7
- 样例输出
-
3
分析
最小路径覆盖=N-最大匹配数
code
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 5 using namespace std; 6 const int N = 1010; 7 const int INF = 1e9; 8 struct Edge{ 9 int to,nxt,c; 10 Edge() {} 11 Edge(int x,int y,int z) {to = x,c = y,nxt = z;} 12 }e[50010]; 13 int q[50100],L,R,S,T,tot = 1; 14 int dis[N],cur[N],head[N]; 15 16 inline char nc() { 17 static char buf[100000],*p1 = buf,*p2 = buf; 18 return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2) ? EOF :*p1++; 19 } 20 inline int read() { 21 int x = 0,f = 1;char ch=nc(); 22 for (; ch<'0'||ch>'9'; ch=nc()) if(ch=='-')f=-1; 23 for (; ch>='0'&&ch<='9'; ch=nc()) x=x*10+ch-'0'; 24 return x*f; 25 } 26 void add_edge(int u,int v,int c) { 27 e[++tot] = Edge(v,c,head[u]);head[u] = tot; 28 e[++tot] = Edge(u,0,head[v]);head[v] = tot; 29 } 30 bool bfs() { 31 for (int i=1; i<=T; ++i) cur[i] = head[i],dis[i] = -1; 32 L = 1,R = 0; 33 q[++R] = S;dis[S] = 1; 34 while (L <= R) { 35 int u = q[L++]; 36 for (int i=head[u]; i; i=e[i].nxt) { 37 int v = e[i].to; 38 if (dis[v] == -1 && e[i].c > 0) { 39 dis[v] = dis[u]+1;q[++R] = v; 40 if (v==T) return true; 41 } 42 } 43 } 44 return false; 45 } 46 int dfs(int u,int flow) { 47 if (u==T) return flow; 48 int used = 0; 49 for (int &i=cur[u]; i; i=e[i].nxt) { 50 int v = e[i].to; 51 if (dis[v] == dis[u] + 1 && e[i].c > 0) { 52 int tmp = dfs(v,min(flow-used,e[i].c)); 53 if (tmp > 0) { 54 e[i].c -= tmp;e[i^1].c += tmp; 55 used += tmp; 56 if (used == flow) break; 57 } 58 } 59 } 60 if (used != flow) dis[u] = -1; 61 return used; 62 } 63 int dinic() { 64 int ret = 0; 65 while (bfs()) ret += dfs(S,INF); 66 return ret; 67 } 68 69 int main() { 70 int n = read(),m = read(); 71 S = n + n + 1,T = n + n + 2; 72 for (int i=1; i<=n; ++i) add_edge(S,i,1),add_edge(i+n,T,1); 73 for (int i=1; i<=m; ++i) { 74 int u = read(),v = read(); 75 add_edge(u,v+n,1); 76 } 77 int ans = dinic(); 78 printf("%d",n-ans); 79 return 0; 80 }


