P2144 [FJOI2007]轮状病毒

P2144 [FJOI2007]轮状病毒

题目描述

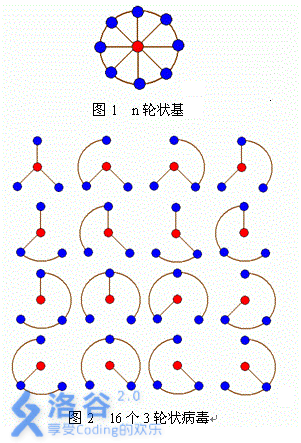
轮状病毒有很多变种。许多轮状病毒都是由一个轮状基产生。一个n轮状基由圆环上n个不同的基原子和圆心的一个核原子构成。2个原子之间的边表示这2个原子之间的信息通道，如图1。

n轮状病毒的产生规律是在n轮状基中删除若干边，使各原子之间有唯一一条信息通道。例如，共有16个不同的3轮状病毒，入图2所示。

给定n(N<=100)，编程计算有多少个不同的n轮状病毒。

输入输出格式

输入格式：

 

第一行有1个正整数n。

 

输出格式：

 

将编程计算出的不同的n轮状病毒数输出

 

输入输出样例

输入样例#1： 复制

3

输出样例#1： 复制

16

分析

首先想到的是生成树计数，数据范围也刚刚好，然后不过。

在网上看到大神一个神奇的式子：F(n)为n轮状病毒的个数，F(n) = 3F(n - 1) - F(n - 2) + 2

也可以搜索，打表，找规律。。。orz

不过需要高精度。。于是找到了一个Python代码。

code

python

n=int(raw_input())  
f=[0]*105  
f[1]=1  
for i in range(2,101):  
    f[i]=3*f[i-1]-f[i-2]+2  
print(f[n])  

 

40分Matrix-tree定理求生成树计数。

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>

using namespace std;
const double eps = 1e-12;
double c[110][110],ans;
int n;

void build() {
    int M = n+1;
    for (int i=1; i<n; ++i) c[i][i+1] = c[i+1][i] = -1;
    c[n][1] = c[1][n] = -1;
    for (int i=1; i<=n; ++i) {
        c[i][i] = 3;
        c[i][M] = c[M][i] = -1;
    }
    c[M][M] = n;
}
void Gauss() {
    for (int k=1; k<=n; ++k) {
        int r = k;
        for (int i=k+1; i<=n; ++i) 
            if (fabs(c[i][k]) > fabs(c[r][k])) r = i;
        if (r != k) for (int j=1; j<=n; ++j) swap(c[r][j],c[k][j]);
        for (int i=k+1; i<=n; ++i) 
            if (fabs(c[i][k]) > eps) {
                double t = c[i][k] / c[k][k];
                for (int j=k; j<=n; ++j) c[i][j] -= t*c[k][j];
            }
    }
    ans = 1.0;
    for (int i=1; i<=n; ++i) ans *= c[i][i];
    ans = ans<0?-ans:ans;
}
int main() {
    scanf("%d",&n);
    build(); 
    Gauss();
    printf("%.0lf\n",ans+eps);
    return 0;
}