P1126 机器人搬重物
题目描述
机器人移动学会(RMI)现在正尝试用机器人搬运物品。机器人的形状是一个直径1.6米的球。在试验阶段,机器人被用于在一个储藏室中搬运货物。储藏室是一个N*M的网格,有些格子为不可移动的障碍。机器人的中心总是在格点上,当然,机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有:向前移动1步(Creep);向前移动2步(Walk);向前移动3步(Run);向左转(Left);向右转(Right)。每个指令所需要的时间为1秒。请你计算一下机器人完成任务所需的最少时间。
输入输出格式
输入格式:
输入的第一行为两个正整数N,M(N,M<=50),下面N行是储藏室的构造,0表示无障碍,1表示有障碍,数字之间用一个空格隔开。接着一行有四个整数和一个大写字母,分别为起始点和目标点左上角网格的行与列,起始时的面对方向(东E,南S,西W,北N),数与数,数与字母之间均用一个空格隔开。终点的面向方向是任意的。
输出格式:
一个整数,表示机器人完成任务所需的最少时间。如果无法到达,输出-1。
输入输出样例
输入样例#1:
9 10 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 7 2 2 7 S
输出样例#1:
12
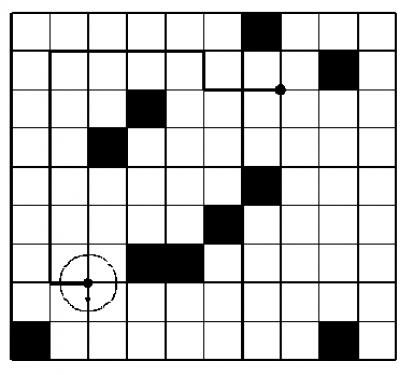
分析:机器人中心总在格点上,这也就是它走动时的中心是格点,而不是格子。我们可以将所有的格子化成点,一个格子化成四个点,
黑点优先。黑点优先是什么意思、?因为一个点化成四个点,那也就是需要 n*4,m*4个格子,但我们不用这么多,
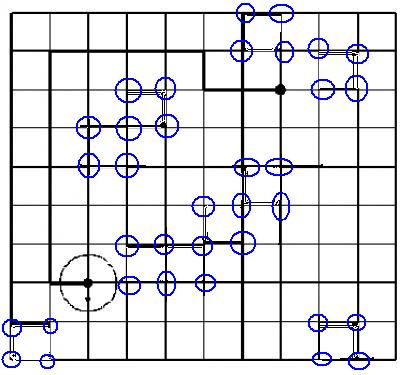
其实n+1,m+1 个格子就可以了。怎么变呢,我们让黑点的化成四个黑点,其他的不变就可以了,题目中的样例处理完厚实这样(看下图,不大好看)

这样我们会发现,只要让机器人考虑机器人的中心就可以了,机器人中心不能到最外圈的格点,机器人的中心不能走黑点,其他的可以都不用考虑。
然后广搜就可以。
注意:要cin读入字符,(为什么不能 scanf("%d%d%d%d%c",&sx,&sy,&ex,&ey,&ch);读空格吗?样例都过了,还是60分。。)
1 #include<cstdio> 2 #include<algorithm> 3 #include<queue> 4 #include<iostream> 5 6 using namespace std; 7 const int N = 55; 8 9 struct node{ 10 int x,y,step; 11 int to; 12 }cur,nxt; 13 queue<node>q; 14 int a[N][N]; 15 int mp[N][N]; 16 int dx[4]={0,1,0,-1}; //东南西北 17 int dy[4]={1,0,-1,0}; 18 bool v[N][N][5]; 19 int n,m,k,sx,sy,ex,ey; 20 char ch; 21 22 void init() 23 { 24 scanf("%d%d",&n,&m); 25 for(int i=1;i<=n;++i) 26 for(int j=1;j<=m;++j) 27 scanf("%d",&a[i][j]); 28 scanf("%d%d%d%d",&sx,&sy,&ex,&ey); 29 cin>>ch; 30 sx++; sy++; ex++; ey++; 31 for(int i=1;i<=n;++i) 32 for(int j=1;j<=m;++j) 33 if(a[i][j]==1) 34 { 35 mp[i][j] = 1; 36 mp[i+1][j] = 1; 37 mp[i][j+1] = 1; 38 mp[i+1][j+1] = 1; 39 } 40 n++; m++; 41 } 42 43 void bfs() 44 { 45 if(sx==ex && sy==ey) 46 { 47 printf("0\n"); 48 return ; 49 } 50 cur.x = sx; 51 cur.y = sy; 52 cur.step = 0; 53 switch(ch) 54 { 55 case 'E': cur.to=0;break; 56 case 'S': cur.to=1;break; 57 case 'W': cur.to=2;break; 58 case 'N': cur.to=3;break; 59 } 60 q.push(cur); 61 v[sx][sy][cur.to] = true; 62 while(!q.empty()) 63 { 64 cur = q.front() ; 65 q.pop(); 66 k = cur.to; 67 for(int i=1;i<=3;++i) 68 { 69 int xx = cur.x+i*dx[k]; 70 int yy = cur.y+i*dy[k]; 71 if(xx>1 && xx<n && yy>1 && yy<m && !mp[xx][yy]) 72 { 73 if(xx==ex && yy==ey) 74 { 75 printf("%d\n",cur.step+1); 76 return; 77 } 78 if(v[xx][yy][k]) continue; 79 v[xx][yy][k]=true; 80 nxt.x = xx; 81 nxt.y = yy; 82 nxt.step = cur.step+1; 83 nxt.to = k; 84 q.push(nxt); 85 } 86 else break; 87 } 88 nxt.x = cur.x; 89 nxt.y = cur.y; 90 nxt.step = cur.step+1; 91 nxt.to = (cur.to+1)%4; 92 if(!v[nxt.x][nxt.y][nxt.to]) 93 { 94 v[nxt.x][nxt.y][nxt.to] = true; 95 q.push(nxt); 96 } 97 nxt.to = (cur.to-1+4)%4; 98 if(!v[nxt.x][nxt.y][nxt.to]) 99 { 100 v[nxt.x][nxt.y][nxt.to] = true; 101 q.push(nxt); 102 } 103 } 104 printf("-1\n"); 105 } 106 107 int main() 108 { 109 init(); 110 bfs(); 111 return 0; 112 }

