2194: 快速傅立叶之二

2194: 快速傅立叶之二

链接

分析：

　　把相乘的，列到纸上，看一看就明白了。

k为0的情况：

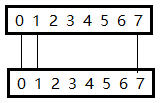
k为1的情况，7没有与它相连的点的了，于是可以加倍a数组。

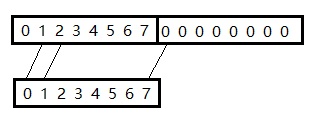
其他的同理，然后怎么快速求出这些位置的乘积之和。

将a数组翻转然后就是一个卷积的形式了，于是可以FFT。b数组后面填0即可。

 

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<cctype>
#include<set>
#include<queue>
#include<vector>
#include<map>
using namespace std;
typedef long long LL;

inline int read() {
    int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
    for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f;
}

const int N = 270005;
const double eps = 1e-10, Pi = acos(-1.0);
struct Com{
    double x, y; 
    Com(double _x = 0,double _y = 0) { x = _x, y = _y; }
}a[N], b[N];
Com operator + (const Com &A,const Com &B) { return Com(A.x + B.x, A.y + B.y); }
Com operator - (const Com &A,const Com &B) { return Com(A.x - B.x, A.y - B.y); }
Com operator * (const Com &A,const Com &B) { return Com(A.x * B.x - A.y * B.y, A.x * B.y + A.y * B.x); }

int x[N], y[N], f[N], rev[N];

void FFT(Com *a,int len,int ty) {
    for (int i = 0; i < len; ++i) if (i < rev[i]) swap(a[i], a[rev[i]]);
    Com w1, w, u, t;
    for (int m = 2; m <= len; m <<= 1) {
        w1 = Com(cos(2 * Pi / m), ty * sin(2 * Pi / m));
        for (int i = 0; i < len; i += m) {
            w = Com(1, 0);
            for (int k = 0; k < (m >> 1); ++k) {
                u = a[i + k], t = w * a[i + k + (m >> 1)];
                a[i + k] = u + t, a[i + k + (m >> 1)] = u - t;
                w = w * w1;
            }
        }
    }
}
void mul(Com *a,Com *b,int len) {
    FFT(a, len, 1);
    FFT(b, len, 1);
    for (int i = 0; i < len; ++i) a[i] = a[i] * b[i];
    FFT(a, len, -1);
    for (int i = 1; i < len; ++i) f[i] = (int)(a[i].x / (double)len + 0.5);
}
int main() {
    int n = read();
    for (int i = 0; i < n; ++i) x[i] = read(), y[i] = read();
    reverse(x, x + n + n);
    for (int i = 0; i < n + n; ++i) a[i] = Com(x[i], 0);
    for (int i = 0; i < n; ++i) b[i] = Com(y[i], 0);    
    int len = 1, lg = 0;
    while (len < n + n) len <<= 1, lg ++;
    for (int i = 0; i < len; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (lg - 1));
    mul(a, b, len);
    for (int i = n + n - 1; i > n - 1; --i) printf("%d\n", f[i]);
    return 0;
}