后缀自动机·小记
Suffix Automaton
简要记一下关于后缀自动机的知识。
Pre knowledge
有限状态自动机:功能是识别字符串,令一个自动机A,若它能识别字符串S,就记为A(S)=True,否则A(S)=False。
组成:alpha:字符集,state:状态集合,init:初始状态,end:结束状态集合,trans:状态转移函数。
后缀自动机:一个字符串S的后缀自动机,是一个能够识别S的所有后缀的自动机。
性质
1、对于一个子串,它在S中出现的结尾的位置是$R_1,R_2...R3$,叫Right集合。
2、后缀自动机上一个点有一个状态,每个状态是一个Right的集合,每个点还有26个转移,表示当前状态加入一个字符后到的状态。
3、如果存在一个子串A的Right集合是包含另一个子串B的Right集合,那么在A是B的后缀。
4、如果后缀自动机上一个点x的Right集合包含另一个点y的Right集合,那么parent树上,x是y的祖先。
5、parent树上每个父节点的Right集合都是所有子节点的Right集合的并集。
6、每个点对应的串是从根节点出发,到这个点的所构成的所有的串,最长的是Max,最短的是Min,这串的Right集合都是这个点的Right集合。设len[i]=Max(i),那么Min(i)=len[fa[i]]+1
构造
增量法构造,复杂度$O(n)$
由长度为L的后缀自动机变为长度为L+1的后缀自动机,原字符串是S,加入字符c,Right集合为{L}的设为Last,新增点为NP。
1、增加一个点后,首先会让以前所有的后缀变长,会增加一个长度为1的后缀。
2、考虑trans如何变化:Last会有一个trans为c的转移,指向NP,由于Last在parent树的祖先都是P的后缀,那么这些祖先都会有trans为c的转移。
3、考虑构建新的parent有什么变化:设P为Last的祖先,并且P在加入当前点之前,就已经有trans为c的转移了。
如果这样的P不存在,那么fa[NP]=Root,即加入c后,出了NP,没有节点的状态包含S。
否则,设Q=trans[P][c],那么Q的状态时包含S的(当然不只有S的状态)。
此时,Q代表的串中,一定有一个长度为len[P]+1的串,并且这个串是P所代表的串+x,考虑Q能否成为NP的fa。
Q所能代表的字符串可能有多个,最长的是len[Q],如果len[Q]!=len[P]+1,说明它对应的串长度在len[P]+1的串上,还长,那么说明不包含NP的Right集合。否则说明包含。
所以若len[Q]=len[P]+1,那么fa[NP]=Q。
否则:新建一个点,让它的状态既包含Q,也包含NP。
举个例子:aabab的构造,在aaba的SAM上加入b。左图为aaba的SAM,右图为aabab的SAM。
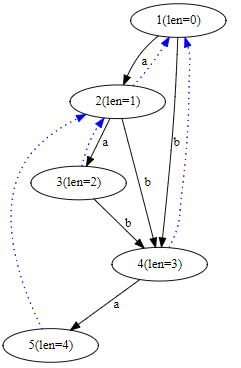
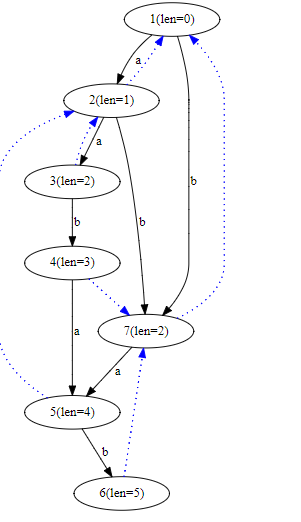
应用
1、求本质不同的子串
每个点表示的状态都不同,每个点表示的串的长度区间为Min(s)~Max(s),把所有点的Max(s)-Min(s)+1加起来即可。
2、求两个串的最长公共子串
对一个串建立SAM,扫一遍另一个串,并在第一个串的SAM跑,如果失配,沿着parent树跳。跳到一个点后,为了让答案尽量大,所以可以取这个点表示的最长的串,即len+1,然后继续跑。
3、求一个串的出现次数
找到表示这个串的状态,right集合的大小就是答案。如果在跑SAM中失配了,那么不存在这个串。
4、求第k大的子串
SAM是转移数组是一个DAG,其中从1到任一点的路径,包含了所有子串。倒序拓扑出每个点可以走出多少个点,然后从1走,走到一个点的时候判一下。
5、动态在末尾加入一个串,询问一个串的出现次数
动态加入末尾的串即可,lct维护parent树,维护每个点的right集合大小。
参考资料:
陈立杰后缀自动机课件


