4558: [JLoi2016]方
4558: [JLoi2016]方
https://lydsy.com/JudgeOnline/problem.php?id=4558
分析:
容斥原理+各种神奇的计数。
如果没有被删除了的点的话,直接计算就好了。
统计出所有的竖直放置的正方形,然后每个正方形里包含其边长个数正方形。

设外边的正方形边长为a,公式就是$(n - a + 1) \times (m - a + 1) * a$,所以可以O(n)求出。
考虑减不合法的正方形。那么分为包含一个“坏点”,2个,3个,4个。
234的时候都可以直接枚举两个点,然后就可以确定出其他的两个点了,(这里可以确定两个点后,把所有枚举到的都加上,最后除以计算了多少次。三个的可以分别枚举三条边的时候都算上,所以除以3;4个点枚举边和对角线都算上了,所以除以6)。1个的最难算。
我们把一个点面向的四个方向分开计算,因为这是一个一样的过程。
可以知道,如果确定了一个点,和一个正方形(这个点在正方形的边上),那么就会确定唯一的一个以这个点为顶点的正方形

那么我们只需要计算有多少个正方形的边上有这个点就行了,
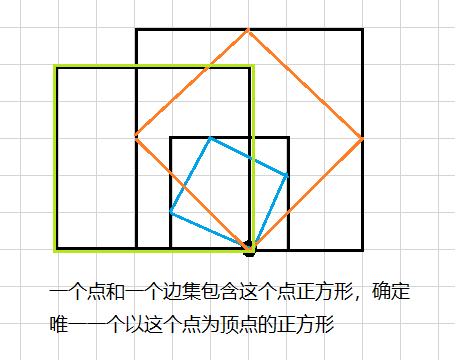
如果没有左边和右边的限制的话:
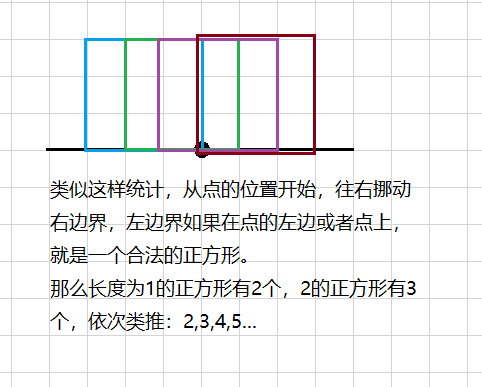
如上图,左边和右边长度都为4,先不管是否超出边界,那么就是2,3,4...8,9,分别表示长度为1,2,3...7,8的正方形。就是$\frac{n \times (n+3)}{2}$。
加上边界h的限制,正方形的边长最大为h。加上左右边界的限制,正方形的最大边长为$min(l+r,h)$,设为$z$。
这样算出来,可能是有不合法的,左边界超出了,或者右边界超出了。

于是根据等差序列求和公式,可以直接算了。
还有一点,计算这些正方形的时候,超四个方向的和加起来,会重复计算一部分。
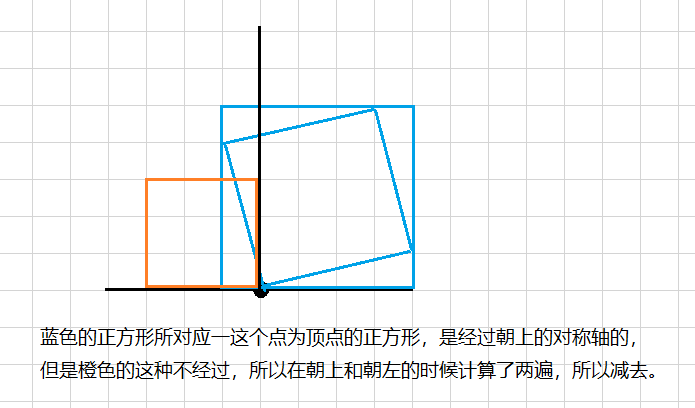
最后根据容斥原理,算出来就行了。
代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<iostream> 5 #include<cmath> 6 #include<cctype> 7 #include<set> 8 #include<queue> 9 #include<vector> 10 #include<map> 11 using namespace std; 12 typedef long long LL; 13 14 inline int read() { 15 int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; 16 for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f; 17 } 18 19 const int N = 2005; 20 const int mod = 1e8 + 7; 21 22 struct Point{ 23 int x, y; 24 Point() {} 25 Point(int _x,int _y) { x = _x, y = _y; } 26 }A[N]; 27 int n, m; 28 LL ans, t1, t2, t3, t4; 29 set<LL> s; 30 31 LL Count1(int l,int r,int h) { 32 int z = min(l + r, h); 33 if (z == 0) return 0; 34 LL ans = 1ll * z * (z + 3) / 2; 35 if (z > l) ans -= 1ll * (z - l) * (z - l + 1) / 2; 36 if (z > r) ans -= 1ll * (z - r) * (z - r + 1) / 2; 37 return (ans + mod) % mod; 38 } 39 LL Calc1(int x,int y) { // 统计一个点可以作为多少个正方形的顶点。 40 int u = x, d = n - x, l = y, r = m - y; 41 LL ans = Count1(l, r, u) + Count1(l, r, d) + Count1(u, d, l) + Count1(u, d, r); ans %= mod; 42 ans = ans - min(u, l) - min(u, r) - min(d, l) - min(d, r); 43 return (ans + mod) % mod; 44 } 45 bool inmap(Point P) { 46 return (P.x >= 0 && P.x <= n && P.y >= 0 && P.y <= m); 47 } 48 void Calc234(Point P,Point Q) { 49 if (!inmap(P) || !inmap(Q)) return ; 50 int t = s.count(1ll * P.x * (m + 1) + P.y) + s.count(1ll * Q.x * (m + 1) + Q.y); 51 ++ t2; 52 if (t >= 1) t3 ++; 53 if (t >= 2) t3 ++, t4 ++; 54 } 55 int main() { 56 n = read(), m = read();int k = read(); 57 for (int i = 1; i <= k; ++i) { 58 A[i].x = read(), A[i].y = read(); 59 s.insert(1ll * A[i].x * (m + 1) + A[i].y); // 因为列是从0开始编号的,所以需要乘以(m+1),或者直接乘以2000000 60 } 61 for (int i = 1, lim = min(n, m); i <= lim; ++i) { 62 ans += (1ll * (n - i + 1) * (m - i + 1) % mod * i % mod); 63 if (ans >= mod) ans -= mod; 64 } 65 for (int i = 1; i <= k; ++i) { 66 t1 += Calc1(A[i].x, A[i].y); 67 if (t1 >= mod ) t1 -= mod; 68 } 69 for (int i = 1; i <= k; ++i) { 70 Point P = A[i]; 71 for (int j = i + 1; j <= k; ++j) { 72 Point Q = A[j]; 73 int dx = A[i].x - A[j].x, dy = A[i].y - A[j].y; 74 Calc234(Point(P.x + dy, P.y - dx), Point(Q.x + dy, Q.y - dx)); // 作为边的情况 75 Calc234(Point(P.x - dy, P.y + dx), Point(Q.x - dy, Q.y + dx)); 76 if ((abs(dx) + abs(dy)) & 1) continue; 77 int dx2 = (dx - dy) / 2, dy2 = (dx + dy) / 2; 78 Calc234(Point(P.x - dx2, P.y - dy2), Point(Q.x + dx2, Q.y + dy2)); // 作为对角线的情况 79 } 80 } 81 ans = ans - t1 + t2 - t3 / 3 + t4 / 6; 82 ans = (ans + mod) % mod; 83 cout << ans; 84 return 0; 85 }

