DP优化——斜率优化

斜率优化学习笔记

• 前言

    在十分懵逼的听完一上午集训课之后，狂补了一下午斜率优化，理解了，但是完全没有理解，因此写这篇博客巩固一下。
  

何为斜率优化？

在日常生活中，我们食用的状态转移方程有时会以以下形式出现

\[ y=kx+b \]

什么？你说这不是状态转移方程，这是一次函数。的确，这是一次函数，但是我们可以将一些形态的转移方程转换成这样的形式，以 \(F_{i}=\min(F_{j}+(s_{i}+i-s_{j}-j-L-1)^2)\) 举例（原题：玩具装箱）。

设

\[ a_{i}=s_{i}+i\\ b_{i}=s_{i}+i+L+1 \]

得

\[\begin{split} F_{i}&=\min(F_{j}+(a_{i}-b_{j})^2)\\ F_{i}&=\min(F_{j}+a_{i}^2+b_{j}^2-2a_{i}b_{j}) \end{split} \]

我们先不考虑最小化的要求，单纯来看这个式子

\[ F_{i}=F_{j}+a_{i}^2+b_{j}^2-2a_{i}b_{j} \]

我们将有只有 \(i\) 的项看为 \(b\)；将只有 \(j\) 项看作\(y\)；将 \(i\)、\(j\) 混合的项中的常数和 \(i\) 项看作 \(k\)，\(j\) 项看作 \(x\)。

设

\[ y=F_{j}+b_{j}^2\\ k=2a_{i}\\ x=b_{j}\\ b=F_{i}-a_{i}^2 \]

欸，带入一下我们就能发现熟悉的东西

\[ F_{i}-a_{i}^2=F_{j}+b_{j}^2-2a_{i}b_{j}\\ b=y-kx \]

那有人就要说了，你这不是强加因果吗。咦，此言差矣，这个解释起来很简单，由于在枚举 \(j\)，所以只与 \(i\) 有关的变量我们当作定值（一会再说 \(F_{i}\) 的事），而只与 \(j\) 有关的我们就当作因变量，同理， \(i\)、\(j\) 混合的项就是 \(kx\)。我们现在的目标是最小化 \(F_{i}\)，而且 \(a_{i}^2\) 是我们已知的，所以转化到一次函数上，我们要最小化的就是纵截距 \(b\)。

在转换完问题后，我们看看这个一次函数有什么性质。很明显，这是条直线（废话），并且可以上下平移（改变纵截距大小），既然要最小化纵截距，那就要尽可能地使直线靠下，为了找到这样的合法情况，我们可以考虑维护一个包含所有合法状态的下凸包。

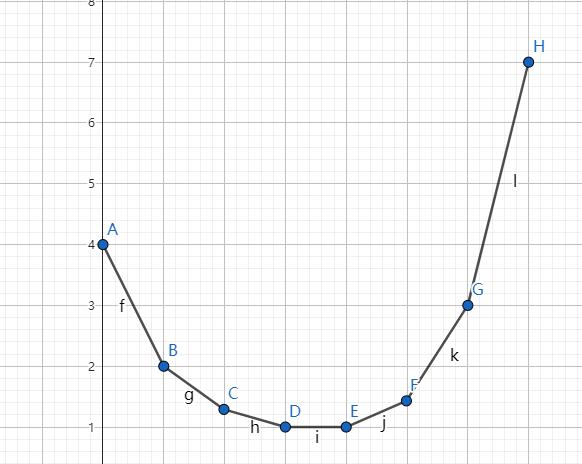
这是一个下凸包

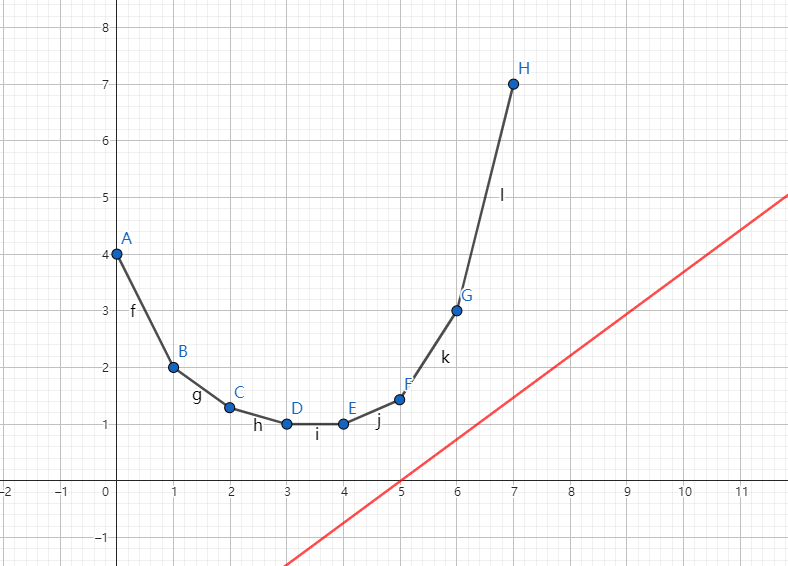
可以将红线纵截距视为我们要维护的最小值。

很明显，红线必然在凸包上，关于凸包的维护可以自行学习计算几何相关内容，这里暂时跳过，只说一下大体思路。

对于这道题，由于斜率 \(2a_{i}\) 单调递增，因此很容易用单调队列来维护凸包。在插入点之前，先判断队头的上一个节点与队头节点构成的直线斜率是否小于队头节点和要插入的节点构成的直线的斜率，由于下凸包的斜率是单调递增的，因此如果大于新插入的直线斜率的话说明上一个节点是一个上凸包，我们将队头推掉，反复进行这个过程知道不再大于，接着再将新节点插入。

咕~~~