二进制，十进制，十六进制 等 数制详解

迄今为止，所有的计算机都是以二进制形式进行算术运算和逻辑操作的，用户在键盘上输入的十进制数字和符号命令，计算机都会转成二进制的模式进行识别和运算处理，然后再把结果转换成十进制数字和符号在输出设备上面显示。

数制及其表示方式

十进制：十进制是大家熟悉的进位计数制，共有0，1，2，3，4，5，6，7，8，9这10个数字符号，这是个数字符号又称为数码。基数为10，计算时，每位逢十进一

例如：123.45 =1*10²+2*10¹+3*10⁰+4*10^-1+5*10^-2。其中，10^2，10¹，10⁰，10^-1，10^-2，称为权，整数部分中每位的幂是该位的位数减一，小数部分中每位的幂是该位的位数。

二进制：二进制是更为简单，随计算机的发展兴旺起来。有0，1这两个数码构成。基数为2。逢二进一

例如：10110.11=1*2⁴+0*2³+1*2²+1*2¹+0*2⁰+1*2^-1+1*2^-2=[22.75]_10, 

十六进制：学习和研究计算机二进制数的一中工具，共有0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F等16个数码，基数16，计算时，每位逢16进一。

例如：70F.B1=7×16²+0×16¹+F×16⁰+B×16^-l+1×16^-2=[1807.6914]₁₀,

在计算机内部，都是二进制表示，采用晶体管的导通和截至，脉冲的高电平和低电平很容易表示。运算简单，方便用于电子线路的实现。十六进制的出现可以减轻阅读和书写二进制的负担。例如：1001001111110010B=93F2H

进制数的转换

各种进制数的转换可以根据下图的方式进行转换

 

二进制转十进制

按权相加法：按权展开后相加即可

例如：10110.11=1*2⁴+0*2³+1*2²+1*2¹+0*2⁰+1*2^-1+1*2^-2=[22.75]₁₀

十进制转二进制

整数部分采用除2逆取余/乘2顺取整法：用2连续去除要转换的十进制数，直到商小于2为止。然后把各次余数最后得到的为最高位，最早得到的为最低位一次排列，所得的数就是二进制数。

例如：求215的二进制数

 

 结果是：215=11010111B (B代表二进制数)

小数部分采用乘2顺取整法：用2连续取乘要转换的十进制数，直到所得的乘积的小数部分为0或者满足所需要的精度为止，最先得到的为最高位，最后得到的为最低位依次排列。

例如：0.6879转换成二进制数

 

 结果：0.6789=0.1011B

十进制转十六进制

按权相加法：按权展开相加

例如：70F.B1=7×16²+0×16¹+F×16⁰+B×16^-l+1×16^-2=[1807.6914]₁₀,

十六进制转十进制

整数部分采用除16逆取余/乘16顺取整法：用16连续去除要转换的十进制数，直到商小于16为止。然后把各次余数最后得到的为最高位，最早得到的为最低位一次排列，所得的数就是二进制数。

例如：求3901对应的十六进制数

 

 结果：3901=D3FH（H代表16进制数）

小数部分采用乘16顺取整法：用16连续取乘要转换的十进制数，直到所得的乘积的小数部分为0或者满足所需要的精度为止，最先得到的为最高位，最后得到的为最低位依次排列。

例如：求0.76171875的十六进制数

 

结果： 0.76171875=0.C3H

二进制转十六进制

4位合一位法：从小数点开始分别向左，向右每4位一组，不足的补0，每组用十六进制表示。按序相连即可。

例如：1101111100011.10010100B 转成16进制

 

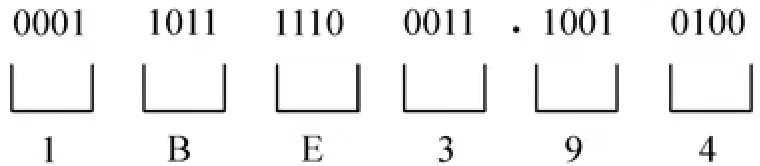
 结果：1101111100011.10010100B=1BE3.94H

十六进制转二进制

 1位拆四位法:十六进制的每位分别用二进制数码表示然后连成一体。

例如：3AB.7A5H转成二进制数

 

结果： 3AB.7A5H = 001110101011.011110100101B