Exhaustive Search

Write a program which reads a sequence A of n elements and an integer M, and outputs "yes" if you can make M by adding elements in A, otherwise "no". You can use an element only once.

You are given the sequence A and q questions where each question contains Mi.

Input

In the first line n is given. In the second line, n integers are given. In the third line q is given. Then, in the fourth line, q integers (Mi) are given.

Output

For each question Mi, print yes or no.

Constraints

• n ≤ 20
• q ≤ 200
• 1 ≤ elements in A ≤ 2000
• 1 ≤ Mi ≤ 2000

Sample Input 1

5
1 5 7 10 21
8
2 4 17 8 22 21 100 35

Sample Output 1

no
no
yes
yes
yes
yes
no
no

Notes

You can solve this problem by a Burte Force approach. Suppose solve(p, t) is a function which checkes whether you can make t by selecting elements after p-th element (inclusive). Then you can recursively call the following functions:

solve(0, M) 
solve(1, M-{sum created from elements before 1st element}) 
solve(2, M-{sum created from elements before 2nd element}) 
...

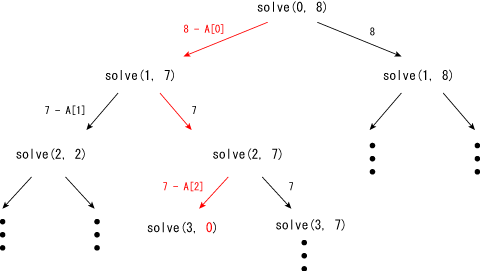
The recursive function has two choices: you selected p-th element and not. So, you can check solve(p+1, t-A[p]) and solve(p+1, t) in solve(p, t) to check the all combinations.

For example, the following figure shows that 8 can be made by A[0] + A[2].

 

#include <iostream>
using namespace std;

int n, q;
int A[2010], M[2010];

// 用第i个元素后面的元素能得出m时返回true 
// 从输入值M中减去所选元素的递归函数 
bool solve(int i, int m)
{
	if(m == 0)	return true;
	if(i >= n)	return false;
	return solve(i + 1, m) || solve(i + 1, m - A[i]);	// 不使用第i个元素 + 使用第i个元素 
}

int main()
{
	cin >> n;
	for(int i = 0; i < n; ++ i)
	{
		cin >> A[i];
	}
	cin >> q;
	for(int i = 0; i < q; ++ i)
	{
		cin >> M[i];
		if(solve(0, M[i]))
		{
			cout << "yes" << endl;
		}
		else
		{
			cout << "no" << endl;
		}
	}
	
	return 0;
}

/*
5
1 5 7 10 21
8
2 4 17 8 22 21 100 35
*/