结对编程
-
教学班级:006
-
项目地址:
-
https://github.com/Pandapan-Buaa/IntersectInPair.git
PSP 表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 880 | 1000 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 60 | 60 |
| · Design Spec | · 生成设计文档 | 60 | 120 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 60 | 60 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 40 | 40 |
| · Design | · 具体设计 | 60 | 60 |
| · Coding | · 具体编码 | 360 | 400 |
| · Code Review | · 代码复审 | 40 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 80 | 80 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 40 | 40 |
| · Size Measurement | · 计算工作量 | 20 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 60 |
| 合计 | 880 | 1000 |
Information Hiding,Interface Design,Loose Coupling
Information Hiding:对数据进行封装,让外部不能随便访问。由于本次作业的计算比较多,为了提高效率,并没有遵守这个原则,类的成员变量都被设为public。
Loose Coupling:松耦合。每个模块自身是一个整体,各个模块之间的依赖尽可能少,这样修改一个模块时,就不用修改其他的模块。我们的核心计算模块向UI模块提供了添加和删除图形的两个接口,UI模块不用考虑计算模块的具体实现,只需要调用接口函数,UI模块和计算模块之间的耦合比较低。
计算模块接口的设计与实现过程
与上次作业类似,本次作业里只有三个类(点/向量、线、圆)及其公共常用函数以及三个求解函数,在类中只需对应属性以及提供向量计算的相关函数,并在三个求解函数中对类的交点进行求解。
求解函数的关键代码如下:
其中line.isOnLine()是判断点是否在线段/射线上的简单方法,其实现则是根据直线/线段/射线的向量方程 l = u + tv ,u是直线上一点,v是方向向量,t是系数,计算出t则易判断是否在所给线上。
void lineIntersectLine(const Line& l1, const Line& l2)
{
if (dcmp(l1.v ^ l2.v) == 0) return;
Vector u = l1.p - l2.p;
double t = (l2.v ^ u) / (l1.v ^ l2.v);
Point temp = l1.p + l1.v * t;
if (l1.type != "L" && !l1.isOnLine(temp)) return;
if (l2.type != "L" && !l2.isOnLine(temp)) return;
try {
points.insert(temp);
}
catch(exception e){}
}
void lineIntersectCircle(const Line& L, const Circle& C)
{
double t1, t2;
double a = L.v.x, b = L.p.x - C.c.x, c = L.v.y, d = L.p.y - C.c.y;
double e = a * a + c * c, f = 2 * (a * b + c * d), g = b * b + d * d - C.r * C.r;
double delta = f * f - 4 * e * g;
if (dcmp(delta) < 0) return; //线圆相离
if (dcmp(delta) == 0) { //线圆相切
t1 = t2 = -f / (2 * e);
if (L.type != "L" && !L.isOnLine(t1)) return;
try {
points.insert(L.point(t1));
}
catch (exception e) {
}
return;
}
//线圆相交
t1 = (-f - sqrt(delta)) / (2 * e);
t2 = (-f + sqrt(delta)) / (2 * e);
Point p1 = L.point(t1);
Point p2 = L.point(t2);
if (L.type != "L" && !L.isOnLine(p1));
else {
try {
points.insert(p1);
}
catch (exception e) {
}
}
if (L.type != "L" && !L.isOnLine(p2));
else {
try {
points.insert(p2);
}
catch (exception e) {
}
}
return;
}
void circleIntersectCircle(const Circle& c1, const Circle& c2)
{
double d = Length(c1.c - c2.c);
if (dcmp(d) == 0) return; //两圆重合
if (dcmp(c1.r + c2.r - d) < 0) return;
if (dcmp(fabs(c1.r - c2.r) - d) > 0) return;
double a = angle(c2.c - c1.c);
double da = acos((c1.r * c1.r + d * d - c2.r * c2.r) / (2 * c1.r * d));
Point p1 = c1.point(a - da), p2 = c1.point(a + da);
try {
points.insert(p1);
}
catch (exception e) {
}
if (p1 == p2) return;
try {
points.insert(p2);
}
catch (exception e) {
}
}
独到之处在于:用计算几何的方法,简洁高效的解决了核心代码的拓展部分。
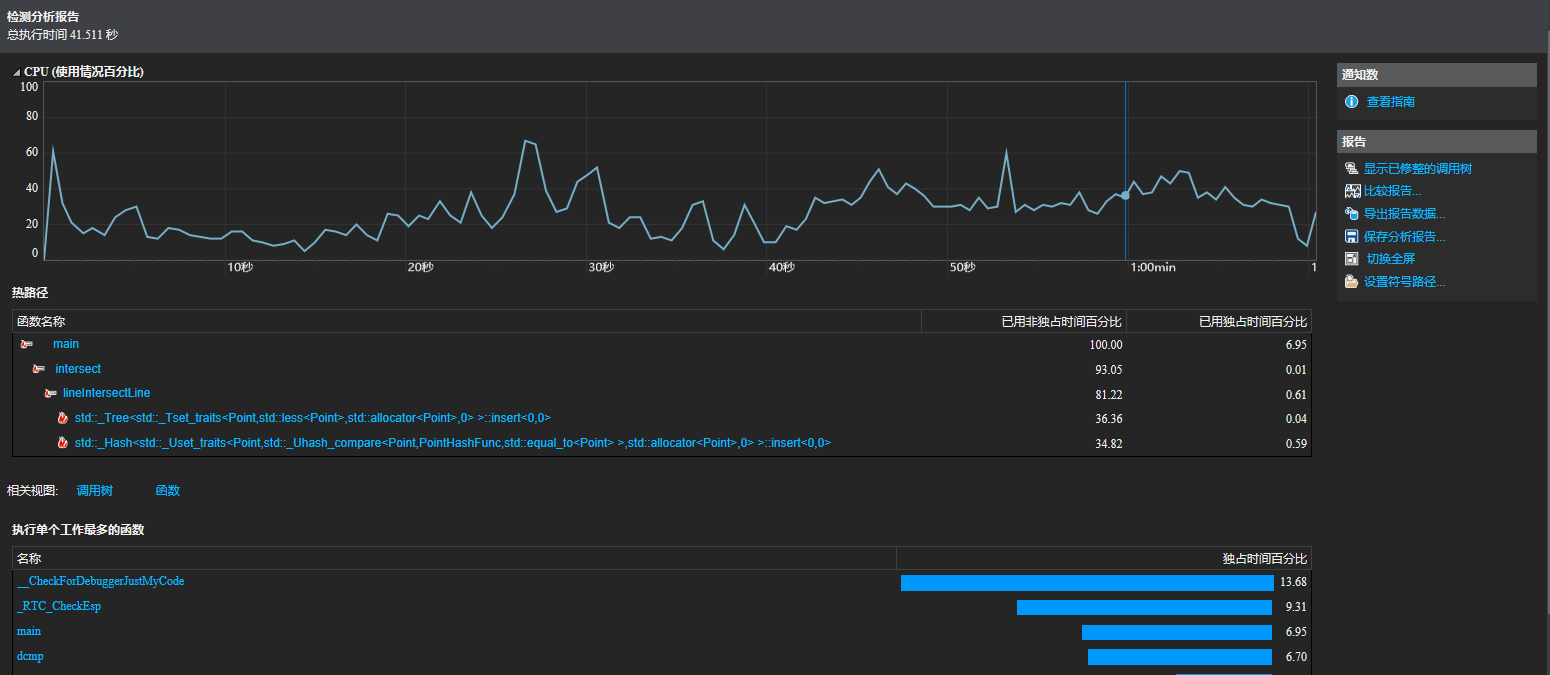
计算模块接口部分的性能改进
性能改进方面依然没有想出更优复杂度的算法,只能够进行一些细节上的优化。由于C++的set是基于红黑树实现的,插入操作的复杂度为O(logn),所以考虑了换成基于哈希表实现的unordered_set, 在哈希函数理想的情况下,插入操作的复杂度为O(1)。换了unordered_set之后性能确实有了提升,在1000条直线,400000个交点的情况下,所用时间从9秒左右提升到了6秒左右。
Design by Contract
Design by Contract就是契约式编程,在大二的面向对象课程有过了解。这种方法规定了函数的前提条件,后继条件,不变量条件等,优点是严格区分了责任,让每个人只用关心自己的代码正确性。缺点是可能会在函数各种条件的考虑上花费很多时间。
项目中并没有严格地使用契约式编程,只是规定了一些接口的作用,参数,返回值。
计算模块部分单元测试展示
在构造测试数据时,两两组合,分为L_L,R_R, S_S, L_R, L_S, L_C, R_S, R_C, S_C, C_C十种情况。
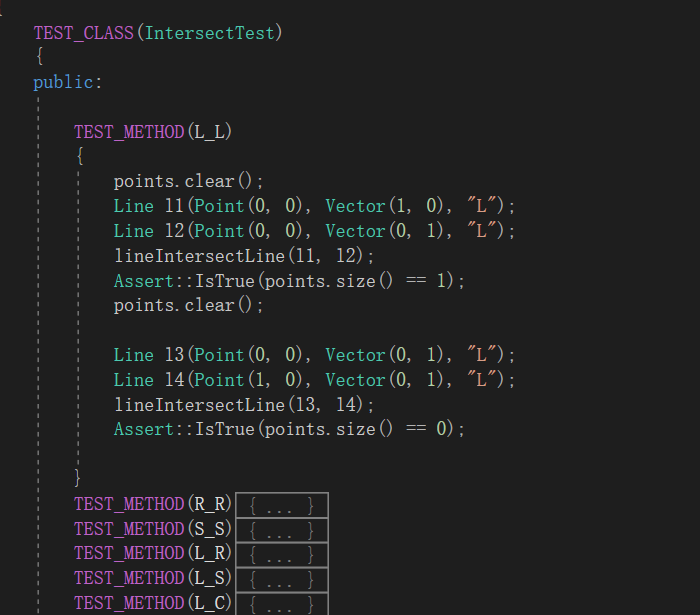
首先把能想到的情况进行了测试,比如直线相交,直线平行,射线端点,直线与圆相交,相切,相离等情况,然后根据覆盖率工具显示的未覆盖的分支,再添加对应的测试数据 。
测试覆盖率:
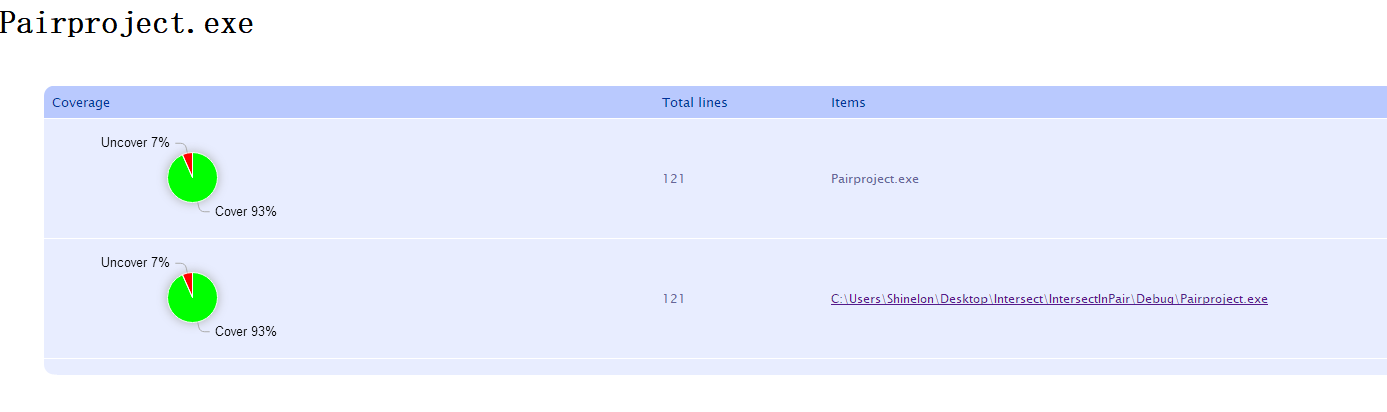
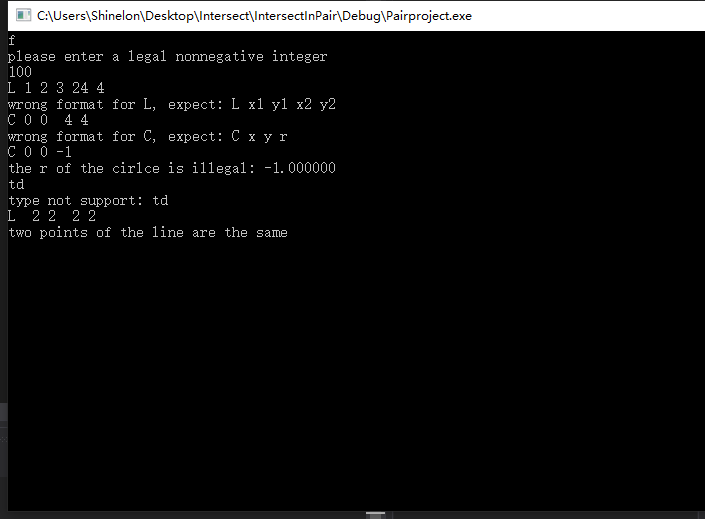
计算模块部分异常处理说明
只设计了一个异常类,定义了五种异常类型。
WRONGTYPE: 输入了L, R, S, C之外的不支持的类型。
WRONGFORMAT: 输入了不符合规范的格式。
BADPOINT: 输入的点的坐标不在(-100000,100000)范围内。
BADLINE: 输入的直线的两个端点重合。
BADCIRCLE: 输入的圆的半径r小于等于0。


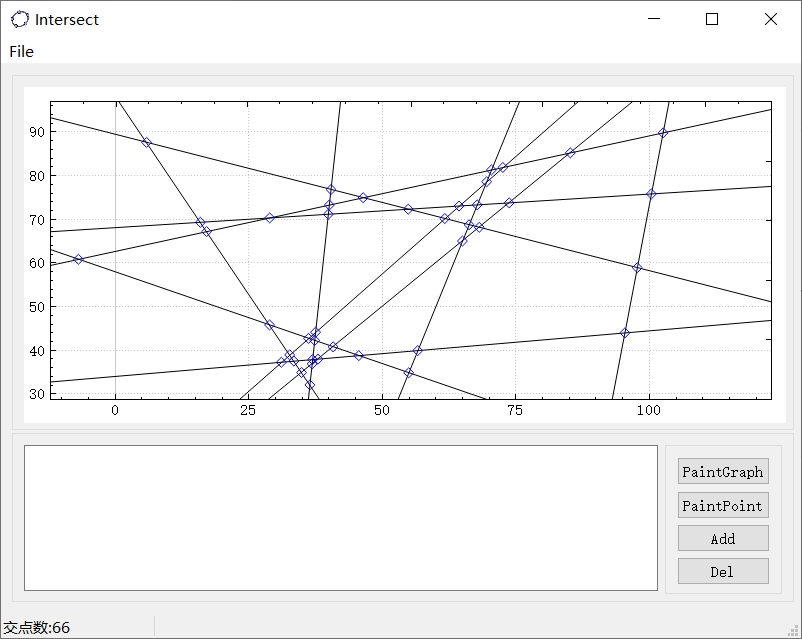
界面模块的详细设计过程
首先决定采用基于C++的QT编写UI,在资料查询的过程中,我发现了QT的第三方库QcustomPlot,看完其基本演示后,发现能够较为简单的实现类似GeoGebra的界面放缩和绘制功能,因此决定以QT+QcustomPlot完成UI任务。在阅读完《Qt5.9 c++开发指南》的前四章以及第七章IO处理之后,我认为已有的知识已经足够了,因此开始查询QcustomPlot官方文档以及答疑,同时进行UI代码编写。

UI界面如上,共有四个Button(分别负责绘制图像、交点、添加、删除,其中添加删除格式与输入格式一致,例如“L 0 0 1 1”),一条menubar(负责打开文本文件),一个TextEdit(负责显示文本文件以及输入),一个结果Lable(显示交点数目),以及QcustomPlot区域(绘图),由于QT是可以可视化拖动模块并自动对其产生代码的,所以该部分的设计实现并不是人工的。
接着为了实现上述的功能,需要利用QT中的信号与槽机制,按钮的信号在其库中已有定义,需要写的是按钮按下后的反应,即按钮对应的槽,如下:
private slots:
void on_actOpen_triggered();
void on_AddBtn_clicked();
void on_DelBtn_clicked();
void on_PaintBtn_clicked();
void on_PointBtn_clicked();
具体代码过长就不做展示了。这些槽函数定义了按钮的反应,Add和Del对应的是核心代码接口,这里主要讲两个绘制按钮的槽。
根据QcustomPlot官方文档可知其对圆,直线,射线,点均有多种不同实现方法,但大体而言分两类,一类在Graph对象中添加点集,形成图像;另一类AbstractItem则是直接对图像进行绘制(这里的原理并未细究,但其绘制速度是远超于点绘制的)。因此我编写了不同的绘制函数,如下:
void paintPoint(QCustomPlot *customPlot,double x,double y);
void paintLine(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
void paintRay(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
void paintSegment(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
void paintCircle(QCustomPlot *customPlot,double x1, double y1, double x2, double y2);
经测试,在500000数量级的绘制下均可以保持使用流畅(当然,绘制需要时间,该库还提供了Opengl加速,但我并未实验)
界面模块与计算模块的对接
由于提前设计了接口
void add_diagram(char T, int x1, int y1, int x2, int y2);
void sub_diagram(char T, int a, int b, int c, int d);
void calPoints();
set<pair<double, double>> uiPoints;
因此在对接时只需要在四个按钮对应槽中合理调用接口即可。
实现的功能:
-
支持从文件导入几何对象的描述。
左上角File处可以添加文件,并显示在下方文本框中。
-
支持几何对象的添加、删除。
按下Add,Del按钮会添加/删除文本框中的集合对象
-
支持绘制现有几何对象。
PaintGraph按钮实现
-
支持求解现有几何对象交点并绘制。
PaintPoint按钮实现
-
坐标系放缩,平移 (数量级10^-5 ~ 10^250)
结对过程
腾讯会议屏幕共享截图
日常微信交流截图

结对编程优缺点
我认为结对编程的好处在于:结对编程的两个人可以互相监督,不容易偷懒,可以互相学习编程技巧,以及可以同时检查代码,有效地减少bug。
坏处:可能会在某个问题上产生不同的想法,互相沟通会花费一些时间。
成员的优点和缺点:
我: 优点:思路清晰,比较认真
缺点:容易偷懒
对方:优点:很认真,耐心,学习能力很强
缺点:不是很细心
附加题
交换团队(17373259 、 17373250)
由于和对方团队提前商量好了接口,因此模块的替换较为容易,基本无需更改。
将DLL替换后编码如下(以添加Add按钮为例)
QString text = ui->textEdit->toPlainText();
QFile outFile("./temp.txt");
outFile.open(QIODevice::WriteOnly);
QTextStream out(&outFile);
for(int i = 0 ; i < text.size();i++){
out << text.at(i);
}
outFile.close();
QFile inFile("./temp.txt");
inFile.open(QIODevice::ReadOnly);
QTextStream in(&inFile);
QChar sub;
int x1,y1,x2,y2,r;
QCustomPlot *customPlot = ui->qcustomPlot;
while(in.atEnd() == false){
in >> sub ;
if(sub == "L") {
in >> x1 >> y1 >> x2 >> y2;
add_diagram('L',x1,y1,x2,y2);
}
else if(sub == "R"){
in >> x1 >> y1 >> x2 >> y2;
add_diagram('R',x1,y1,x2,y2);
}
else if(sub == "S"){
in >> x1 >> y1 >> x2 >> y2;
add_diagram('S',x1,y1,x2,y2);
}
else if(sub == "C"){
in >> x1 >> y1 >> r;
add_diagram('C',x1,y1,r,0);
}
}
ui->textEdit->clear();
cout << point_map.size() << endl;
基本不需要修改源代码,即可完成dll更改。
一开始由于随机生成的测试样例中存在平行直线,出现了一些问题(己方dll是在QT中重新改写生成的,并未将核心代码中的错误处理部分导入,造成了这个测试样例中的问题未被及时发现)。后续修改后,经过测试,对方dll能够完成任务需求。