AIM Tech Round 5C. Rectangles 思维

C. Rectangles

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given $\mathrm{nn rectangles\; on\; a\; plane\; with\; coordinates\; of\; their\; bottom\; left\; and\; upper\; right\; points.\; Some (n-1)(n-1) of\; the\; given nn rectangles\; have\; some\; common\; point.\; A\; point\; belongs\; to\; a\; rectangle\; if\; this\; point\; is\; strictly\; inside\; the\; rectangle\; or\; belongs\; to\; its\; boundary.}$

Find any point with integer coordinates that belongs to at least $(n-1)(n-1) given\; rectangles.$

Input

The first line contains a single integer $\mathrm{nn (2\le n\le 1326742\le n\le 132674)\; —\; the\; number\; of\; given\; rectangles.}$

Each the next $\mathrm{nn lines\; contains\; four\; integers x1x1, y1y1, x2x2 and y2y2 (-109\le x1<x2\le 109-109\le x1<x2\le 109, -109\le y1<y2\le 109-109\le y1<y2\le 109)\; —\; the\; coordinates\; of\; the\; bottom\; left\; and\; upper\; right\; corners\; of\; a\; rectangle.}$

Output

Print two integers $\mathrm{xx and yy —\; the\; coordinates\; of\; any\; point\; that\; belongs\; to\; at\; least (n-1)(n-1) given\; rectangles.}$

Examples

input

Copy

3
0 0 1 1
1 1 2 2
3 0 4 1

output

Copy

1 1

input

Copy

3
0 0 1 1
0 1 1 2
1 0 2 1

output

Copy

1 1

input

Copy

4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4

output

Copy

1 1

input

Copy

5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2

output

Copy

3 4

Note

The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.

 

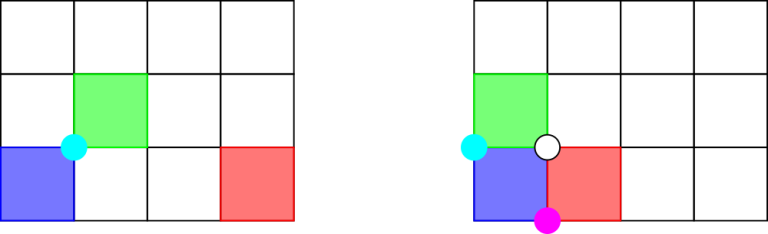
题意：给出n个矩形，找一个点至少同时在n-1个矩形内。

思路：我们分别对每条对角线求前缀交和后缀交，则若在每个条对角线左右两边的的前缀与后缀取交后还存在交点，即为解。

代码：

#include"bits/stdc++.h"

#define db double
#define ll long long
#define vl vector<ll>
#define ci(x) scanf("%d",&x)
#define cd(x) scanf("%lf",&x)
#define cl(x) scanf("%lld",&x)
#define pi(x) printf("%d\n",x)
#define pd(x) printf("%f\n",x)
#define pl(x) printf("%lld\n",x)
#define rep(i, n) for(int i=0;i<n;i++)
using namespace std;
const int N = 1e6 + 5;
const int mod = 1e9 + 7;
const int MOD = 998244353;
const db  PI = acos(-1.0);
const db  eps = 1e-10;
const ll  INF = 0x3fffffffffffffff;
int n;
struct P{
    int d,l,u,r;
    inline P operator | (P a){
        return (P){max(a.d,d),max(a.l,l),min(a.u,u),min(a.r,r)};
    }
}a[N],pre[N],suf[N];
int main(){
    ci(n);
    for(int i=1;i<=n;i++){
       ci(a[i].d),ci(a[i].l),ci(a[i].u),ci(a[i].r);
    }
    pre[0]=suf[n+1]={-mod,-mod,mod,mod};//初始化
    for(int i=1;i<=n;i++){
        pre[i]=pre[i-1]|a[i];//前缀
    }
    for(int i=n;i>=1;i--){
        suf[i]=suf[i+1]|a[i];//后缀
    }
    for(int i=1;i<=n;i++){
        P tmp=pre[i-1]|suf[i+1];//取交
        if(tmp.d<=tmp.u&&tmp.l<=tmp.r) return !printf("%d %d\n",tmp.d,tmp.l);
    }
    return 0;
}