Codeforces Round #460 (Div. 2).E 费马小定理+中国剩余定理

E. Congruence Equation
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Given an integer x. Your task is to find out how many positive integers n (1 ≤ n ≤ x) satisfy

where a, b, p are all known constants.
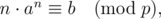
Input

The only line contains four integers a, b, p, x (2 ≤ p ≤ 106 + 3, 1 ≤ a, b < p, 1 ≤ x ≤ 1012). It is guaranteed that p is a prime.

Output

Print a single integer: the number of possible answers n.

Examples
input
2 3 5 8
output
2
input
4 6 7 13
output
1
input
233 233 10007 1
output
1
Note

In the first sample, we can see that n = 2 and n = 8 are possible answers.

题意：给出a, b, p, x，求有多少个n满足:n*a^n%p==b(n<=x)

思路：先要知道一个很简单的性质：a^n%p=(a%p)^(n%p-1)%p=a^(n%p-1),即a^n仅有p-1种结果。

①暴力枚举a^i%p (i从0到p-1)算出每个余数，可以得到式子n*a^i%p==b

②对于每个a^i，用逆元求出c，n%p = c= b*inv(a^i)%p

③则n%(p-1)==i 且n%p==c，最小的n可以用CRT求出，n的周期是P=p*(p-1).

代码：

 1 //#include "bits/stdc++.h"
 2 #include "cstdio"
 3 #include "map"
 4 #include "set"
 5 #include "cmath"
 6 #include "queue"
 7 #include "vector"
 8 #include "string"
 9 #include "cstring"
10 #include "time.h"
11 #include "iostream"
12 #include "stdlib.h"
13 #include "algorithm"
14 #define db double
15 #define ll long long
16 //#define vec vector<ll>
17 #define Mt  vector<vec>
18 #define ci(x) scanf("%d",&x)
19 #define cd(x) scanf("%lf",&x)
20 #define cl(x) scanf("%lld",&x)
21 #define pi(x) printf("%d\n",x)
22 #define pd(x) printf("%f\n",x)
23 #define pl(x) printf("%lld\n",x)
24 #define inf 0x3f3f3f3f
25 #define rep(i, x, y) for(int i=x;i<=y;i++)
26 const int N   = 1e6 + 5;
27 const int mod = 1e9 + 7;
28 const int MOD = mod - 1;
29 const db  eps = 1e-10;
30 const db  PI  = acos(-1.0);
31 using namespace std;
32 ll a,b,p,x;
33 ll m[2],f[2];
34 ll exgcd(ll a, ll b, ll &x, ll &y)
35 {
36     ll d;
37     //if (a == 0 && b == 0) return -1;
38     if (b == 0)
39     {
40         x = 1;
41         y = 0;
42         return a;
43     }
44     d = exgcd(b, a%b, y, x);
45     y -= a / b * x;
46     return d;
47 }
48 
49 ll inv(ll a, ll MOD)
50 {
51     ll x, y, d;
52     d = exgcd(a, MOD, x, y);
53     if (d == 1)
54         return (x % MOD + MOD) % MOD;
55     // else   return -1;
56 }
57 ll china(ll *f, ll *m){
58     ll M = 1, ret = 0;
59     for(int i = 0; i < 2; i ++) M *= m[i];
60     for(int i = 0; i < 2; i ++){
61         ll w = M / m[i];
62         ret = (ret + w * inv(w, m[i]) * f[i]) % M;
63     }
64     return (ret + M) % M;
65 }
66 ll qpow(ll x,ll n)
67 {
68     ll ans=1;
69     x%=p;
70     while(n){
71         if(n&1) ans=ans*x%p;
72         x=x*x%p;
73         n>>=1;
74     }
75     return  ans;
76 }
77 
78 int main()
79 {
80     cl(a),cl(b),cl(p),cl(x);
81     a%=p;
82     ll ans=0,P=p*(p-1);
83     m[0]=p-1,m[1]=p;
84     for(int i=0;i<p-1;i++)
85     {
86         f[0]=i;
87         f[1]=inv(qpow(a,i),p)*b%p;
88         ll xx=china(f,m);
89         ans+=(x-xx+P)/P;
90     }
91     pl(ans);
92     return 0;
93 }

 

 

posted @ 2018-02-01 23:34  thges  阅读(207)  评论(0)  编辑  收藏  举报