893E - Counting Arrays

E. Counting Arrays
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

You are given two positive integer numbers x and y. An array F is called an y-factorization of x iff the following conditions are met:

  • There are y elements in F, and all of them are integer numbers;
  • .

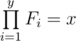You have to count the number of pairwise distinct arrays that are y-factorizations of x. Two arrays A and B are considered different iff there exists at least one index i (1 ≤ i ≤ y) such that Ai ≠ Bi. Since the answer can be very large, print it modulo 109 + 7.

Input

The first line contains one integer q (1 ≤ q ≤ 105) — the number of testcases to solve.

Then q lines follow, each containing two integers xi and yi (1 ≤ xi, yi ≤ 106). Each of these lines represents a testcase.

Output

Print q integers. i-th integer has to be equal to the number of yi-factorizations of xi modulo 109 + 7.

Example
input
2
6 3
4 2
output
36
6
Note

In the second testcase of the example there are six y-factorizations:

  • { - 4,  - 1};
  • { - 2,  - 2};
  • { - 1,  - 4};
  • {1, 4};
  • {2, 2};
  • {4, 1}.

题意：给出x,y。求满足含有y个元素的之积是x的数列个数。

思路：排列组合，插空法。

代码：

 1 #include<bits/stdc++.h>
 2 #define db double
 3 #define ll long long
 4 #define vec vector<ll>
 5 #define Mt  vector<vec>
 6 #define ci(x) scanf("%d",&x)
 7 #define cd(x) scanf("%lf",&x)
 8 #define cl(x) scanf("%lld",&x)
 9 #define pi(x) printf("%d\n",x)
10 #define pd(x) printf("%f\n",x)
11 #define pl(x) printf("%lld\n",x)
12 #define rep(i,x,y) for(int i=x;i<=y;i++)
13 #define debug puts("-------------");
14 const int N = 1e6 + 2015;
15 const int mod = 1e9 + 7;
16 const int MOD = mod-1;
17 const db  eps = 1e-18;
18 const db  PI = acos(-1.0);
19 using namespace std;
20 bool v[N];
21 int pri[N];
22 ll F[N], Finv[N], inv[N];//F是阶乘，Finv是逆元的阶乘
23 
24 int p=0;
25 void init()
26 {
27     memset(v,0,sizeof(v));
28     for(int i=2;i<1002002;i++){
29         if(!v[i]) pri[p++]=i;
30         for(int j=2*i;j<1002002;j+=i) {v[j]=1;}
31     }
32     inv[1] = 1;
33     for(int i = 2; i < 1002005; i ++){
34         inv[i] = (mod - mod / i) * 1ll * inv[mod % i] % mod;
35     }
36     F[0] = Finv[0] = 1;
37     for(int i = 1; i < 1002005; i ++){
38         F[i] = F[i-1] * 1ll * i % mod;
39         Finv[i] = Finv[i-1] * 1ll* inv[i] % mod;
40     }
41 }
42 ll C(ll n, ll m){    //comb(n, m)就是C(n, m)
43     if(m < 0 || m > n)  return 0;
44     return F[n] * 1ll * Finv[n - m] % mod * Finv[m] % mod;
45 }
46 ll qpow(ll x,ll n)
47 {
48     ll ans=1;
49     x%=mod;
50     while(n){
51         if(n&1) ans=ans*x%mod;
52         x=x*x%mod;
53         n>>=1;
54     }
55     return  ans;
56 }
57 
58 int main(){
59     int q;
60     ci(q);
61     init();
62     for(int i=0;i<q;i++)
63     {
64         ll x,y;
65         cl(x),cl(y);
66         ll ans=qpow(2,y-1);
67         if(x==1){
68             pl(qpow(2, y - 1));
69             continue;
70         }
71         vector<int> e;e.clear();
72         map<int,int> mp;mp.clear();
73         int id=0;
74         while(x>1){
75             if(x%pri[id]==0){
76                 int n=0;
77                 while(x%pri[id]==0) n++,x/=pri[id];
78                 ans=ans*C(n+y-1,y-1)%mod;
79             }
80             id++;
81             if(pri[id]>1000){
82                 if(x>1) ans=ans*y%mod;
83                 break;
84             }
85         }
86         pl(ans);
87     }
88     return 0;
89 }

 

posted @ 2017-11-28 23:13  thges  阅读(259)  评论(0)  编辑  收藏  举报