胜者树与败者树

胜者树与败者树  

 

       胜者树和败者树都是完全二叉树，是树形选择排序的一种变型。每个叶子结点相当于一个选手，每个中间结点相当于一场比赛，每一层相当于一轮比赛。

 

      不同的是，胜者树的中间结点记录的是胜者的标号；而败者树的中间结点记录的败者的标号。

 

       胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后，利用中间结点的信息，还是能够快速地找到最值。在k路归并排序中经常用到。

 

一、胜者树

      

       胜者树的一个优点是，如果一个选手的值改变了，可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树，而不必改变其他比赛的结果。

 

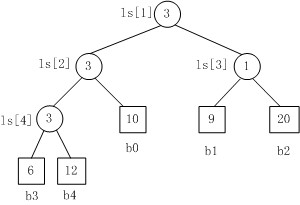
Fig. 1

Fig.1是一个胜者树的示例。规定数值小者胜。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；

2.         b3 PK b0，b3胜b0负，内部结点ls[2]的值为3；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；

4.         b3 PK b1，b3胜b1负，内部结点ls[1]的值为3。.

当Fig. 1中叶子结点b3的值变为11时，重构的胜者树如Fig. 2所示。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；

2.         b3 PK b0，b0胜b3负，内部结点ls[2]的值为0；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；

4.         b0 PK b1，b1胜b0负，内部结点ls[1]的值为1。.

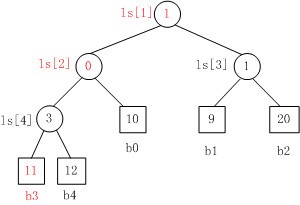
Fig. 2

 

 

二、败者树

 

       败者树是胜者树的一种变体。在败者树中，用父结点记录其左右子结点进行比赛的败者，而让胜者参加下一轮的比赛。败者树的根结点记录的是败者，需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。

 

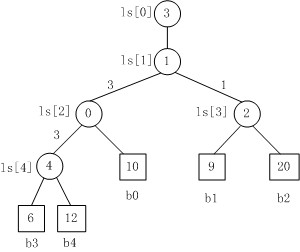
Fig. 3

Fig. 3是一棵败者树。规定数大者败。

1.         b3 PK b4，b3胜b4负，内部结点ls[4]的值为4；

2.         b3 PK b0，b3胜b0负，内部结点ls[2]的值为0；

3.         b1 PK b2，b1胜b2负，内部结点ls[3]的值为2；

4.         b3 PK b1，b3胜b1负，内部结点ls[1]的值为1；

5.         在根结点ls[1]上又加了一个结点ls[0]=3，记录的最后的胜者。

败者树重构过程如下：

·            将新进入选择树的结点与其父结点进行比赛：将败者存放在父结点中；而胜者再与上一级的父结点比较。

·            比赛沿着到根结点的路径不断进行，直到ls[1]处。把败者存放在结点ls[1]中，胜者存放在ls[0]中。

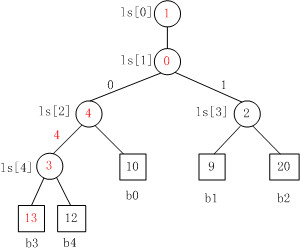
Fig. 4

       Fig. 4是当b3变为13时，败者树的重构图。

 

       注意，败者树的重构跟胜者树是不一样的，败者树的重构只需要与其父结点比较。对照Fig. 3来看，b3与结点ls[4]的原值比较，ls[4]中存放的原值是结点4，即b3与b4比较，b3负b4胜，则修改ls[4]的值为结点3。同理，以此类推，沿着根结点不断比赛，直至结束。

 

        由上可知，败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关，而胜者树的重构还与该结点的兄弟结点有关。

 

 

 

败者树 多路平衡归并外部排序

 

 

 

 

一 外部排序的基本思路

假设有一个72KB的文件，其中存储了18K个整数，磁盘中物理块的大小为4KB，将文件分成18组，每组刚好4KB。

首先通过18次内部排序，把18组数据排好序，得到初始的18个归并段R1~R18，每个归并段有1024个整数。

然后对这18个归并段使用4路平衡归并排序：

第1次归并：产生5个归并段

R11   R12    R13    R14    R15

其中

R11是由{R1,R2,R3,R4}中的数据合并而来

R12是由{R5,R6,R7,R8}中的数据合并而来

R13是由{R9,R10,R11,R12}中的数据合并而来

R14是由{R13,R14,R15,R16}中的数据合并而来

R15是由{R17,R18}中的数据合并而来

把这5个归并段的数据写入5个文件：

foo_1.dat    foo_2.dat    foo_3.dat     foo_4.dat     foo_5.dat

 

第2次归并：从第1次归并产生的5个文件中读取数据，合并，产生2个归并段

R21  R22

其中R21是由{R11,R12,R13,R14}中的数据合并而来

其中R22是由{R15}中的数据合并而来

把这2个归并段写入2个文件

bar_1.dat   bar_2.dat

 

第3次归并：从第2次归并产生的2个文件中读取数据，合并，产生1个归并段

R31

R31是由{R21,R22}中的数据合并而来

把这个文件写入1个文件

foo_1.dat

此即为最终排序好的文件。

 

二 使用败者树加快合并排序

外部排序最耗时间的操作时磁盘读写，对于有m个初始归并段，k路平衡的归并排序，磁盘读写次数为

|logkm|，可见增大k的值可以减少磁盘读写的次数，但增大k的值也会带来负面效应，即进行k路合并

的时候会增加算法复杂度，来看一个例子。

把n个整数分成k组，每组整数都已排序好，现在要把k组数据合并成1组排好序的整数，求算法复杂度

u1: xxxxxxxx

u2: xxxxxxxx

u3: xxxxxxxx

.......

uk: xxxxxxxx

算法的步骤是：每次从k个组中的首元素中选一个最小的数，加入到新组，这样每次都要比较k-1次，故

算法复杂度为O((n-1)*(k-1))，而如果使用败者树，可以在O(logk)的复杂度下得到最小的数，算法复杂

度将为O((n-1)*logk)， 对于外部排序这种数据量超大的排序来说，这是一个不小的提高。

 

关于败者树的创建和调整，可以参考清华大学《数据结构-C语言版》

 

转：http://blog.csdn.net/whz_zb/article/details/7425152

 

关于败者树和K路归并：

每一路都相当于败者树的叶子节点，每次把胜者pop出，然后从对应的路中取得新的节点，然后进行败者树的重构，每次的重构复杂度是O(logk)。