常用算法模板(参考AcWing、0x3f)
1.基础算法
快速排序
// 以中心点
void quickSort(vector<int>& nums, int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = nums[l + r >> 1];
while (i < j)
{
do i ++ ; while (nums[i] < x);
do j -- ; while (nums[j] > x);
if (i < j) swap(nums[i], nums[j]);
}
quickSort(nums, l, j);
quickSort(nums, j + 1, r);
}
// 以左端点
void quickSort(vector<int>& nums, int l, int r)
{
if (l >= r) return;
int i = l, j = r, x = nums[l];
while (i < j)
{
// 先右到左
while (i < j && nums[j] >= x) --j;
// 再左到右
while (i < j && nums[i] <= x) ++i;
if (i < j) swap(nums[i], nums[j]);
}
swap(nums[i], nums[l]);
quickSort(nums, l, i - 1);
quickSort(nums, i + 1, r);
}
归并排序
void mergeSort(vector<int>& nums, int l, int r)
{
if (l >= r) return;
// 拆
int mid = l + r >> 1;
mergeSort(nums, l, mid);
mergeSort(nums, mid + 1, r);
// 合并
vector<int> tmp;
int i = l, j = mid + 1;
while (i <= mid && j <= r)
if (nums[i] <= nums[j]) tmp.emplace_back(nums[i++]);
else tmp.emplace_back(nums[j++]);
while (i <= mid) tmp.emplace_back(nums[i++]);
while (j <= r) tmp.emplace_back(nums[j++]);
// tmp 替换
for (i = l, j = 0; i <= r; ++i, ++j) nums[i] = tmp[j];
}
整数二分算法
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
// 在右半段寻找左边界(即寻找符合性质的第一个点)
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
// 在左半段寻找右边界(即寻找不符合性质的最后一个点)
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
浮点数二分算法
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
高精度加法
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int>& A, vector<int>& B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
// 是否还有进位
if (t) C.push_back(t);
return C;
}
高精度减法
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
// 去除多余的0
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
高精度乘低精度
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
高精度除低精度
// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
一维前缀和
int n = nums.size();
// pre[i + 1] : [0, i] 范围内的所有元素和
vector<int> pre(n + 1);
for (int i = 0; i < n; ++i) {
pre[i + 1] = pre[i] + nums[i];
}
// 查找区间[left, right]的和
pre[right + 1] - pre[left]
二维前缀和
int n = nums.size(), m = nums[0].size();
// pre[i + 1][j + 1] : [0, i] 行 [0, j] 列 范围内的所有元素和
vector<vector<int>> pre(n + 1, vector<int>(m + 1));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
pre[i + 1][j + 1] = pre[i + 1][j] + pre[i][j + 1] - pre[i][j] + nums[i][j];
}
}
// 查找区间[x1, y1] 和 [x2, y2] 构成的矩形和
pre[x2 + 1][y2 + 1] + pre[x1][y1] - pre[x1][y2 + 1] - pre[x2 + 1][y1]
一维差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
求nums[i] : B[0] + B[1] + ... + B[i]
二维差分
vector<vector<int>> diff(n + 1, vector<int>(n + 1));
// 给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
diff[x1][y1] += c;
diff[x1][y2 + 1] -= c;
diff[x2 + 1][y1] -= c;
diff[x2 + 1][y2 + 1] += c;
// 对diff数组求二维前缀和即得到最终的数组
vector<vector<int>> nums(n + 1, vector<int>(n + 1));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
nums[i + 1][j + 1] = nums[i + 1][j] + nums[i][j + 1] - nums[i][j] + diff[i][j];
}
}
位运算
求n的第k位数字: n >> k & 1
返回n的最后一位1:lowbit(n) = n & -n
判断两个数是否正负相同: (a ^ b) < 0
判断x是否是2的n次方: x & (x - 1) == 0
懒标记法:如果反转某一位,可以实际不反转,而采用一个标记位,下一次再反转时相当于没反转
2.数据结构
单向链表
struct ListNode
{
int val;
ListNode* next;
};
- 获取长度
int getLength(ListNode* head) {
int ans = 0;
while (head) {
ans++;
head = head->next;
}
return ans;
}
- 删除第N个节点,N 从 1 开始, 确保 N 不大于总长度
ListNode* removeNth(ListNode* head, int n) {
ListNode dummy;
dummy.next = head;
ListNode* p = &dummy;
for (int i = 1; i < n; ++i) {
p = p->next;
}
p->next = p->next->next;
return dummy.next;
}
- 删除倒数第N个节点,N 从 1 开始, 确保 N 不大于总长度
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode dummy;
dummy.next = head;
// 快慢指针,无需确定总长度
ListNode* fast = head;
ListNode* slow = &dummy;
for (int i = 0; i < n; ++i) {
fast = fast->next;
}
while (fast) {
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;
return dummy.next;
}
- 反转链表
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* cur = head;
while (cur) {
ListNode* tmp = cur->next;
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
双向链表
struct ListNode
{
int val;
ListNode* pre;
ListNode* next;
};
栈
队列
普通队列
循环队列
单调栈 (monotonic stack)
stack<int> S;
for (int i = 0; i < n; ++i) {
while (!S.empty() && 满足) {
弹出
}
S.push(i);
}
单调队列
deque<int> dq; // 双端队列
for (int i = 0; i < n; ++i) {
while (!dq.empty() && 不满足) {
弹出队尾(队首)
}
while (!dq.empty() && 满足) {
计算
弹出队尾(队首) or 不弹出
}
dq.push_back(i); // 加入队列
}
KMP
核心是理解前缀函数
class Solution {
public:
int strStr(string haystack, string needle) {
int n = haystack.size(), m = needle.size();
if (m == 0) return 0;
vector<int> pi(m);
for (int i = 1; i < m; ++i) {
int j = pi[i - 1];
while (j > 0 && needle[i] != needle[j]) {
j = pi[j - 1];
}
if (needle[i] == needle[j]) {
j++;
}
pi[i] = j;
}
for (int i = 0, j = 0; i < n; ++i) {
while (j > 0 && haystack[i] != needle[j]) {
j = pi[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == m) {
return i - j + 1;
}
}
return -1;
}
};
扩展KMP, Z函数
vector<int> z(n);
int left = 0;
int right = 0;
for (int i = 1; i < n; ++i) {
// i 在 zbox 内, zbox 的范围 [left, right]
if (i <= right) {
z[i] = min(z[i - left], right - i + 1);
}
// 暴力匹配后面的
while (i + z[i] < n && s[z[i]] == s[i + z[i]]) {
left = i;
right = i + z[i];
z[i]++;
}
}
Trie树
核心是维护每个字符间的关系,并按照给定查找字符串的字符顺序遍历树
0-1Trie
常用于对数字进行位操作相关的查找,比如查找与给定数异或值最大的数
class Trie {
public:
struct Node {
array<Node*, 2> children{};
int cnt = 0; // 子树大小
};
// 添加 val
void insert(int val) {
Node* cur = root;
for (int i = HIGH_BIT; i >= 0; i--) {
int bit = (val >> i) & 1;
if (cur->children[bit] == nullptr) {
cur->children[bit] = new Node();
}
cur = cur->children[bit];
cur->cnt++; // 维护子树大小
}
}
// 删除 val,但不删除节点
// 要求 val 必须在 trie 中
void remove(int val) {
Node* cur = root;
for (int i = HIGH_BIT; i >= 0; i--) {
cur = cur->children[(val >> i) & 1];
cur->cnt--; // 维护子树大小
}
}
// 返回 val 与 trie 中一个元素的最大异或和
// 要求 trie 不能为空
int max_xor(int val) {
Node* cur = root;
int ans = 0;
for (int i = HIGH_BIT; i >= 0; i--) {
int bit = (val >> i) & 1;
// 如果 cur.children[bit^1].cnt == 0,视作空节点
if (cur->children[bit ^ 1] && cur->children[bit ^ 1]->cnt) {
ans |= 1 << i;
bit ^= 1;
}
cur = cur->children[bit];
}
return ans;
}
private:
static constexpr int HIGH_BIT = 19;
Node* root = new Node();
};
并查集
堆
堆是完全二叉树,push时从子节点向上更新堆顶;pop时swap堆顶堆尾,再向下找更小的值更新堆顶。
应用场景:
- 多路归并,按照优先级排序,需要先将一路加入到priority_queue中,再开始多路的访问 -> 373. 查找和最小的 K 对数字
template<class T, class Cmp>
class Heap
{
public:
void push(const T& v) {
m_data.emplace_back(v);
int child = m_data.size() - 1;
while (child > 0 && (child - 1) / 2 >= 0) {
int parent = (child - 1) / 2;
if (m_cmp(m_data[parent], m_data[child])) {
swap(m_data[child], m_data[parent]);
}
child = parent;
}
}
void pop() {
swap(m_data.front(), m_data.back());
m_data.pop_back();
// update top
int parent = 0;
while (2 * parent + 1 < m_data.size()) {
int child = 2 * parent + 1;
if (child + 1 < m_data.size() && m_cmp(m_data[child], m_data[child + 1])) {
child++;
}
if (m_cmp(m_data[parent], m_data[child])) {
swap(m_data[parent], m_data[child]);
}
parent = child;
}
}
T top() {
return m_data[0];
}
size_t size() {
return m_data.size();
}
private:
vector<T> m_data;
Cmp m_cmp;
};
一般哈希
拉链法
int N = 10007;
vector<list<int>> data(N);
// 找位置,插入
void add(int x) {
int index = (x % N + N) % N;
for (const auto& i : data[index]) {
if (i == x) return;
}
data[index].push_back(x);
}
bool find(int x) {
int index = (x % N + N) % N;
for (const auto& i : data[index]) {
if (i == x) return true;
}
return false;
}
开放寻址法
int N = 10007;
vector<int> data(N);
// 找位置,插入
void add(int x) {
int index = find(x);
data[index] = x;
}
// 如果x在哈希表中,返回x的下标;如果x不在哈希表中,返回x应该插入的位置
int find(int x) {
int index = (x % N + N) % N;
// 这里假定哈希的容量在N以内(否则就要考虑扩容)
while (data[index] != 0 && data[index] != x) {
index++;
if (index == N) {
index = 0;
}
}
return index;
}
字符串哈希
核心思想:将字符串看成P进制数,P的经验值是131或13331,取这两个值的冲突概率低
小技巧:取模的数用2^64,这样直接用unsigned long long存储,溢出的结果就是取模的结果
// 初始化
constexpr int P = 13331;
int n = str.size();
vector<unsigned long long> h(n + 1), p(n + 1); // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
p[0] = 1;
for (int i = 0; i < n; ++i) {
h[i + 1] = h[i] * P + str[i];
p[i + 1] = p[i] * P;
}
// 计算字串 str[l ~ r] 的哈希值
unsigned long long get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}
树状数组(Binary Indexed Trees)
树状数组是一种支持 单点修改 和 区间查询 的,代码量小的数据结构
为方便树状数组的索引从1开始
用处
一般配合离散化使用
// 维护前缀最大值
class BIT {
vector<long long> tree;
public:
BIT(int n) : tree(n, LLONG_MIN) {}
void update(int i, long long val) {
while (i < tree.size()) {
tree[i] = max(tree[i], val);
i += lowbit(i);
}
}
long long pre_max(int i) {
long long res = LLONG_MIN;
while (i > 0) {
res = max(res, tree[i]);
i -= lowbit(i);
}
return res;
}
int lowbit(int x) {
return x & -x;
}
};
3.搜索与图论
树与图的存储
树是一种特殊的图,与图的存储方式相同。
对于无向图中的边ab,存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。
- 邻接矩阵 g[a][b] 存储边a->b
- 邻接表 对于每个点k,开一个单链表,存储k所有可以走到的点
树与图的遍历
时间复杂度 O(n+m), n表示点数,m表示边数
dfs
int dfs(int u)
{
st[u] = true; // st[u] 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) dfs(j);
}
}
bfs
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size()) {
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (!st[j]) {
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
树上问题
二叉树的前中后序遍历
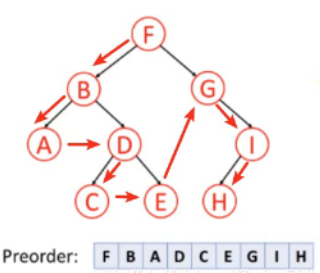
// 前序(中、左、右)
vector<int> preorderTraversal(TreeNode* root) {
if (!root) return {};
stack<TreeNode*> s;
TreeNode* p = root;
vector<int> ans;
while (!s.empty() || p) {
while (p) {
ans.emplace_back(p->val);
s.push(p->right);
p = p->left;
}
p = s.top();
s.pop();
}
return ans;
}
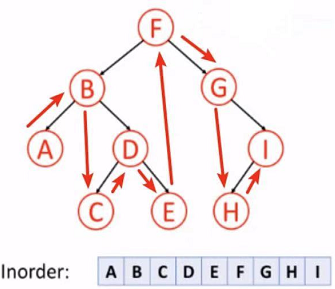
// 中序(左、中、右)
vector<int> inorderTraversal(TreeNode* root) {
if (!root) return {};
vector<int> ans;
stack<TreeNode*> s;
TreeNode* p = root;
while (!s.empty() || p) {
while (p) {
s.push(p);
p = p->left;
}
auto cur = s.top();
s.pop();
ans.emplace_back(cur->val);
p = cur->right;
}
return ans;
}
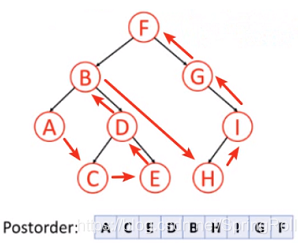
// 后序(左、右、中)
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> s;
TreeNode* pre = nullptr;
while (!s.empty() || root) {
while (root) {
s.push(root);
root = root->left;
}
auto cur = s.top();
s.pop();
// 当前节点的右节点已经遍历过
if (cur->right == nullptr || cur->right == pre) {
ans.emplace_back(cur->val);
pre = cur;
}
// 未遍历过则要遍历右节点
else {
s.push(cur);
root = cur->right;
}
}
return ans;
}
求每个节点的树高
unordered_map<TreeNode*, int> nodeHeight;
function<int(TreeNode*)> getHeight = [&](TreeNode* node) {
if (!node) return 0;
int left = getHeight(node->left);
int right = getHeight(node->right);
return nodeHeight[node] = max(left, right) + 1;
};
getHeight(root);
树的直径
记录任意节点的最远节点距离d1和次远节点距离d2,则树的直径是所有(d1 + d2)的最大值
int n, d = 0;
int d1[N], d2[N];
vector<int> E[N];
void dfs(int u, int fa) {
d1[u] = d2[u] = 0;
for (int v : E[u]) {
if (v == fa) continue;
dfs(v, u);
int t = d1[v] + 1;
if (t > d1[u])
d2[u] = d1[u], d1[u] = t;
else if (t > d2[u])
d2[u] = t;
}
d = max(d, d1[u] + d2[u]);
}
树上倍增
倍增是一种思想,例如要得到第15(1111)个数,即是第 8(1000) + 4(100) + 2(10) + 1(1) 个,因此只要不同的个数之间存在关联,就能建立这种关系
class TreeAncestor {
public:
TreeAncestor(int n, vector<vector<int>>& edges) {
int m = binarySize(n);
dp.resize(n, vector<int>(m, -1));
depth.resize(n);
vector<vector<int>> graph(n);
for (const auto& e : edges) {
int a = e[0], b = e[1];
graph[a].push_back(b);
graph[b].push_back(a);
}
function<void(int, int)> dfs = [&](int cur, int parent) {
dp[cur][0] = parent;
for (const auto& next : graph[cur]) {
if (next == parent) continue;
depth[next] = depth[cur] + 1;
dfs(next, cur);
}
};
dfs(0, -1);
for (int i = 0; i < m - 1; ++i) {
for (int x = 0; x < n; ++x) {
if (int p = dp[x][i]; p != -1) {
dp[x][i + 1] = dp[p][i];
}
}
}
}
int getKthAncestor(int node, int k) {
int m = binarySize(k);
for (int i = 0; i < m; ++i) {
if (k >> i & 1) {
node = dp[node][i];
if (node < 0) break;
}
}
return node;
}
int binarySize(int num) {
for (int i = 31; i >= 0; --i) {
if (num >> i & 1) return i + 1;
}
return 1;
}
// 返回 x 和 y 的最近公共祖先(节点编号从 0 开始)
int getLca(int x, int y) {
if (depth[x] > depth[y])
swap(x, y);
// 使 y 和 x 在同一深度
y = getKthAncestor(y, depth[y] - depth[x]);
if (y == x)
return x;
for (int i = dp[x].size() - 1; i >= 0; i--) {
int px = dp[x][i], py = dp[y][i];
if (px != py) {
x = px;
y = py;
}
}
return dp[x][0];
}
private:
vector<vector<int>> dp;
vector<int> depth;
};
拓扑排序
最短路
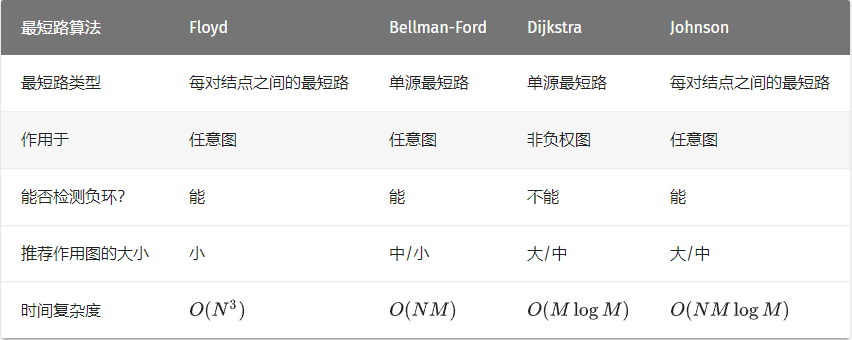
这里有个思想,反图,比如求A、B到达C的最短路径,一定是 A->mid->C, B->mid->C, 求 mid->C 需要反向建图,见得到要求路径的最小带权子图
朴素dijkstra
时间复杂度 O(n2 + m) n表示点数,m表示边数
struct edge {
int v, w;
};
vector<vector<edge>> graph(n);
vector<int> dis(n, inf);
vector<bool> vis(n);
dis[start] = 0;
// 遍历n次
for (int i = 0; i < n; ++i) {
// 找最近的节点
int cur= 0, minDis = inf;
for (int j = 0; j < n; ++j) {
if (!vis[j] && dis[j] < minDis) {
cur= j;
minDis = dis[j];
}
}
vis[cur] = true;
// 更新其他临点
for (auto& e : graph[cur]) {
int next = e.v, w = e.w;
if (dis[next] > dis[cur] + w) {
dis[next] = dis[cur] + w;
}
}
}
堆优化dijkstra
时间复杂度 O(mlogm) n表示点数,m表示边数
struct edge {
int v, w;
};
struct node {
int dis, u;
bool operator>(const node& a) const { return dis > a.dis; }
};
vector<vector<edge>> graph(n);
vector<int> dis(n, inf);
vector<bool> vis(n);
priority_queue<node, vector<node>, greater<node>> pq;
dis[start] = 0;
pq.push({0, start});
while (!pq.empty()) {
auto cur = pq.top().u;
pq.pop();
if (vis[cur]) continue;
vis[cur] = true;
// 更新其他临点
for (auto& e : graph[cur]) {
int next = e.v, w = e.w;
if (dis[next] > dis[cur] + w) {
dis[next] = dis[cur] + w;
pq.push({dis[next], next});
}
}
}
floyd
暴力算法,时间复杂度 O(n3) n表示点数,不过可以求出所有两两节点间的最短路
vector<vector<int>> dis(n, vector<int>(n, inf));
// 算法结束后,dis[a][b]表示a到b的最短距离
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
内向基环树
二分图Bipartite graph
定义:节点由两个集合组成,且集合内部没有边的图
性质:二分图不存在长度为奇数的环
染色法判别二分图
核心是有一个color列表,存放节点的染色结果,未染色为0,1代表染成一种颜色,2代表染成另一种颜色。
如果父节点为染色结果为1,那么如果子节点未染色,将子节点的染色结果设置为2.
如果子节点染色了,判断染色和父节点是否一致,如果一致,则不是二分图
vector<vector<int>> graph(n);
vector<int> color(n);
queue<int> q;
for (int i = 0; i < n; ++i) {
if (color[i] == 0) {
q.push(i);
color[i] = 1;
}
while (!q.empty()) {
auto cur = q.front();
q.pop();
int nextColor = color[cur] == 1 ? 2 : 1;
for (const auto& next : graph[cur]) {
if (color[next] == 0) {
q.push(next);
color[next] = nextColor;
}
else if (color[next] == color[cur]) {
return false;
}
}
}
}
return true;
数学知识
阶乘
阶乘后0的个数
// 2 * 5 = 10 产生一个0,所以相当于判断有多少组(2, 5),相当于求5的个数
int trailingZeroes(int n) {
int ans = 0;
while (n) {
n /= 5;
ans += n;
}
return ans;
}
质数
试除法判定质数
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
试除法分解质因数
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}
朴素筛法求素数
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
线性筛法求素数
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
约数
试除法求所有约数
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}
约数个数之和
如果 N = p1c1 * p2c2 * ... *pkck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p10 + p11 + ... + p1c1) * ... * (pk0 + pk1 + ... + pkck)
欧几里得算法(辗转相除法)
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
扩展欧几里得算法
// 求x, y,使得ax + by = gcd(a, b)
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1; y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= (a/b) * x;
return d;
}
快速幂
求 xk
long long fastPow(long long x, int k) {
long long ans = 1;
while (k) {
if (k % 2 == 1) {
ans *= x;
}
x *= x;
k /= 2;
}
return ans;
}
乘法逆元
(a mod p) * x = 1, 则称 x 为 a 模 p 的乘法逆元
乘法逆元的作用是把除法变为乘法,比如求 (a / b) mod p 的值,而 a 和 b 都是计算量很大的表达式,这样乘法会溢出,除法操作难以实现,可以转换为:
- a * b-1 mod p
- 先求 a mod p
- 求乘法逆元 b-1
- 上述两个结果相乘再模 p 即得到所需结果
快速幂法(需要p为素数)
// 求 x 的 k 次方模modN
int qpow(long long x, int k, int modN) {
int ans = 1;
for (; k; k >>= 1) {
if (k & 1) ans = (x * ans) % modN;
x = (x * x) % modN;
}
return ans;
}
// 费马小定理,https://oi-wiki.org/math/number-theory/fermat/
// b^-1 = qpow(a, p - 2, p);
扩展欧几里得法(需要 gcd(a, p) == 1)
a * b mod p = 1 -> ab - kp = 1
令 x = b, y = -k, 可得 ax + py = 1 = gcd(a, p), 按照扩展欧几里得法求出 x, y, 那么x就是乘法逆元
void exgcd(int a, int b, int& x, int& y) {
if (b == 0) {
x = 1, y = 0;
return;
}
exgcd(b, a % b, y, x);
y -= a / b * x;
}
组合数
递归法(O(n^2))
// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
c[i][0] = 1;
for (int j = 1; j <= i; j ++ )
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
通过预处理逆元的方式
// 首先预处理出所有阶乘取模的余数fact[N],以及所有阶乘取模的逆元infact[N]
// 如果取模的数是质数,可以用费马小定理求逆元
// 求 x 的 k 次方模modN
int qpow(long long x, int k, int modN) {
int ans = 1;
for (; k; k >>= 1) {
if (k & 1) ans = (x * ans) % modN;
x = (x * x) % modN;
}
return ans;
}
// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qpow(i, mod - 2, mod) % mod;
}
4.动态规划
背包问题
有 n 个物品和一个容量为 W 的背包,每个物品有重量 wi 和价值 vi 两种属性,要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。
0-1背包
每个物品只有取和不取两个状态
for (int i = 1; i <= n; ++i) {
// 倒序,因为 j >= j - w[i]。如果正序,则求 j 时 j - w[i] 已经更新过(意味着更新为dp[i][j - w[i]] 而不是原来的 dp[i - 1][j - w[i]])
for (int j = W; j >= w[i]; --j) {
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
完全背包
每个物品可以取无限次
for (int i = 1; i <= n; ++i) {
// 正序
for (int j = w[i]; j <= W; ++j) {
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
多重背包
多重背包也是 0-1 背包的一个变式。与 0-1 背包的区别在于每种物品有 ki 个,而非一个。
// 把**重量为w[i], 每个取k[i]次**转变为**k[i]个重量为w[i], 每个取1次**, 这就是0-1背包问题
for (int i = 1; i <= n; ++i) {
for (int j = W; j >= w[i]; --j) {
// 以上为01背包,然后再遍历个数
for (int k = 1; k <= nums[i] && k * w[i] <= j; ++k) {
dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
}
}
}
二进制优化
在上面的做法中,存在大量重复计算,比如:
k个重量为w[i],分别编号为w'[i], w'[i + 1], ..., w'[i + k - 1], 此时我想再拿2个出来,取w'[i]和w'[i + 1], 与取w'[i + 1]和w'[i + 2] 有区别吗?他们都是同样的重量呀
所以我们把k个变为 1 + 1 + 1 + 1 + ... 本身就重复太多啦
为什么不把k个,变为 1 + 2 + 4 + 8 + ... 呢?
vector<int> weight;
vector<int> value;
for (int i = 0; i < n; ++i) {
// 对k进行拆分
int k = nums[i];
int cnt = 1;
while (k - cnt > 0) {
k -= cnt;
weight.push_back(w[i] * cnt);
value.push_back(v[i] * cnt);
cnt *= 2;
}
weight.push_back(w[i] * k);
value.push_back(v[i] * k);
}
// 01背包
for (int i = 0; i < weight.size(); ++i) {
for (int j = W; j >= weight[i]; --j) {
dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
}
}
滚动数组优化
区间dp
// 枚举区间长度
for (int k = 2; k < size; ++k) {
// 枚举左右端点
for (int i = 0, j = k; j < size; ++i, ++j) {
dp[i][j] = INT_MAX;
// 枚举分割点
for (int x = i + 1; x < j; ++x) {
dp[i][j] = min(dp[i][j], dp[i][x] + dp[x][j] + 消耗);
}
}
}
计数类dp
数位统计dp
dp[i][j]表示当前在第i位,前面维护了一个为j的值,且后面的位数可以随便选时的数字个数
定义函数f(i, mask, isLimit, isNum)表示构造从左往右第i位及其之后数位合法的方案数,其余参数的含义为:
- mask表示前面选过的数字集合,换句话说,第i位数字不能在mask中
- isLimit表示当前是否受到了约束,若为真,则第i位填入的数字至多为s[i],否则可以是9。如果在受到约束的情况下填入9,则后面还会被约束
- isNum表示前i位是否填了数字,若为真,则填入的数字可以是从0开始,否则不能有前导0,即可以跳过当前数字或者从1开始
注意mask是可以变通的,比如
- 2719. 统计整数数目, mask 是当前的数字和
则递归入口为:f(0, 0, true, false)
string nstr; // 给定数字的字符串形式
int n = nstr.size(); // 位数
int m = 1 << 10; // 0 - 9 的mask
vector<vector<int>> dp(n, vector<int>(m, -1));
function<int(int, int, bool, bool)> dfs = [&](int index, int mask, bool isLimit, bool isNum) {
// 到头
if (index == n) return ...;
// 已缓存
if (!isLimit && dp[index][mask] >= 0) {
return dp[index][mask];
}
int ans = 0;
// 是否可以跳过
if (!isNum) {
ans += dfs(index + 1, mask, false, false);
}
// 确定枚举数字范围,最多[0, 9]
int left = 1 - isNum;
int right = isLimit ? nstr[index] - '0' : 9;
for (int i = left; i <= right; ++i) {
// 不在mask中
if (mask >> i & 1) continue;
ans += dfs(index + 1, mask | (1 << i), isLimit && i == right, true);
}
// 缓存
if (!isLimit) {
dp[index][mask] = ans;
}
return ans;
};
状态压缩dp
//集合A、B,元素c --> int A,B c = 0 ~ 31
//A中插入c
A |= (1<<c)
//A中去除c
A &= ~(1<<c)
//A中去除c, c 一定在A中
A ^= (1<<c)
//A B 合并
A | B
//判断B是不是A的子集
return (A&B) == B
//判断c在不在A里
return A & (1<<c)
//lowbit
return x & (-x);
//枚举A的全部子集
for(int i = A; i; i = (i-1) & A)
{
//do something
}
// 将一个数的最低位到最高位(最高位为从高到低第一个1)全部置1
int num = 0b10110;
int mask = 0;
while (mask < num)
{
mask = (mask << 1) + 1;
}
树形dp
换根dp
这类问题常见形式:n个节点组成一个无环图,选择任意节点作为根都可以得到一棵树,求这n个节点分别作为根时的(xxx的最大值、最小值...)
解法一般分为两步:
- 求出以0为根的状态
- 换根,假设 i,j 为一条边的两个端点,且i的状态已知,求j的状态
我们以LC310.最小高度树为例:
- 记录以0为根时,以每个节点为根的子树的最大高度height
- 换根,假设当前根节点为r,以u为根的子树高度为heightr[u],则当把根由r换为u后,heightu[r] = max(heightr[ai]) + 1,heightu[u] = max(heightr[u], heightu[r] + 1)
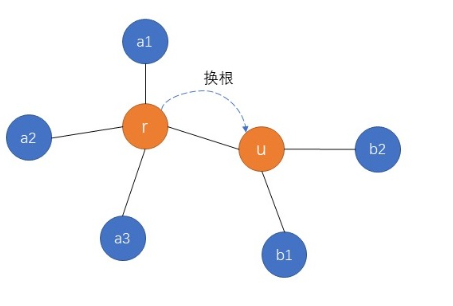
- 最后求出所有的最大的heighti[i]即可
class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
// construct graph
vector<vector<int>> graph(n);
for (const auto& edge : edges) {
int a = edge[0], b = edge[1];
graph[a].emplace_back(b);
graph[b].emplace_back(a);
}
// 0 as root, cal all height
vector<int> height_0(n);
function<int(int, int)> dfs1 = [&](int cur, int parent) {
int h = 0;
for (int next : graph[cur]) {
if (next == parent) continue;
h = max(h, dfs1(next, cur));
}
height_0[cur] = h + 1;
return height_0[cur];
};
dfs1(0, -1);
// 换根dfs
vector<int> height_i(n);
function<void(int, int)> dfs2 = [&](int cur, int parent) {
// 预处理与cur相连的节点的第一大和第二大值
int h1 = 0, h2 = 0;
for (int next : graph[cur]) {
int h = height_0[next];
if (h > h1) {
h2 = h1;
h1 = h;
}
else if (h > h2) {
h2 = h;
}
}
// 记录以cur为根的树高
height_i[cur] = h1 + 1;
// 换根
for (int next : graph[cur]) {
if (next == parent) continue;
int h = height_0[next] == h1 ? h2 : h1;
height_0[cur] = h + 1;
dfs2(next, cur);
}
};
dfs2(0, -1);
vector<int> ans;
int maxh = n;
for (int i = 0; i < n; ++i) {
if (height_i[i] < maxh) {
maxh = height_i[i];
ans.clear();
ans.emplace_back(i);
}
else if (height_i[i] == maxh) {
ans.emplace_back(i);
}
}
return ans;
}
};
记忆化搜索
前后缀分解DP
// 数组 nums[n], 在中间任选一个位置 i, 求左侧和右侧的和的最值
// 相当于两个dp,pre[i]为左侧最值, suf[i]为右侧最值, 最终返回 pre[i] + suf[i] 的最值
计算几何
距离
比如 曼哈顿距离 和 切比雪夫距离 的转化


