约瑟夫环问题

相关题目

剑指 Offer 62. 圆圈中最后剩下的数字
5727. 找出游戏的获胜者

是什么

• n个人（1 2 3 …… n）
• 每次往后数k(k>=1)个，剔除这个数，注意数k个数的时候包含起点
• 循环剔除，直到剩下一人
  

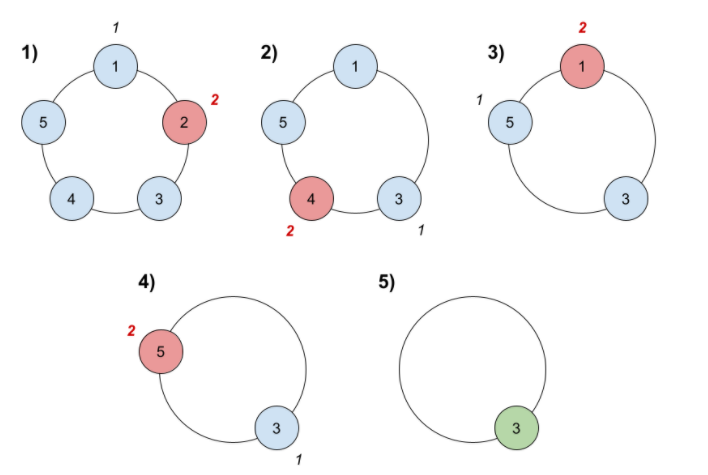
怎么算

我们将上述问题建模为函数 f(n, k)，该函数的返回值为最终留下的元素的序号。即：f(n, k) = y

我们假设f(n-1, k) = x，然后来找一找f(n, k)和f(n-1, k)到底啥关系。

• f(n, k) = y 从n到n-1, 只需要剔除掉一个数，这个数的下标是 (k-1) % n，此时序列由[0, 1, 2, ……, n-1]变为[0, (k-1) % n) 和 （(k-1) % n, n-1]两段
• 相当于此时的n-1长度序列变为((k-1) % n, n-1, 0, (k-1) % n))，考虑到有可能剔除的是最后一个数，所以最终范围变成以((k-1)%n + 1)%(n-1)为起始点的长为n-1的序列
• f(n-1, k) = x的序列是从0开始长为n-1的序列，注意到没？相当于和上面的序列((k-1) % n, n-1, 0, (k-1) % n))左移k个
• 最后保留的元素，如果在长n序列保留，必定在长n-1序列保留，只是有了一个偏移k。否则这个数都被你剔除掉了你还咋保留嘞？
• 即y = (x + k) % n --> f(n, k) = (f(n-1, k) + k) % n

代码

//递归
int f(int n, int k){
  if(n == 1) return 0;
  return (f(n-1, k) + k) % n;
}

//迭代
int f(int n, int k){
  int ans = 0;
  for(int i = 2; i <= n; ++i){
    ans = (ans + k) % i;
  }
  return ans;
}